Difference between revisions of "Eilenberg-MacLane space"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Eilenberg–MacLane space to Eilenberg-MacLane space: ascii title) |
(No difference)
| |
Revision as of 18:51, 24 March 2012
A space, denoted by 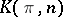 , representing the functor
, representing the functor 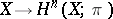 , where
, where  is a non-negative number,
is a non-negative number, 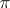 is a group which is commutative for
is a group which is commutative for 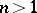 and
and 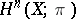 is the
is the  -dimensional cohomology group of a cellular space
-dimensional cohomology group of a cellular space 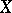 with coefficients in
with coefficients in 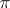 . It exists for any such
. It exists for any such  and
and 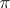 .
.
The Eilenberg–MacLane space 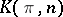 can also be characterized by the condition:
can also be characterized by the condition: 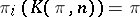 for
for 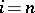 and
and 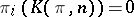 for
for 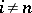 , where
, where 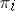 is the
is the 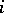 -th homotopy group. Thus,
-th homotopy group. Thus, 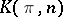 is uniquely defined up to a weak homotopy equivalence. An arbitrary topological space can, up to a weak homotopy equivalence, be decomposed into a twisted product of Eilenberg–MacLane spaces (see Postnikov system). The cohomology groups of
is uniquely defined up to a weak homotopy equivalence. An arbitrary topological space can, up to a weak homotopy equivalence, be decomposed into a twisted product of Eilenberg–MacLane spaces (see Postnikov system). The cohomology groups of 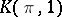 coincide with those of
coincide with those of 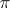 . Eilenberg–MacLane spaces were introduced by S. Eilenberg and S. MacLane .
. Eilenberg–MacLane spaces were introduced by S. Eilenberg and S. MacLane .
References
| [1a] | S. Eilenberg, S. MacLane, "Relations between homology and homotopy groups of spaces" Ann. of Math. , 46 (1945) pp. 480–509 |
| [1b] | S. Eilenberg, S. MacLane, "Relations between homology and homotopy groups of spaces. II" Ann. of Math. , 51 (1950) pp. 514–533 |
| [2] | R.E. Mosher, M.C. Tangora, "Cohomology operations and applications in homotopy theory" , Harper & Row (1968) |
| [4] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
Eilenberg-MacLane space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Eilenberg-MacLane_space&oldid=16373