Eichler cohomology
In [a2], M. Eichler conceived the "Eichler cohomology theory" (but not the designation) while studying "generalized Abelian integrals" (now called "Eichler integrals" ; see below).
The setting for this theory is that of automorphic forms, with multiplier system, on a discrete group 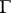 of fractional-linear transformations (equivalently, of
of fractional-linear transformations (equivalently, of 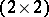 -matrices; cf. also Automorphic form; Fractional-linear mapping). One may assume that
-matrices; cf. also Automorphic form; Fractional-linear mapping). One may assume that 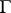 consists of real fractional-linear transformations, that is, that
consists of real fractional-linear transformations, that is, that 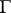 fixes
fixes 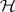 , the upper half-plane. A fundamental region,
, the upper half-plane. A fundamental region, 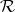 , of
, of 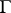 is required to have finite hyperbolic area; this is equivalent to the two conditions (taken jointly):
is required to have finite hyperbolic area; this is equivalent to the two conditions (taken jointly):
i) 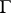 is finitely generated;
is finitely generated;
ii) each real point 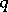 of
of  is a parabolic point (a cusp) of
is a parabolic point (a cusp) of 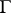 , that is, it is fixed by a cyclic subgroup
, that is, it is fixed by a cyclic subgroup 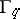 of
of 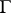 with parabolic generator.
with parabolic generator.
Let 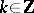 and let
and let  be a multiplier system in weight
be a multiplier system in weight 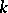 with respect to
with respect to 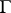 . Since
. Since 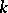 is integral, this means simply that
is integral, this means simply that 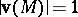 for all
for all 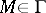 , and
, and  is multiplicative:
is multiplicative:
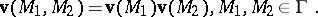 | (a1) |
For 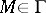 and
and 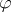 a function on
a function on 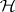 , define the slash operator
, define the slash operator
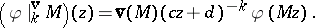 | (a2) |
In this notation, the characteristic transformation law satisfied by an automorphic form 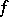 on
on 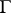 of weight
of weight 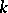 and multiplier system
and multiplier system  can be written
can be written
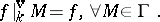 | (a3) |
Let 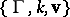 denote the vector space of automorphic forms on
denote the vector space of automorphic forms on 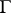 of weight
of weight 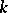 and multiplier system
and multiplier system  , the collection of
, the collection of 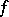 satisfying (a3) and that are holomorphic on
satisfying (a3) and that are holomorphic on 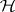 and meromorphic at each parabolic cusp of
and meromorphic at each parabolic cusp of 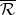 (in the usual local variable, cf. also Analytic function; Meromorphic function). One says that
(in the usual local variable, cf. also Analytic function; Meromorphic function). One says that 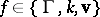 is an entire automorphic form if
is an entire automorphic form if 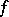 is holomorphic at each parabolic cusp. An entire automorphic form
is holomorphic at each parabolic cusp. An entire automorphic form 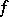 is called a cusp form if
is called a cusp form if 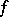 vanishes at each parabolic cusp. As usual,
vanishes at each parabolic cusp. As usual, 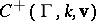 denotes the space of entire automorphic forms and
denotes the space of entire automorphic forms and 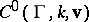 denotes the subspace of cusp forms. For groups
denotes the subspace of cusp forms. For groups 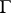 of the kind considered here, a suitable version of the Riemann–Roch theorem shows that
of the kind considered here, a suitable version of the Riemann–Roch theorem shows that 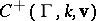 has finite dimension over
has finite dimension over 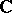 .
.
To describe the genesis of Eichler cohomology it is helpful to introduce the Bol identity [a1]:
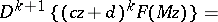 | (a4) |
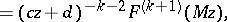 |
where  ,
, 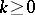 ,
,  is any fractional-linear transformation of determinant
is any fractional-linear transformation of determinant  , and
, and 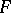 is a function with
is a function with 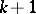 derivatives ((a4) is easily derived from the Cauchy integral formula, cf. Cauchy integral theorem, or proved by induction on
derivatives ((a4) is easily derived from the Cauchy integral formula, cf. Cauchy integral theorem, or proved by induction on 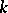 ). As a consequence of (a4), if
). As a consequence of (a4), if 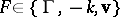 , then
, then 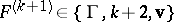 .
.
There is a second consequence of (a4), more directly relevant to the case under consideration: if 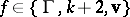 and
and 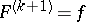 (for example,
(for example, 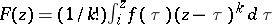 ), then
), then 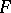 satisfies
satisfies
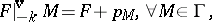 | (a5) |
where 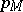 is a polynomial in
is a polynomial in  of degree at most
of degree at most 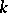 .
. 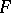 is called an Eichler integral of weight
is called an Eichler integral of weight 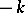 and multiplier system
and multiplier system  , with respect to
, with respect to 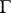 , and with period polynomials
, and with period polynomials 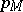 ,
, 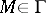 . Eichler integrals generalize the classical Abelian integrals (cf. Abelian integral), which occur as the case
. Eichler integrals generalize the classical Abelian integrals (cf. Abelian integral), which occur as the case 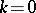 ,
, 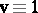 . As an immediate consequence of (a5),
. As an immediate consequence of (a5),  satisfies the cocycle condition
satisfies the cocycle condition
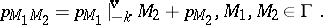 | (a6) |
Consider the cocycle condition for  in the space
in the space  of polynomials of degree at most
of polynomials of degree at most  . A collection of polynomials
. A collection of polynomials 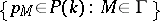 satisfying (a6) is called a cocycle in
satisfying (a6) is called a cocycle in 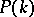 . A coboundary in
. A coboundary in 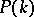 is a collection
is a collection 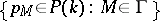 such that
such that
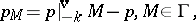 | (a7) |
with a fixed polynomial 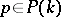 . Note that
. Note that 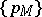 defined by (a7) satisfies (a6). The Eichler cohomology group
defined by (a7) satisfies (a6). The Eichler cohomology group 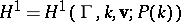 is now defined to be the quotient space: cocycles in
is now defined to be the quotient space: cocycles in 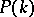 modulo coboundaries in
modulo coboundaries in  .
.
To state Eichler's cohomology theorem of [a2] one must introduce the notion of a "parabolic cocycle" . Let 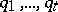 be the (necessarily finite) set of inequivalent parabolic cusps in
be the (necessarily finite) set of inequivalent parabolic cusps in 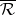 . For
. For 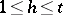 , let
, let  be the stabilizer of
be the stabilizer of 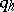 in
in 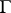 with parabolic generator
with parabolic generator 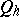 (cf. also Stabilizer). One says that the cocycle
(cf. also Stabilizer). One says that the cocycle 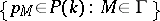 is parabolic if the following holds: For each
is parabolic if the following holds: For each  ,
, 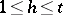 , there exists a
, there exists a 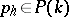 such that
such that 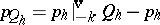 .
.
Coboundaries are of course parabolic cocycles, so one may form the quotient group: parabolic cocycles in 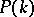 modulo coboundaries in
modulo coboundaries in 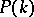 . This is a subgroup of
. This is a subgroup of 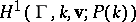 , called the parabolic Eichler cohomology group and denoted by
, called the parabolic Eichler cohomology group and denoted by 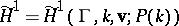 .
.
Eichler's theorem [a2], p. 283, states: The vector spaces 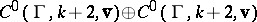 and
and 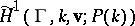 are isomorphic under a canonical mapping.
are isomorphic under a canonical mapping.
The discussion above, leading to (a6), shows how to associate a unique element 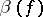 of
of 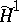 to
to 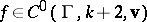 , by forming a
, by forming a 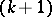 -fold anti-derivative of
-fold anti-derivative of 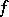 . The key to the proof of Eichler's theorem lies in the construction of a suitable mapping
. The key to the proof of Eichler's theorem lies in the construction of a suitable mapping 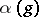 from
from 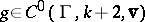 to
to  . Eichler accomplishes this by attaching to
. Eichler accomplishes this by attaching to 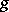 an element
an element  of
of 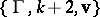 with poles in
with poles in 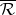 , and then passing to the cocycle of period polynomials of a
, and then passing to the cocycle of period polynomials of a 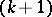 -fold anti-derivative of
-fold anti-derivative of 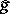 . The mapping
. The mapping 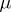 from
from 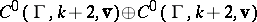 to
to 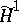 is then defined by means of
is then defined by means of 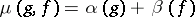 . The proof that
. The proof that 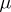 is one-to-one follows from Eichler's generalization of the Riemann period relation for Abelian integrals to the setting of Eichler integrals.
is one-to-one follows from Eichler's generalization of the Riemann period relation for Abelian integrals to the setting of Eichler integrals.
The proof can be completed by showing that 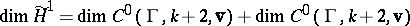 . The essence of Eichler's theorem is that every parabolic cocycle can be realized as the system of period polynomials of some unique Eichler integral of weight
. The essence of Eichler's theorem is that every parabolic cocycle can be realized as the system of period polynomials of some unique Eichler integral of weight 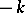 and multiplier system
and multiplier system  , with respect to
, with respect to 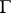 .
.
R.C. Gunning [a3] has proved a related result, from which Eichler's theorem follows as a corollary: The vector spaces 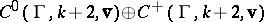 and
and 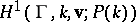 are isomorphic under the mapping of Eichler's theorem.
are isomorphic under the mapping of Eichler's theorem.
Proving Gunning 's theorem first and then deriving Eichler's theorem from it has the advantage that the calculation of 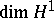 is substantially easier than that of
is substantially easier than that of 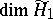 ; this, because in
; this, because in 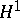 there is no restriction on the elements of
there is no restriction on the elements of 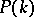 associated to the parabolic generators
associated to the parabolic generators 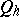 ,
, 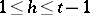 .
.
There are various proofs of Gunning 's theorem and its corollary, in addition to those in [a2], [a3]. See, for example, [a4], [a11], [a14]. (G. Shimura [a14] has refined Eichler's theorem by working over the real rather than the complex field.) In [a6], Chap. 5, [a7], [a8], and [a13], analogous results are proved for the more general situation in which 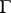 is a finitely generated Kleinian group. I. Kra has made further contributions to this case ([a9], [a10]).
is a finitely generated Kleinian group. I. Kra has made further contributions to this case ([a9], [a10]).
The literature contains several results describing the cohomology groups  and
and 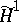 that arise when the space of polynomials
that arise when the space of polynomials 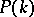 is replaced by a larger space of analytic functions [a3], Thm. 3, [a5], Thms. 1; 2, [a7], Thm. 5. Gunning [a3], Thms. 4; 5, discusses
is replaced by a larger space of analytic functions [a3], Thm. 3, [a5], Thms. 1; 2, [a7], Thm. 5. Gunning [a3], Thms. 4; 5, discusses 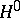 and
and 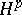 , for
, for 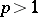 , as well as
, as well as 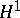 . For an overview see [a5].
. For an overview see [a5].
References
| [a1] | G. Bol, "Invarianten linearer Differentialgleichungen" Abh. Math. Sem. Univ. Hamburg , 16 : 3–4 (1949) pp. 1–28 |
| [a2] | M. Eichler, "Eine Verallgemeinerung der Abelschen Integrale" Math. Z. , 67 (1957) pp. 267–298 |
| [a3] | R.C. Gunning, "The Eichler cohomology groups and automorphic forms" Trans. Amer. Math. Soc. , 100 (1961) pp. 44–62 |
| [a4] | S.Y. Hussemi, M.I. Knopp, "Eichler cohomology and automorphic forms" Illinois J. Math. , 15 (1971) pp. 565–577 |
| [a5] | M.I. Knopp, "Some new results on the Eichler cohomology of automorphic forms" Bull. Amer. Math. Soc. , 80 (1974) pp. 607–632 |
| [a6] | I. Kra, "Automorphic forms and Kleinian groups" , Benjamin (1972) |
| [a7] | I. Kra, "On cohomology of Kleinian groups" Ann. of Math. , 89 : 2 (1969) pp. 533–556 |
| [a8] | I. Kra, "On cohomology of Kleinian groups - II" Ann. of Math. , 90 : 2 (1969) pp. 576–590 |
| [a9] | I. Kra, "On cohomology of Kleinian groups - III" Acta Math. , 127 (1971) pp. 23–40 |
| [a10] | I. Kra, "On cohomology of Kleinian groups - IV" J. d'Anal. Math. , 43 (1983-84) pp. 51–87 |
| [a11] | J. Lehner, "Automorphic Integrals with preassigned period polynomials and the Eichler cohomology" A.O.L. Atkin (ed.) B.J. Birch (ed.) , Computers in Number Theory, Proc. Sci. Research Council Atlas Symp. no. 2 , Acad. Press (1971) pp. 49– 56 |
| [a12] | J. Lehner, "Cohomology of vector-valued automorphic forms" Math. Ann. , 204 (1973) pp. 155–176 |
| [a13] | J. Lehner, "The Eichler cohomology of a Kleinian group" Math. Ann. , 192 (1971) pp. 125–143 |
| [a14] | G. Shimura, "Sur les intégrales attachées aux formes automorphes" J. Math. Soc. Japan , 11 (1959) pp. 291–311 |
Eichler cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Eichler_cohomology&oldid=12564