Eichler cohomology
In [a2], M. Eichler conceived the "Eichler cohomology theory" (but not the designation) while studying "generalized Abelian integrals" (now called "Eichler integrals" ; see below).
The setting for this theory is that of automorphic forms, with multiplier system, on a discrete group $\Gamma$ of fractional-linear transformations (equivalently, of $( 2 \times 2 )$-matrices; cf. also Automorphic form; Fractional-linear mapping). One may assume that $\Gamma$ consists of real fractional-linear transformations, that is, that $\Gamma$ fixes $\mathcal{H}$, the upper half-plane. A fundamental region, $\mathcal{R}$, of $\Gamma$ is required to have finite hyperbolic area; this is equivalent to the two conditions (taken jointly):
i) $\Gamma$ is finitely generated;
ii) each real point $q$ of $\overline { \mathcal{R} }$ is a parabolic point (a cusp) of $\Gamma$, that is, it is fixed by a cyclic subgroup $\Gamma _ { q }$ of $\Gamma$ with parabolic generator.
Let $k \in \mathbf{Z}$ and let $\mathbf{v}$ be a multiplier system in weight $k$ with respect to $\Gamma$. Since $k$ is integral, this means simply that $|\mathbf{v} ( M ) | = 1$ for all $M \in \Gamma$, and $\mathbf{v}$ is multiplicative:
\begin{equation} \tag{a1} \mathbf{v} ( M _ { 1 } , M _ { 2 } ) = \mathbf{v} ( M _ { 1 } ) \mathbf{v} ( M _ { 2 } ) , M _ { 1 } , M _ { 2 } \in \Gamma. \end{equation}
For $M \in \Gamma$ and $\varphi$ a function on $\mathcal{H}$, define the slash operator
\begin{equation} \tag{a2} ( \varphi | _ { k } ^ { \mathbf{v} } M ) ( z ) = {\bf v} ( M ) ( cz + d ) ^ { - k } \varphi ( M z ). \end{equation}
In this notation, the characteristic transformation law satisfied by an automorphic form $f$ on $\Gamma$ of weight $k$ and multiplier system $\mathbf{v}$ can be written
\begin{equation} \tag{a3} f | _ { k } ^ { \mathbf{v} } M = f , \forall M \in \Gamma. \end{equation}
Let $\{ \Gamma , k , \mathbf{v} \}$ denote the vector space of automorphic forms on $\Gamma$ of weight $k$ and multiplier system $\mathbf{v}$, the collection of $f$ satisfying (a3) and that are holomorphic on $\mathcal{H}$ and meromorphic at each parabolic cusp of $\overline { \mathcal{R} }$ (in the usual local variable, cf. also Analytic function; Meromorphic function). One says that $f \in \{ \Gamma , k , \mathbf{v} \}$ is an entire automorphic form if $f$ is holomorphic at each parabolic cusp. An entire automorphic form $f$ is called a cusp form if $f$ vanishes at each parabolic cusp. As usual, $C ^ { + } ( \Gamma , k , \mathbf{v} )$ denotes the space of entire automorphic forms and $C ^ { 0 } ( \Gamma , k , \mathbf{v} )$ denotes the subspace of cusp forms. For groups $\Gamma$ of the kind considered here, a suitable version of the Riemann–Roch theorem shows that $C ^ { + } ( \Gamma , k , \mathbf{v} )$ has finite dimension over $\mathbf{C}$.
To describe the genesis of Eichler cohomology it is helpful to introduce the Bol identity [a1]:
\begin{equation} \tag{a4} D ^ { k + 1 } \{ ( c z + d ) ^ { k } F ( M z ) \} = \end{equation}
\begin{equation*} = ( c z + d ) ^ { - k - 2 } F ^ { ( k + 1 ) } ( M z ), \end{equation*}
where $k \in \mathbf{Z}$, 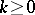 , $M = \left( \begin{array} { c c } { * } & { * } \\ { c } & { d } \end{array} \right)$ is any fractional-linear transformation of determinant $1$, and $F$ is a function with $k + 1$ derivatives ((a4) is easily derived from the Cauchy integral formula, cf. Cauchy integral theorem, or proved by induction on $k$). As a consequence of (a4), if $F \in \{ \Gamma , - k , \mathbf{v} \}$, then $F ^ { ( k + 1 ) } \in \{ \Gamma , k + 2 , \mathbf{v} \}$.
, $M = \left( \begin{array} { c c } { * } & { * } \\ { c } & { d } \end{array} \right)$ is any fractional-linear transformation of determinant $1$, and $F$ is a function with $k + 1$ derivatives ((a4) is easily derived from the Cauchy integral formula, cf. Cauchy integral theorem, or proved by induction on $k$). As a consequence of (a4), if $F \in \{ \Gamma , - k , \mathbf{v} \}$, then $F ^ { ( k + 1 ) } \in \{ \Gamma , k + 2 , \mathbf{v} \}$.
There is a second consequence of (a4), more directly relevant to the case under consideration: if $f \in \{ \Gamma , k + 2 , \mathbf{v} \}$ and $F ^ { ( k + 1 ) } = f$ (for example, $F ( z ) = ( 1 / k ! ) \int _ { i } ^ { z } f ( \tau ) ( z - \tau ) ^ { k } d \tau$), then $F$ satisfies
\begin{equation} \tag{a5} F | _ { - k } ^ { \mathbf{v} } M = F + p _ { M } , \forall M \in \Gamma, \end{equation}
where $p_{M}$ is a polynomial in $z$ of degree at most $k$. $F$ is called an Eichler integral of weight $- { k }$ and multiplier system $\mathbf{v}$, with respect to $\Gamma$, and with period polynomials $p_{M}$, $M \in \Gamma$. Eichler integrals generalize the classical Abelian integrals (cf. Abelian integral), which occur as the case $k = 0$, $\mathbf{v} \equiv 1$. As an immediate consequence of (a5), $\{ p _ { M } : M \in \Gamma \}$ satisfies the cocycle condition
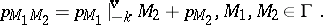 | (a6) |
Consider the cocycle condition for $\{ p _ { M } : M \in \Gamma \}$ in the space $P ( k )$ of polynomials of degree at most $k$. A collection of polynomials $\{ p _ { M } \in P ( k ) : M \in \Gamma \}$ satisfying (a6) is called a cocycle in $P ( k )$. A coboundary in $P ( k )$ is a collection $\{ p _ { M } \in P ( k ) : M \in \Gamma \}$ such that
\begin{equation} \tag{a7} p _ { M } = p | _ { - k } ^ { \mathbf{v} } M - p , M \in \Gamma , \end{equation}
with a fixed polynomial $p \in P ( k )$. Note that $\{ p _ M\}$ defined by (a7) satisfies (a6). The Eichler cohomology group $H ^ { 1 } = H ^ { 1 } ( \Gamma , k , \mathbf{v} ; P ( k ) )$ is now defined to be the quotient space: cocycles in $P ( k )$ modulo coboundaries in $P ( k )$.
To state Eichler's cohomology theorem of [a2] one must introduce the notion of a "parabolic cocycle" . Let $q _ { 1 } , \dots , q _ { t }$ be the (necessarily finite) set of inequivalent parabolic cusps in $\overline { \mathcal{R} }$. For $1 \leq h \leq t$, let $\Gamma _ { h }$ be the stabilizer of $q_h$ in $\Gamma$ with parabolic generator $Q _ { h }$ (cf. also Stabilizer). One says that the cocycle $\{ p _ { M } \in P ( k ) : M \in \Gamma \}$ is parabolic if the following holds: For each $h$, $1 \leq h \leq t$, there exists a $p _ { h } \in P ( k )$ such that 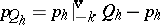 .
.
Coboundaries are of course parabolic cocycles, so one may form the quotient group: parabolic cocycles in $P ( k )$ modulo coboundaries in $P ( k )$. This is a subgroup of $H ^ { 1 } ( \Gamma , k , \mathbf{v} ; P ( k ) )$, called the parabolic Eichler cohomology group and denoted by $\tilde { H } ^ { 1 } = \tilde { H } ^ { 1 } ( \Gamma , k , {\bf v} ; P ( k ) )$.
Eichler's theorem [a2], p. 283, states: The vector spaces $C ^ { 0 } ( \Gamma , k + 2 , \overline{\mathbf{v}} ) \oplus C ^ { 0 } ( \Gamma , k + 2 , \mathbf{v} )$ and $\widetilde { H } ^ { 1 } ( \Gamma , k , \mathbf v ; P ( k ) )$ are isomorphic under a canonical mapping.
The discussion above, leading to (a6), shows how to associate a unique element $\beta ( f )$ of $\widetilde { H } ^ { 1 }$ to $f \in C ^ { 0 } ( \Gamma , k + 2 , \mathbf{v} )$, by forming a $( k + 1 )$-fold anti-derivative of $f$. The key to the proof of Eichler's theorem lies in the construction of a suitable mapping $\alpha ( g )$ from $g \in C ^ { 0 } ( \Gamma , k + 2 , \mathbf{v} )$ to $\widetilde { H } ^ { 1 }$. Eichler accomplishes this by attaching to $g$ an element $\hat{g}$ of $\{ \Gamma , k + 2 , \mathbf{v} \}$ with poles in $\overline { \mathcal{R} }$, and then passing to the cocycle of period polynomials of a $( k + 1 )$-fold anti-derivative of $\hat{g}$. The mapping $\mu$ from $C ^ { 0 } ( \Gamma , k + 2 , \overline{\mathbf{v}} ) \oplus C ^ { 0 } ( \Gamma , k + 2 , \mathbf{v} )$ to $\widetilde { H } ^ { 1 }$ is then defined by means of $\mu ( g , f ) = \alpha ( g ) + \beta ( f )$. The proof that $\mu$ is one-to-one follows from Eichler's generalization of the Riemann period relation for Abelian integrals to the setting of Eichler integrals.
The proof can be completed by showing that $\operatorname { dim } \tilde { H } ^ { 1 } = \operatorname { dim } C ^ { 0 } ( \Gamma , k + 2 , \overline{\mathbf{v}} ) + \operatorname { dim } C ^ { 0 } ( \Gamma , k + 2 ,\mathbf{v} )$. The essence of Eichler's theorem is that every parabolic cocycle can be realized as the system of period polynomials of some unique Eichler integral of weight $- { k }$ and multiplier system $\mathbf{v}$, with respect to $\Gamma$.
R.C. Gunning [a3] has proved a related result, from which Eichler's theorem follows as a corollary: The vector spaces $C ^ { 0 } ( \Gamma , k + 2 , \overline{\mathbf{v}} ) \oplus C ^ { + } ( \Gamma , k + 2 , \mathbf{v} )$ and $H ^ { 1 } ( \Gamma , k , \mathbf{v} ; P ( k ) )$ are isomorphic under the mapping of Eichler's theorem.
Proving Gunning 's theorem first and then deriving Eichler's theorem from it has the advantage that the calculation of $\operatorname{dim} \, H ^ { 1 }$ is substantially easier than that of $\operatorname{dim} \tilde { H } _ { 1 }$; this, because in $H ^ { 1 }$ there is no restriction on the elements of $P ( k )$ associated to the parabolic generators $Q _ { h }$, $1 \leq h \leq t - 1$.
There are various proofs of Gunning 's theorem and its corollary, in addition to those in [a2], [a3]. See, for example, [a4], [a11], [a14]. (G. Shimura [a14] has refined Eichler's theorem by working over the real rather than the complex field.) In [a6], Chap. 5, [a7], [a8], and [a13], analogous results are proved for the more general situation in which $\Gamma$ is a finitely generated Kleinian group. I. Kra has made further contributions to this case ([a9], [a10]).
The literature contains several results describing the cohomology groups $H ^ { 1 }$ and $\widetilde { H } ^ { 1 }$ that arise when the space of polynomials $P ( k )$ is replaced by a larger space of analytic functions [a3], Thm. 3, [a5], Thms. 1; 2, [a7], Thm. 5. Gunning [a3], Thms. 4; 5, discusses $H ^ { 0 }$ and $H ^ { p }$, for $p > 1$, as well as $H ^ { 1 }$. For an overview see [a5].
References
| [a1] | G. Bol, "Invarianten linearer Differentialgleichungen" Abh. Math. Sem. Univ. Hamburg , 16 : 3–4 (1949) pp. 1–28 |
| [a2] | M. Eichler, "Eine Verallgemeinerung der Abelschen Integrale" Math. Z. , 67 (1957) pp. 267–298 |
| [a3] | R.C. Gunning, "The Eichler cohomology groups and automorphic forms" Trans. Amer. Math. Soc. , 100 (1961) pp. 44–62 |
| [a4] | S.Y. Hussemi, M.I. Knopp, "Eichler cohomology and automorphic forms" Illinois J. Math. , 15 (1971) pp. 565–577 |
| [a5] | M.I. Knopp, "Some new results on the Eichler cohomology of automorphic forms" Bull. Amer. Math. Soc. , 80 (1974) pp. 607–632 |
| [a6] | I. Kra, "Automorphic forms and Kleinian groups" , Benjamin (1972) |
| [a7] | I. Kra, "On cohomology of Kleinian groups" Ann. of Math. , 89 : 2 (1969) pp. 533–556 |
| [a8] | I. Kra, "On cohomology of Kleinian groups - II" Ann. of Math. , 90 : 2 (1969) pp. 576–590 |
| [a9] | I. Kra, "On cohomology of Kleinian groups - III" Acta Math. , 127 (1971) pp. 23–40 |
| [a10] | I. Kra, "On cohomology of Kleinian groups - IV" J. d'Anal. Math. , 43 (1983-84) pp. 51–87 |
| [a11] | J. Lehner, "Automorphic Integrals with preassigned period polynomials and the Eichler cohomology" A.O.L. Atkin (ed.) B.J. Birch (ed.) , Computers in Number Theory, Proc. Sci. Research Council Atlas Symp. no. 2 , Acad. Press (1971) pp. 49– 56 |
| [a12] | J. Lehner, "Cohomology of vector-valued automorphic forms" Math. Ann. , 204 (1973) pp. 155–176 |
| [a13] | J. Lehner, "The Eichler cohomology of a Kleinian group" Math. Ann. , 192 (1971) pp. 125–143 |
| [a14] | G. Shimura, "Sur les intégrales attachées aux formes automorphes" J. Math. Soc. Japan , 11 (1959) pp. 291–311 |
Eichler cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Eichler_cohomology&oldid=12564