Ehresmann connection
The genesis of the general concept of connection on an arbitrary fibred manifold 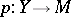 ,
, 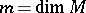 , was inspired by a paper by Ch. Ehresmann, [a1], where he analyzed the classical approaches to connections from the global point of view (cf. also Connections on a manifold; Fibre space; Manifold). The main idea is that at each point
, was inspired by a paper by Ch. Ehresmann, [a1], where he analyzed the classical approaches to connections from the global point of view (cf. also Connections on a manifold; Fibre space; Manifold). The main idea is that at each point 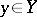 one prescribes an
one prescribes an 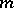 -dimensional linear subspace
-dimensional linear subspace 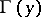 of the tangent space
of the tangent space 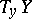 of
of 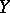 which is complementary to the tangent space
which is complementary to the tangent space 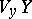 of the fibre passing through
of the fibre passing through 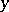 . These spaces are called the horizontal spaces of
. These spaces are called the horizontal spaces of 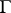 . Hence
. Hence 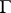 is an
is an 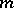 -dimensional distribution on
-dimensional distribution on 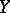 .
.
There are three main ways to interpret an Ehresmann connection 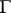 :
:
1) As the lifting mapping 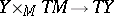 , transforming every vector
, transforming every vector 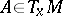 into the unique vector
into the unique vector 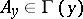 satisfying
satisfying 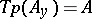 ,
, 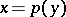 . So, every vector field
. So, every vector field 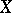 on
on 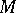 is lifted into a vector field
is lifted into a vector field 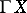 on
on 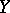 . The parallel transport on
. The parallel transport on 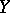 along a curve
along a curve 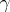 on
on 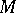 is determined by the integral curves of the lifts of the tangent vectors of
is determined by the integral curves of the lifts of the tangent vectors of 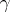 .
.
2) As the connection form 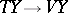 , transforming every vector of
, transforming every vector of 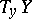 into its first component with respect to the direct sum decomposition
into its first component with respect to the direct sum decomposition 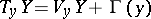 . Since the vertical tangent bundle
. Since the vertical tangent bundle 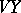 is a subbundle of
is a subbundle of 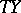 , the connection form is a special tangent-valued one-form on
, the connection form is a special tangent-valued one-form on 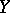 .
.
3) 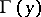 is identified with an element of the first jet prolongation
is identified with an element of the first jet prolongation 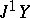 of
of 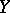 . Then
. Then 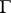 is interpreted as a section
is interpreted as a section 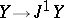 .
.
If  is a vector bundle and
is a vector bundle and 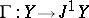 is a linear morphism, then
is a linear morphism, then 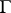 is called a linear connection. (From this viewpoint, an Ehresmannn connection is also said to be a non-linear connection.) A classical connection on a manifold
is called a linear connection. (From this viewpoint, an Ehresmannn connection is also said to be a non-linear connection.) A classical connection on a manifold  corresponds to a linear connection on the tangent bundle
corresponds to a linear connection on the tangent bundle 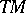 . If
. If 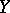 is a principal fibre bundle with structure group
is a principal fibre bundle with structure group 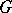 , and
, and 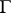 is
is 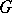 -invariant, then
-invariant, then 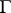 is called a principal connection. These connections have been used most frequently. On the other hand, a big advantage of connections without any additional structure is that prolongation procedures of functorial character can be applied to them with no restriction.
is called a principal connection. These connections have been used most frequently. On the other hand, a big advantage of connections without any additional structure is that prolongation procedures of functorial character can be applied to them with no restriction.
The main geometric object determined by 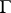 is its curvature. This is a section
is its curvature. This is a section 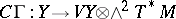 , whose definition varies according to the above three cases.
, whose definition varies according to the above three cases.
1) This is the obstruction 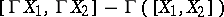 for lifting the bracket of vector fields
for lifting the bracket of vector fields 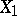 ,
, 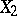 on
on 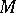 .
.
2) 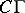 is one half of the Frölicher–Nijenhuis bracket
is one half of the Frölicher–Nijenhuis bracket 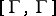 of the tangent-valued one-form
of the tangent-valued one-form 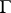 with itself.
with itself.
3) Consider the jet prolongation 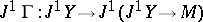 . Then
. Then 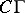 characterizes the deviation of
characterizes the deviation of 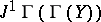 from the second jet prolongation
from the second jet prolongation 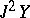 of
of 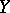 , which is a subspace of
, which is a subspace of 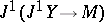 .
.
The curvature of 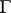 vanishes if and only if the distribution
vanishes if and only if the distribution 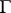 is a foliation.
is a foliation.
Every Ehresmann connection satisfies the Bianchi identity. In the second approach, this is the relation
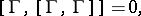 |
which is one of the basic properties of the Frölicher–Nijenhuis bracket. For a classical connection on 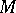 , this relation coincides with the second Bianchi identity.
, this relation coincides with the second Bianchi identity.
For every section 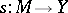 , one defines its absolute differential
, one defines its absolute differential 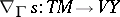 as the projection of the tangent mapping
as the projection of the tangent mapping 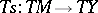 in the direction of the horizontal spaces. Iterated absolute differentiation is based on the fact that every Ehresmann connection on
in the direction of the horizontal spaces. Iterated absolute differentiation is based on the fact that every Ehresmann connection on 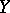 induces canonically an Ehresmann connection on
induces canonically an Ehresmann connection on 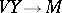 , [a2].
, [a2].
If a tangent-valued one-form 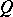 on
on 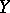 is given, then the Frölicher–Nijenhuis bracket
is given, then the Frölicher–Nijenhuis bracket 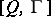 is called the
is called the 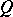 -torsion of
-torsion of  . This leads to a far-reaching generalization of the concept of torsion of a classical connection, [a3]. Even in this case, the basic properties of the Frölicher–Nijenhuis bracket yield a relation
. This leads to a far-reaching generalization of the concept of torsion of a classical connection, [a3]. Even in this case, the basic properties of the Frölicher–Nijenhuis bracket yield a relation
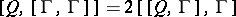 |
which generalizes the first Bianchi identity of a classical connection.
A systematic presentation of the theory of Ehresmann connections (under the name of general connections) can be found in [a2].
References
| [a1] | C. Ehresmann, "Les connections infinitésimales dans un espace fibré différentiable" Colloq. de Topol., CBRM, Bruxelles (1950) pp. 29–55 |
| [a2] | I. Kolář, P.W. Michor, J. Slovák, "Natural operations in differential geometry" , Springer (1993) |
| [a3] | Modugno, M., "Torsion and Ricci tensor for non-linear connections" Diff. Geom. Appl. , 1 (1991) pp. 177–192 |
Ehresmann connection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ehresmann_connection&oldid=18987