Egorov generalized function algebra

Given an open subset of , Yu.V. Egorov [a1] defined the generalized function algebra as the factor algebra of modulo the ideal of sequences which vanish eventually on every compact subset of . The family provides a sheaf of differential algebras on . Convolution with a sequence of mollifiers , where 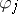converges to the Dirac measure, gives an imbedding of the space 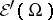of compactly supported distributions into 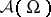which respects derivatives as well as supports. It can be extended as a sheaf morphism to an imbedding of the space of distributions .

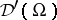As a generalized function algebra, can be employed to study non-linear partial differential equations. In particular, Egorov has used the algebra to construct generalized solutions to boundary value problems as well as evolution equations. In the latter case the spatial derivative 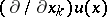may be replaced by the difference operator

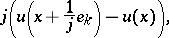where 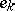denotes the 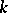th unit vector in 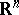. This way partial differential equations are approximated by ordinary difference-differential equations in the algebra .

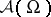See also Generalized function algebras.

References

[a1]	Yu.V. Egorov, "A contribution to the theory of generalized functions" Russian Math. Surveys , 45 : 5 (1990) pp. 1–49