Eckmann-Hilton duality
A duality principle variously described as "...a metamathematical principle that corresponding to a theorem there is a dual theorem (each of these dual theorems being proved separately)" [a4], "...a guiding principle to the homotopical foundations of algebraic topology..." [a1], "...a principle or yoga rather than a theorem" [a5], and "...a commonplace of experience among topologists, accepted as obvious" [a3]. The duality provides a categorical point of view for clarifying and unifying various aspects of pointed homotopy theory, but is often heuristic rather than strictly categorical.
Any notion (definition, theorem, etc.) in a category 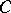 which can be expressed purely category-theoretically admits a formal dual in the opposite or dual category
which can be expressed purely category-theoretically admits a formal dual in the opposite or dual category  , which can then be re-interpreted as a notion in the original category
, which can then be re-interpreted as a notion in the original category 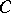 ; this latter notion is the (Eckmann–Hilton) dual of the original notion. As examples, the notions of monomorphism in
; this latter notion is the (Eckmann–Hilton) dual of the original notion. As examples, the notions of monomorphism in 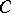 and epimorphism in
and epimorphism in 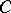 are dual, as are the notions of product of objects in
are dual, as are the notions of product of objects in 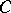 and co-product of objects in
and co-product of objects in 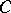 . Pursuing the second example, an object
. Pursuing the second example, an object 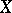 in
in  (assumed to have zero-mappings) is group-like if there is a morphism
(assumed to have zero-mappings) is group-like if there is a morphism 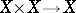 in
in 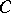 ,
, 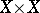 denoting the product of
denoting the product of 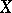 with itself, satisfying the group axioms, expressed arrow-theoretically; dually,
with itself, satisfying the group axioms, expressed arrow-theoretically; dually, 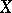 in
in 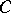 is co-group-like if there is a morphism
is co-group-like if there is a morphism  in
in 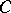 ,
, 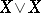 denoting the co-product of
denoting the co-product of 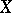 with itself, satisfying the group axioms with arrows reversed. If
with itself, satisfying the group axioms with arrows reversed. If 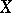 is group-like (respectively, co-group-like), the morphism set
is group-like (respectively, co-group-like), the morphism set 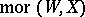 (respectively,
(respectively, 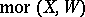 ) inherits a natural group structure.
) inherits a natural group structure.
In the category 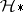 of pointed CW-complexes (cf. also CW-complex; Pointed space) and pointed homotopy classes of mappings, "product" is Cartesian product and "co-product" is one-point union. The most familiar group-like (respectively, co-group-like) objects are loop spaces (respectively, suspensions) (cf. also Suspension; Loop space). If the requirements of associativity and existence of inverses are dropped from the group axioms, the resulting objects are
of pointed CW-complexes (cf. also CW-complex; Pointed space) and pointed homotopy classes of mappings, "product" is Cartesian product and "co-product" is one-point union. The most familiar group-like (respectively, co-group-like) objects are loop spaces (respectively, suspensions) (cf. also Suspension; Loop space). If the requirements of associativity and existence of inverses are dropped from the group axioms, the resulting objects are 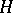 -spaces (respectively, co-
-spaces (respectively, co-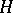 -spaces; cf. also
-spaces; cf. also 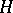 -space; Co-
-space; Co-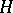 -space). An important generalization of co-
-space). An important generalization of co-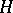 -spaces is obtained by considering the notion of Lyusternik–Shnirel'man category (cf. also Category (in the sense of Lyusternik–Shnirel'man)). Originally conceived as a geometric invariant of a space
-spaces is obtained by considering the notion of Lyusternik–Shnirel'man category (cf. also Category (in the sense of Lyusternik–Shnirel'man)). Originally conceived as a geometric invariant of a space  (
(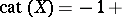 the minimum cardinality of an open covering of
the minimum cardinality of an open covering of 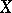 , each of whose members is contractible in
, each of whose members is contractible in  ), the definition can be recast (G.W. Whitehead, T. Ganea) in ways that are susceptible to dualization (see [a3] for a useful bibliography, including references to sources for
), the definition can be recast (G.W. Whitehead, T. Ganea) in ways that are susceptible to dualization (see [a3] for a useful bibliography, including references to sources for 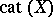 and various candidates for a dual,
and various candidates for a dual, 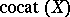 ).
).  is a co-
is a co-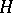 -space if and only if
-space if and only if  .
.
At the beginning of their work on duality in 1955, B. Eckmann and P. Hilton studied the category 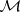 of modules (over some ring) and developed two dual notions of module homotopy (cf. also Homotopy): injective homotopy, where, for a module
of modules (over some ring) and developed two dual notions of module homotopy (cf. also Homotopy): injective homotopy, where, for a module 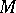 , an injective module containing
, an injective module containing 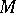 plays the role of the "cone" over
plays the role of the "cone" over 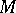 ; and projective homotopy, where a projective module mapping onto
; and projective homotopy, where a projective module mapping onto  plays the role of the "path space" over
plays the role of the "path space" over 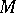 . These two versions of homotopy in
. These two versions of homotopy in 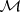 are different but their analogues in
are different but their analogues in 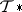 , the category of pointed CW-complexes and pointed mappings, are identical owing to the adjunction equivalence
, the category of pointed CW-complexes and pointed mappings, are identical owing to the adjunction equivalence
 |
applied with  ; here
; here 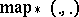 is the morphism set in
is the morphism set in 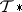 , suitably topologized,
, suitably topologized, 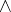 is smash product and
is smash product and 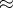 is homeomorphism [a1]. In other words, the duality between projective and injective modules in
is homeomorphism [a1]. In other words, the duality between projective and injective modules in 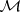 becomes an internal duality in the topological context.
becomes an internal duality in the topological context.
The adjunction equivalence  , with
, with 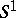 the circle, induces an adjunction equivalence
the circle, induces an adjunction equivalence
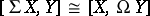 |
in 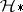 ; here
; here 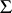 ,
,  and
and 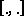 denote suspension, loop space and morphism set in
denote suspension, loop space and morphism set in 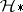 . Using iterated suspensions and loop spaces, one introduces
. Using iterated suspensions and loop spaces, one introduces
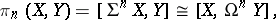 |
simultaneously generalizing the cohomology groups of 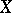 (when
(when 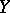 is an Eilenberg–MacLane space) and the homotopy groups of
is an Eilenberg–MacLane space) and the homotopy groups of  (when
(when 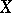 is the
is the  -sphere and
-sphere and 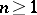 ). (When
). (When 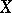 is a Moore space of type
is a Moore space of type  , with
, with 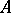 an Abelian group, one obtains homotopy groups with coefficients.) The
an Abelian group, one obtains homotopy groups with coefficients.) The 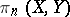 may be generalized to
may be generalized to 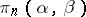 , where
, where 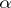 ,
, 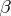 are mappings; namely,
are mappings; namely, 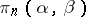 is set equal to the homotopy classes of commutative diagrams
is set equal to the homotopy classes of commutative diagrams 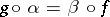 . Various relative groups are special cases of this general construction and the standard exact sequences of algebraic topology ensue, in dual pairs. Also, the Postnikov decomposition of a path-connected space
. Various relative groups are special cases of this general construction and the standard exact sequences of algebraic topology ensue, in dual pairs. Also, the Postnikov decomposition of a path-connected space 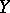 (where the basic building blocks are Eilenberg–MacLane spaces) and the Moore decomposition of a
(where the basic building blocks are Eilenberg–MacLane spaces) and the Moore decomposition of a 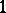 -connected space
-connected space 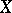 (where the basic building blocks are Moore spaces) are dual to one another; these two decompositions appear as special cases of what Eckmann and Hilton describe as the homotopy decomposition, respectively the homology decomposition of a map
(where the basic building blocks are Moore spaces) are dual to one another; these two decompositions appear as special cases of what Eckmann and Hilton describe as the homotopy decomposition, respectively the homology decomposition of a map 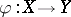 .
.
Again appealing to the adjunction equivalence in 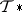 , one observes that the topological notion of fibration (homotopy lifting property) dualizes to the notion of cofibration (homotopy extension property). Similarly, HELP (homotopy extension and lifting property) dualizes to co–HELP; [a1], Thms. 4; 4
, one observes that the topological notion of fibration (homotopy lifting property) dualizes to the notion of cofibration (homotopy extension property). Similarly, HELP (homotopy extension and lifting property) dualizes to co–HELP; [a1], Thms. 4; 4 . But HELP leads to the theorem of J.H.C. Whitehead that a mapping of path-connected CW-complexes inducing isomorphisms on homotopy groups is a homotopy equivalence [a1], Thm. A, while co–HELP leads to another Whitehead theorem that a mapping of path-connected nilpotent CW-complexes inducing isomorphisms on homology groups is a homotopy equivalence [a1], Thm. B. Thus, the two illustrious Whitehead theorems are Eckmann–Hilton dual, with dual proofs. (Cf. also Homotopy group.)
. But HELP leads to the theorem of J.H.C. Whitehead that a mapping of path-connected CW-complexes inducing isomorphisms on homotopy groups is a homotopy equivalence [a1], Thm. A, while co–HELP leads to another Whitehead theorem that a mapping of path-connected nilpotent CW-complexes inducing isomorphisms on homology groups is a homotopy equivalence [a1], Thm. B. Thus, the two illustrious Whitehead theorems are Eckmann–Hilton dual, with dual proofs. (Cf. also Homotopy group.)
It is not true, however, that dual theorems necessarily admit dual proofs. An example is afforded by theorems of I.M. James and T. Ganea characterizing path-connected 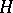 -spaces and path-connected co-
-spaces and path-connected co-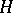 -spaces, respectively. Thus, the path-connected space
-spaces, respectively. Thus, the path-connected space 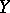 is an
is an 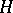 -space if and only if the canonical mapping
-space if and only if the canonical mapping  , adjoint to the identity mapping of
, adjoint to the identity mapping of  , admits a left homotopy inverse and the path-connected space
, admits a left homotopy inverse and the path-connected space 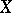 is a co-
is a co- -space if and only if the canonical mapping
-space if and only if the canonical mapping 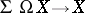 , adjoint to the identity mapping of
, adjoint to the identity mapping of 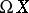 , admits a right homotopy inverse. No known proof of either theorem dualizes to a proof of the other.
, admits a right homotopy inverse. No known proof of either theorem dualizes to a proof of the other.
It is also possible that the dual of a theorem is false. As an example, consider the well-known result that the suspension of the loop space of a sphere is homotopy equivalent to a co-product of spheres. The dual would assert that the loop space of the suspension of an Eilenberg–MacLane space is homotopy equivalent to a product of Eilenberg–MacLane spaces. However, this assertion fails already in the case that the Eilenberg–MacLane space is the circle 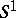 .
.
Sometimes the strict dual of a result turns out to admit a surprisingly interesting variant. A theorem of Hilton [a2], Ref. H82, asserts that co-product cancellation fails for finite CW-complexes; there exist 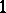 -connected
-connected  -cell CW-complexes
-cell CW-complexes 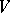 ,
,  and a sphere
and a sphere 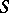 such that
such that 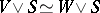 but
but 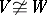 . This theorem dualizes straightforwardly to an example of the failure of product cancellation; there exist
. This theorem dualizes straightforwardly to an example of the failure of product cancellation; there exist 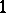 -connected, 2-stage Postnikov systems
-connected, 2-stage Postnikov systems 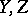 and an Eilenberg–MacLane space
and an Eilenberg–MacLane space  such that
such that 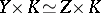 but
but 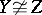 . The much more delicate question of failure of product cancellation for
. The much more delicate question of failure of product cancellation for 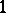 -connected, finite CW-complexes was studied by P. Hilton and J. Roitberg [a2], Ref. H98. One of their examples leads to the existence of a finite CW-complex which is an
-connected, finite CW-complexes was studied by P. Hilton and J. Roitberg [a2], Ref. H98. One of their examples leads to the existence of a finite CW-complex which is an 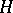 -space (indeed, a loop space) not homotopy equivalent to any of the "classical"
-space (indeed, a loop space) not homotopy equivalent to any of the "classical"  -spaces. This example, along with other examples of A. Zabrodsky [a6] helped usher in a new subdiscipline of homotopy theory, that of "finite H-spaces" and "finite loop spaces" .
-spaces. This example, along with other examples of A. Zabrodsky [a6] helped usher in a new subdiscipline of homotopy theory, that of "finite H-spaces" and "finite loop spaces" .
A conscientious Eckmann–Hilton dualist might enquire about the existence of duals of finite 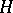 -spaces; these would be finite Postnikov spaces which are co-
-spaces; these would be finite Postnikov spaces which are co-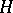 -spaces. Since a non-contractible,
-spaces. Since a non-contractible,  -connected, finite Postnikov space cannot be a co-
-connected, finite Postnikov space cannot be a co-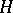 -space (the Lyusternik–Shnirel'man category of such a space is infinite according to Y. Félix, S. Halperin, J.-M. Lemaire and J.-C. Thomas [a7]), it follows that
-space (the Lyusternik–Shnirel'man category of such a space is infinite according to Y. Félix, S. Halperin, J.-M. Lemaire and J.-C. Thomas [a7]), it follows that  , the co-product of finitely many circles, is the only path-connected finite Postnikov space admitting a co-
, the co-product of finitely many circles, is the only path-connected finite Postnikov space admitting a co-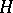 -space structure. Thus the dual of a spicy piece of homotopy theory can be rather bland.
-space structure. Thus the dual of a spicy piece of homotopy theory can be rather bland.
The space 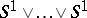 calls to mind another example, discussed in [a2], and given here. If
calls to mind another example, discussed in [a2], and given here. If 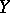 is a path-connected
is a path-connected 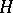 -space of finite homotopical type (all homotopy groups are finitely generated), then there exists an
-space of finite homotopical type (all homotopy groups are finitely generated), then there exists an 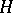 -space
-space 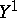 with
with 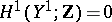 and a homotopy equivalence from
and a homotopy equivalence from  to
to 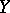 . Dually, if
. Dually, if 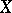 is a path-connected co-
is a path-connected co-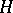 -space of finite homological type (all homology groups are finitely generated), there exists a
-space of finite homological type (all homology groups are finitely generated), there exists a 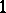 -connected co-
-connected co-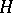 -space
-space 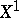 and a mapping from
and a mapping from 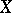 to
to  inducing homology isomorphisms. In 1971, Ganea posed the question of whether
inducing homology isomorphisms. In 1971, Ganea posed the question of whether 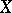 is homotopy equivalent to such a co-product. Recently (1997), N. Iwase has announced a negative answer to this question.
is homotopy equivalent to such a co-product. Recently (1997), N. Iwase has announced a negative answer to this question.
References
| [a1] | J.P. May, "The dual Whitehead theorems" I.M. James (ed.) , Topological Topics. Articles on Algebra and Topology presented to Prof. P.J. Hilton in celebration of his sixtieth birthday , London Math. Soc. Lecture Notes , 86 , Cambridge Univ. Press (1983) pp. 46–54 |
| [a2] | G. Mislin, "Essay on Hilton's work in topology" I.M. James (ed.) , Topological Topics. Articles on Algebra and Topology presented to Prof. P.J. Hilton in celebration of his sixtieth birthday , London Math. Soc. Lecture Notes , 86 , Cambridge Univ. Press (1983) pp. 15–30 |
| [a3] | P. Hilton, "Duality in homotopy theory: a restrospective essay" J. Pure Appl. Algebra , 19 (1980) pp. 159–169 |
| [a4] | E.H. Spanier, "Review of: B. Eckmann, Homotopie et dualité, Colloque de topologie algebrique, Louvain 1956, Masson, 1957, 41–53" Math. Reviews , 19 (1958) pp. 570c |
| [a5] | J. Stasheff, "Hilton–Eckmann duality revisited" Contemp. Math. , 37 (1985) pp. 149–152 |
| [a6] | A. Zabrodsky, "Homotopy associativity and finite CW-complexes" Topology , 9 (1970) pp. 121–128 |
| [a7] | Y. Felix, S. Halperin, J.-M. Lemaire, J.-C. Thomas, "Mod 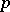 loop space homology" Invent. Math. , 95 (1989) pp. 247–262 loop space homology" Invent. Math. , 95 (1989) pp. 247–262 |
Eckmann-Hilton duality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Eckmann-Hilton_duality&oldid=22369