E-M-factorization-system-in-a-category
The simple fact that every function 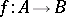 between sets can be factored through its image (i.e., written as a composite
between sets can be factored through its image (i.e., written as a composite
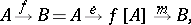 |
where 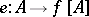 is the codomain-restriction of
is the codomain-restriction of 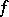 and
and 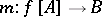 is the inclusion) is abstracted in category theory to an axiomatic theory of factorization structures
is the inclusion) is abstracted in category theory to an axiomatic theory of factorization structures 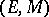 for morphisms of a category
for morphisms of a category 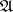 . Here,
. Here, 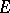 and
and 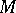 are classes of
are classes of 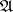 -morphisms (the requirements
-morphisms (the requirements 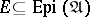 and
and 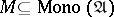 were originally included, but later dropped) such that each
were originally included, but later dropped) such that each 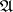 -morphism has an
-morphism has an 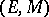 -factorization
-factorization
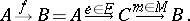 |
Clearly, further assumptions on 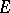 and
and 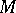 are required to make the factorization theory useful. A careful analysis has revealed that the crucial requirement that causes
are required to make the factorization theory useful. A careful analysis has revealed that the crucial requirement that causes 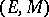 -factorizations to have appropriate characteristics is the so-called "unique E,M-diagonalization" condition, described in 3) below. Such factorization structures for morphisms have turned out to be especially useful for "well-behaved" categories (e.g., those having products and satisfying suitable smallness conditions). Morphism factorizations have been transformed into powerful categorical tools by successive generalizations to
-factorizations to have appropriate characteristics is the so-called "unique E,M-diagonalization" condition, described in 3) below. Such factorization structures for morphisms have turned out to be especially useful for "well-behaved" categories (e.g., those having products and satisfying suitable smallness conditions). Morphism factorizations have been transformed into powerful categorical tools by successive generalizations to
a) factorization structures for sources in a category;
b) factorization structures for structured sources with respect to a functor;
c) factorization structures for flows in a category; and
d) factorization structures for structured flows with respect to a functor. The simplest of these is described first and in most detail. A general reference for this area is [a1], Chaps. IV; V.
Let 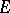 and
and 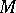 be classes of morphisms in a category
be classes of morphisms in a category 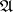 (cf. also Morphism). Then
(cf. also Morphism). Then 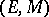 is called a factorization structure for morphisms in
is called a factorization structure for morphisms in 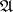 , and
, and 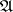 is called
is called 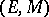 -structured, provided that
-structured, provided that
1) each of 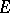 and
and 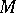 is closed under composition with isomorphisms;
is closed under composition with isomorphisms;
2) 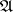 has
has 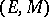 -factorizations (of morphisms); i.e., each morphism
-factorizations (of morphisms); i.e., each morphism 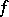 in
in  has a factorization
has a factorization 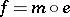 , with
, with 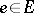 and
and 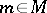 ; and
; and
3) 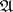 has the unique
has the unique 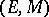 -diagonalization property; i.e., for each commutative square
-diagonalization property; i.e., for each commutative square
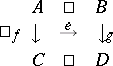 |
with 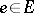 and
and 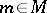 , there exists a unique diagonal, i.e., a morphism
, there exists a unique diagonal, i.e., a morphism 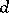 such that
such that 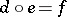 and
and 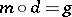 . For example, the category
. For example, the category  of sets and functions has exactly four different factorization structures for morphisms, the most frequently used of which is
of sets and functions has exactly four different factorization structures for morphisms, the most frequently used of which is 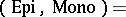 (surjections, injections) described above, whereas the category
(surjections, injections) described above, whereas the category 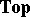 of topological spaces and continuous functions has more than a proper class of different factorization structures for morphisms (see [a6]), but
of topological spaces and continuous functions has more than a proper class of different factorization structures for morphisms (see [a6]), but 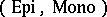 is not one of them (since it does not satisfy the diagonalization condition).
is not one of them (since it does not satisfy the diagonalization condition).
Diagonalization is crucial in that it guarantees essential uniqueness of factorizations. Also, it can be shown that each of 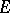 and
and 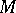 determines the other via the diagonal property, that
determines the other via the diagonal property, that 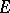 and
and 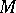 are compositive, and that
are compositive, and that 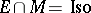 . Many other pleasant properties of
. Many other pleasant properties of 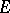 and
and 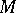 follow from the definition above.
follow from the definition above. 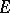 and
and 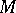 are dual to each other,
are dual to each other, 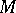 is well-behaved with respect to limits and
is well-behaved with respect to limits and 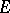 is well-behaved with respect to co-limits. Also, there exist satisfactory external characterizations of classes
is well-behaved with respect to co-limits. Also, there exist satisfactory external characterizations of classes 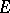 in a category that guarantee the existence of a class
in a category that guarantee the existence of a class 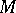 such that
such that 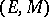 will be a factorization system for morphisms (see, e.g., [a2]). Many familiar categories have particular morphism factorization structures. Every finitely-complete category that has intersections is
will be a factorization system for morphisms (see, e.g., [a2]). Many familiar categories have particular morphism factorization structures. Every finitely-complete category that has intersections is 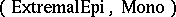 -structured. Each category that has equalizers and intersections is
-structured. Each category that has equalizers and intersections is 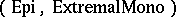 -structured, and a category that has pullbacks and co-equalizers is
-structured, and a category that has pullbacks and co-equalizers is 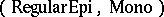 -structured if and only if regular epimorphisms in it are compositive.
-structured if and only if regular epimorphisms in it are compositive.
Factorization structures for sources (i.e., families of morphisms with a common domain) in a category 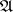 are defined quite analogously to those for single morphisms. Here, one has a class
are defined quite analogously to those for single morphisms. Here, one has a class 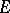 of morphisms and a family
of morphisms and a family 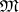 of sources, each closed under composition with isomorphisms, such that each source
of sources, each closed under composition with isomorphisms, such that each source 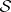 in
in 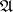 has a factorization
has a factorization 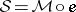 with
with 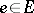 and
and 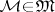 , and each commuting square in
, and each commuting square in 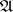 , with sources as right side and bottom side, a member of
, with sources as right side and bottom side, a member of 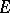 as top side and a member of
as top side and a member of 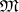 as bottom side, has a diagonalization. A category that has these properties is called an
as bottom side, has a diagonalization. A category that has these properties is called an 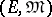 -category. Notice that now
-category. Notice that now 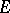 and
and 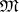 are no longer dual. The dual theory is that of a factorization structure for sinks, i.e., an
are no longer dual. The dual theory is that of a factorization structure for sinks, i.e., an 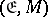 -category. Interestingly, in any
-category. Interestingly, in any 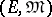 -category,
-category, 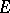 must be contained in the class of all epimorphisms. (As a consequence, uniqueness of the diagonal comes without hypothesizing it.) However,
must be contained in the class of all epimorphisms. (As a consequence, uniqueness of the diagonal comes without hypothesizing it.) However, 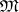 is contained in the family of all mono-sources if and only if
is contained in the family of all mono-sources if and only if 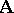 has co-equalizers and
has co-equalizers and 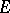 contains all regular epimorphisms. There exist reasonable external characterizations of classes
contains all regular epimorphisms. There exist reasonable external characterizations of classes 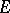 in a category that guarantee the existence of a family
in a category that guarantee the existence of a family 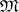 such that
such that 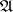 is an
is an 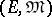 -category (see e.g., [a1], 15.14) and a reasonable theory exists for extending factorization structures for morphisms to those for sources (respectively, sinks).
-category (see e.g., [a1], 15.14) and a reasonable theory exists for extending factorization structures for morphisms to those for sources (respectively, sinks).
Factorization structures with respect to functors provide yet a further generalization, as follows.
Let 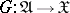 be a functor, let
be a functor, let 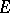 be a class of
be a class of 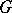 -structured arrows, and let
-structured arrows, and let 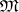 be a conglomerate of
be a conglomerate of 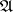 -sources.
-sources. 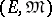 is called a factorization structure for
is called a factorization structure for 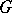 , and
, and 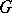 is called an
is called an 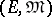 -functor provided that:
-functor provided that:
A) 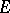 and
and 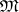 are closed under composition with isomorphisms;
are closed under composition with isomorphisms;
B) 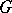 has
has 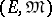 -factorizations, i.e., for each
-factorizations, i.e., for each 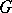 -structured source
-structured source 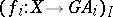 there exist
there exist
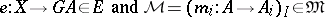 |
such that
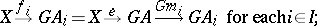 |
C) 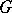 has the unique
has the unique 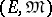 -diagonalization property, i.e., whenever
-diagonalization property, i.e., whenever 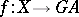 and
and 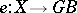 are
are 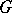 -structured arrows with
-structured arrows with 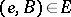 , and
, and 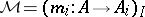 and
and 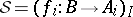 are
are 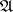 -sources with
-sources with 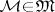 , such that
, such that 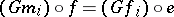 for each
for each 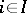 , then there exists a unique diagonal, i.e., an
, then there exists a unique diagonal, i.e., an 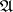 -morphism
-morphism 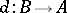 with
with 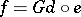 and
and 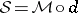 .
.
Interestingly, this precisely captures the important categorical notion of adjointness: i.e., a functor is an adjoint functor if and only if it is an 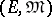 -functor for some
-functor for some 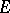 and
and 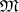 .
.
Generalizations of factorization theory to flows and flows with respect to a functor can be found in [a5] and [a11], respectively.
References
| [a1] | J. Adamek, H. Herrlich, G.E. Strecker, "Abstract and concrete categories" , Wiley–Interscience (1990) |
| [a2] | A.K. Bousfield, "Constructions of factorization systems in categories" J. Pure Appl. Algebra , 9 (1977) pp. 207–220 |
| [a3] | C. Cassidy, M. Hébert, G.M. Kelly, "Reflective subcategories, localizations and factorization systems" J. Austral. Math. Soc. , 38 (1985) pp. 287–329 (Corrigenda: 41 (1986), 286) |
| [a4] | P.J. Freyd, G.M. Kelly, "Categories of continuous functors I" J. Pure Appl. Algebra , 2 (1972) pp. 169–191 |
| [a5] | H. Herrlich, W. Meyer, "Factorization of flows and completeness of categories" Quaest. Math. , 17 : 1 (1994) pp. 1–11 |
| [a6] | H. Herrlich, G. Salicrup, R. Vazquez, "Dispersed factorization structures" Canad. J. Math. , 31 (1979) pp. 1059–1071 |
| [a7] | H. Herrlich, G.E. Strecker, "Semi-universal maps and universal initial completions" Pacific J. Math. , 82 (1979) pp. 407–428 |
| [a8] | R.-E. Hoffmann, "Factorization of cones" Math. Nachr. , 87 (1979) pp. 221–238 |
| [a9] | R. Nakagawa, "A note on 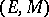 -functors" H. Herrlich (ed.) G. Preuss (ed.) , Categorical Topology , Lecture Notes Math. , 719 , Springer (1979) pp. 250–258 -functors" H. Herrlich (ed.) G. Preuss (ed.) , Categorical Topology , Lecture Notes Math. , 719 , Springer (1979) pp. 250–258 |
| [a10] | G.E. Strecker, "Perfect sources" A. Dold (ed.) B. Eckmann (ed.) , Categorical Topol. Proc. Conf. Mannheim 1975 , Lecture Notes Math. , 540 , Springer (1976) pp. 605–624 |
| [a11] | G.E. Strecker, "Flows with respect to a functor" Appl. Categorical Struct. (to appear) |
| [a12] | W. Tholen, "Factorizations of cones along a functor" Quaest. Math. , 2 (1977) pp. 335–353 |
| [a13] | W. Tholen, "Factorizations, localizations, and the orthogonal subcategory problem" Math. Nachr. , 114 (1983) pp. 63–85 |
E-M-factorization-system-in-a-category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=E-M-factorization-system-in-a-category&oldid=15835