Dynamics

A branch of mechanics which deals with the motion of material bodies taking place under the effect of forces acting upon them, which bring about motion or alter it — the so-called accelerating forces.

The foundations of dynamics were laid in the 17th century by G. Galileo, who was the first to study the motion of physical bodies under the effect of the force of gravity and established the law of inertia. The fundamental principles of dynamics were actually formulated by I. Newton in the form of three fundamental laws of mechanics and their consequences. Subsequent development and improvement of the laws of dynamics are due to L. Euler, J. d'Alembert and J.L. Lagrange, who gave general methods for establishing the equations of dynamics. The foundations of analytical methods for the study of the equations of dynamics were laid by Lagrange, W.R. Hamilton and C.G.J. Jacobi. Subsequent development of these methods formed the subject of studies by C.F. Gauss, M.V. Ostrogradski, H. Poincaré, S.A. Chaplygin, N.G. Chetaev, and others.

Dynamics based on the principles laid down by Galileo and by Newton is known as classical or Newtonian dynamics, as distinct from studies based on other principles (quantum dynamics, relativistic dynamics, etc.). Classical dynamics comprises the totality of mathematical derivations and conclusions which follow from the fundamental laws of Galileo and Newton. The axiomatic concepts include that of a fixed space (an absolute stationary (or inertial) reference system) and an absolute time which is the same for all points in space. It is assumed that the absolute space has all the properties of Euclidean space. Newton's laws are formulated with respect to the absolute space and absolute time. They remain valid in inertial reference systems. The conclusions as to the motion of material bodies are arrived at in dynamics by constructing models (of a material point, of a perfect solid, of a continuum, etc.).

As regards the nature of the problems studied, dynamics may be subdivided into dynamics of a material point and dynamics of a system of material points. The concept of a material point is a fundamental concept in classical dynamics. A material point is defined as a body whose geometrical dimensions can be neglected in the study of its motion, but whose mass is finite. Newton's first and second laws in dynamics are formulated for a material point only. Dynamics also considers the model of an absolute solid, the distances between the points of which remain unchanged during the motion. These basic models of dynamics yield solutions to a number of specific problems involving the motion of real bodies.

The dynamics of a system of material points concerns motions of bodies which are interconnected with each other. Dynamics of systems include dynamics of a solid, dynamics of a system with a variable mass, dynamics of elastic and plastically deformable bodies, dynamics of liquids and gases, etc.

The nature of the motion of a material system is determined by the forces acting upon the system (active forces) and by the constraints imposed on the points of the system, which can be replaced by forces of reaction (passive forces). The forces acting on a system of material points are the result of the interaction of individual material points, both those forming part of the system under study and those not forming part of it. Accordingly, one distinguishes between internal and external forces. The forces may be represented as a function of the positions and velocities of material points, and of time.

The two fundamental problems solved in dynamics are: 1) the determination of the force resulting in a specific motion of a material point or system; and 2) the determination of the motion of a material point or system taking place under the action of given forces. Problems in dynamics are solved with the aid of the differential equations of motion. In the case of a single material point these equations express Newton's second law, and may be written in the form:

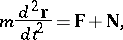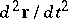where is the radius vector of the material point in the reference system studied, is its acceleration, 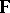is the active force acting on the point, and 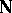is the force of reaction of the constraint. To determine the law of motion of the material point, the value of at any moment of time must be found. The integration of the equations of motions is realized with the aid of general theorems of dynamics (theorems on the change in the quantity of the motion, the moment of the quantity of the motion and the active forces). These theorems determine important physical relationships between the principal dynamic characteristics of motion and interaction between material bodies; in several cases the process of integration of the equations of dynamics is thus considerably simplified. Moreover, general theorems make it possible to study individual aspects of the motion under consideration. General theorems for a system of material points may be obtained by direct generalization of the general theorems applicable to a single material point. If the proof is based on the d'Alembert–Lagrange principle, the theorems become more satisfactory in that they do not involve the reaction of the constraint, but establish a direct connection between the dynamic magnitude describing the motion of the system and the active forces acting on the system. Systems with holonomic ideal constraints are the most widespread. The motion of such systems can be described by the Lagrange equations (in mechanics) of the second kind, which follow from the d'Alembert–Lagrange principle. These equations are most convenient for the study of the motion of systems of material points. For material systems with non-holonomic ideal constraints, the Appell equations give the most general description of the motion not involving the reactions of the constraints.

Analytical dynamics deals with the properties of the equations of motion of mechanical systems due to the specific form of such equations. Its field of study comprises the general principles of dynamics, the derivation of the differential equations of motion from these principles and methods for their integration. The methods of analytical dynamics are widely employed both in solving various problems in dynamics and in various other fields of physics. Of major importance in the study of the properties of the motion of mechanical systems are the canonical Hamilton equations, which aid in formulating several effective methods of solving problems in dynamics.

In addition to the general methods of formulation and integration of the equations of motion of material bodies acted upon by accelerating forces, dynamics also considers a number of special problems, including the dynamics of a solid body, the dynamics of gyroscopic systems, the theory of oscillations of mechanical systems, the theory of stability of motion, the theory of shocks, etc.

References

[1]	G. Galilei, "Unterredungen und mathematische Demonstration über zwei neue Wissenschaftszweige, die Mechanik und die Fallgesetze betreffend" , 1–2 , W. Engelmann , Leipzig (1891) (Translated from Italian and Greek)
[2]	G. Galileo, "Discours on the two most important world systems - Ptolemaic and Copernican" , Moscow-Leningrad (1948) (In Russian; translated from Italian)
[3]	I. Newton, "Mathematische Prinzipien der Naturlehre" , Springer (1872) (Translated from English)
[4]	L. Euler, "Principles of point dynamics" , Moscow-Leningrad (1938) (In Russian; translated from Latin)
[5]	J. d'Alembert, "Abhandlung über die Dynamik" , Ostwald Klassiker , 106 (Translated from French)
[6]	J.L. Lagrange, "Mécanique analytique" , 1–2 , Paris (1788) ((Also: Oeuvres, Vol. 11.))
[7]	C.G.J. Jacobi, "Vorlesungen über Dynamik" , G. Reimer (1884)
[8]	W. Hamilton, "On a general method in dynamics..." , Variational principles of mechanics , Moscow (1959) (In Russian; translated from English)
[9]	H. Hertz, "Prinzipien der Mechanik" , Gesammelte Werke , 3 , Barth , Leipzig (1894)
[10]	M.V. Ostrogradskii, "Lectures on analytical mechanics" , Complete works , 2 , Kiev (1961) (In Russian)
[11]	N.E. Zhukovskii, "Theoretical mechanics" , Moscow-Leningrad (1952) (In Russian)
[12]	S.A. Chaplygin, "A course of lectures on theoretical dynamics" , Collected works , 4 , Moscow-Leningrad (1949) (In Russian)
[13]	N.G. Chetaev, "Stability of motion" , Moscow (1962) (In Russian)

Comments

The constraints present in a dynamical system can be of various types. Consider (for the sake of being definite) a collection of 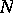particles moving in -space. Then the following three types of constrained equations are considered:

i) the vanishing of certain functions of the 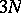Cartesian position coordinates;

ii) inequalities of certain functions of these coordinates;

iii) (linear) non-integrable relations between the differentials of these coordinates.

Constraints of the first type are called holonomic; those of types ii), iii) non-holonomic. The word "ideal" in "ideal holonomic constraintideal holonomic constraints" refers to idealized properties of the constraints. E.g., if the constraints can be thought of as a string linking two particles, this string is of weight zero and perfectly inextensible, and if a material point is constrained to stay on one side of a surface this surface is perfectly rigid.

References

[a1]	E.T. Whittaker, "Analytical dynamics of particles and rigid bodies" , Dover, reprint (1944)
[a2]	V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian)
[a3]	E.C.G. Sudarshan, N. Mukunda, "Classical dynamics: a modern perspective" , Wiley (Interscience) (1974)