Dynamic problems of elasticity theory
A type of problems in elasticity theory concerning the propagation of vibrations or states of stationary vibration in elastic media. In the simplest case, which is also the most important one in practical applications — the linear theory of homogeneous isotropic elastic bodies — such problems may be reduced to seeking the solution of the Lamé equation:
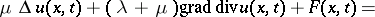 | (1) |
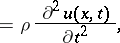 |
which satisfies, in a given range, the specified initial and boundary conditions. Here  is the displacement vector at the point
is the displacement vector at the point 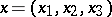 at time
at time 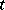 , the
, the  are volume forces,
are volume forces, 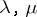 are the Lamé constants, and
are the Lamé constants, and  is the density.
is the density.
By virtue of being an equation of hyperbolic type, equation (1) permits a real characteristic surface 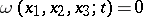 along which the derivatives of the solution, which are usually of an order higher than one, lose their continuity (weak discontinuity). The discontinuity surface is propagated in space at the rate
along which the derivatives of the solution, which are usually of an order higher than one, lose their continuity (weak discontinuity). The discontinuity surface is propagated in space at the rate
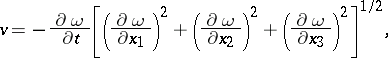 |
thus separating two solutions at any moment of time. The equation of this surface is obtained from the fact that it is impossible to determine uniquely all the derivatives at its points if the first derivatives are known, using equation (1). It follows from the equation of the discontinuity surface:
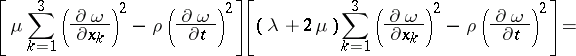 |
 |
that there exist two rates of displacement of this surface:
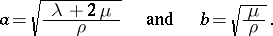 |
These rates are the rates of displacement of two types of deformation in a linear elastic isotropic body:  is the rate of propagation of longitudinal perturbations, while
is the rate of propagation of longitudinal perturbations, while 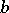 is the rate of propagation of lateral perturbations. It can also be shown that, in certain cases, surface waves may propagate along the interfaces, and that they have their own characteristic rates of propagation (Rayleigh waves on a free surface, Stoneley waves on the boundaries of elastic media).
is the rate of propagation of lateral perturbations. It can also be shown that, in certain cases, surface waves may propagate along the interfaces, and that they have their own characteristic rates of propagation (Rayleigh waves on a free surface, Stoneley waves on the boundaries of elastic media).
Cases in which discontinuities appear in the first derivatives of the displacement along the characteristics (strong discontinuity) have also been studied. If the jumps along the characteristic affect only the normal vector component 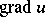 , while the tangential constituents of this vector and the displacements themselves remain continuous, the discontinuity is said to be a regular strong discontinuity. In such a case the conditions of kinematic and dynamic compatibility, which play an important role in solving dynamic problems by the method of characteristics, are satisfied on the characteristic surface.
, while the tangential constituents of this vector and the displacements themselves remain continuous, the discontinuity is said to be a regular strong discontinuity. In such a case the conditions of kinematic and dynamic compatibility, which play an important role in solving dynamic problems by the method of characteristics, are satisfied on the characteristic surface.
The effect of dynamic deformations of an elastic body becomes more complicated if this body has a finite boundary. Each point on such a boundary, as soon as it comes into contact with any one of the disturbances propagated from the fronts, which are themselves complicated, generates at least two new types of deformation.
Important special cases of equation (1) are those in which the field does not depend on time (statics), and in which it varies with time according to the law
 |
where 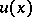 is a complex vector independent of time (the amplitude of the oscillations) and
is a complex vector independent of time (the amplitude of the oscillations) and 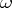 is the frequency of the established vibrations. In the latter case equation (1) is reduced to a system of equations which is elliptic with respect to the amplitude
is the frequency of the established vibrations. In the latter case equation (1) is reduced to a system of equations which is elliptic with respect to the amplitude
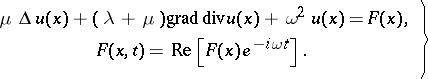 | (1prm) |
If the domain  in which the propagation of the vibrations is studied occupies the entire infinite space
in which the propagation of the vibrations is studied occupies the entire infinite space  , then the Cauchy problem with initial conditions
, then the Cauchy problem with initial conditions
 | (2) |
is well-posed for equation (1).
A fundamental role is played by special solutions of equation (1) which represent the displacement of an infinite elastic space under the effect of a force concentrated in a single point 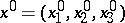 and having a magnitude equal to
and having a magnitude equal to 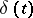 (where
(where 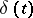 is the Dirac delta-function) (a fundamental solution).
is the Dirac delta-function) (a fundamental solution).
If the force is acting in the direction of the axis 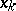 ,
, 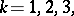 then the constituent displacements
then the constituent displacements 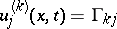 ,
, 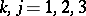 , have the following values:
, have the following values:
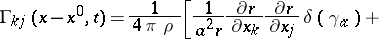 |
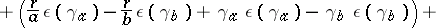 |
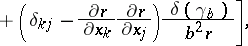 |
where
 |
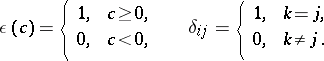 |
The matrix of fundamental solutions 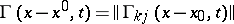 , of dimension
, of dimension 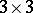 , represents a symmetric tensor; the solution of Cauchy's problem for equation (1) is expressed by Volterra's formula:
, represents a symmetric tensor; the solution of Cauchy's problem for equation (1) is expressed by Volterra's formula:
 | (3) |
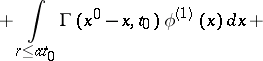 |
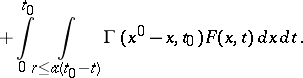 |
For the homogeneous system (1prm), 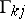 assumes the following form:
assumes the following form:
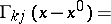 | (4) |
 |
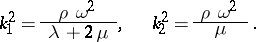 |
Not only Cauchy's problem, but also mixed problems may be formulated for equation (1). These are studied if the domain  has a boundary
has a boundary 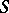 in a finite part of space. Boundary conditions on
in a finite part of space. Boundary conditions on 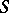 , which must be satisfied along with conditions (2), play an important role in this connection.
, which must be satisfied along with conditions (2), play an important role in this connection.
The following types of boundary problems are fundamental: first — the displacements are specified; secondly — the tensions are specified; thirdly — linear combinations of displacements and tensions are specified; fourthly — the normal component of the displacement and the tangential components of the tension are specified; fifthly — the tangential components of the displacement and the normal component of the tension are specified; and sixthly — the displacements are specified on one part of 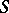 , while the tensions are specified on the complement.
, while the tensions are specified on the complement.
Unlike the Cauchy problem, which is completely solvable in general form by using formula (3), solutions of mixed problems have been obtained in special cases only. The most important ones are: solutions in closed form of the first and second fundamental mixed problems for a half-plane or a half-space, obtained by the method of complex waves and by a generalization of the method of characteristics; solutions of the wave equation for a sphere, obtained by the method of functional-invariant integrals; solutions of certain problems of elasticity theory by generalization of this method; and solutions of a number of diffraction problems. In the general case it is impossible to obtain solutions in closed forms; however, very general results may be obtained by methods of potential theory and the theory of singular integral equations.
Using the fundamental solutions (4), in analogy with the theory of harmonic potentials, it is possible to introduce the concepts of a single-layer, double-layer and a volume-mass elastic potential, which allow the regular solutions of equation (1prm) to be expressed by the formula
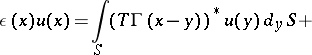 | (5) |
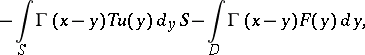 |
where 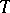 is the tension operator,
is the tension operator,  is the symbol of matrix transposition, and
is the symbol of matrix transposition, and 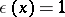 if
if 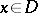 and
and 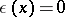 if
if 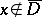 . The first five boundary conditions specified above make it possible to write down with the aid of potentials the respective problems in the form of two-dimensional singular integral equations on the closed surface
. The first five boundary conditions specified above make it possible to write down with the aid of potentials the respective problems in the form of two-dimensional singular integral equations on the closed surface 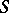 . It has been proved that all the problems are solvable for any oscillation frequency
. It has been proved that all the problems are solvable for any oscillation frequency 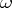 in the case of the exterior of a domain, and that there exists a discrete real non-negative spectrum of eigen frequencies for the interior problems. The solutions are expressed as Fourier series in a certain complete system of vectors, constructed with the aid of (4), and the Fourier coefficients are explicitly determined.
in the case of the exterior of a domain, and that there exists a discrete real non-negative spectrum of eigen frequencies for the interior problems. The solutions are expressed as Fourier series in a certain complete system of vectors, constructed with the aid of (4), and the Fourier coefficients are explicitly determined.
Let the displacement  on
on 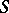 be given, let
be given, let 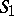 be an arbitrary smooth closed surface enclosing
be an arbitrary smooth closed surface enclosing 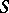 and having no points in common with it, and let
and having no points in common with it, and let 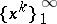 be a set of points on
be a set of points on 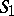 the distribution of which is everywhere dense. The columns of the matrix
the distribution of which is everywhere dense. The columns of the matrix 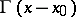 are denoted by
are denoted by 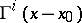 ,
, 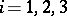 . It can be proved that the set of vectors
. It can be proved that the set of vectors 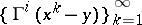 ,
,  ,
, 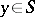 , is linearly independent and complete in
, is linearly independent and complete in 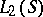 .
.
The elements in this set are numbered as follows:
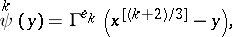 |
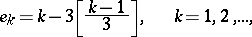 |
where 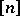 is the largest integer part of the number
is the largest integer part of the number  ; one also introduces the orthonormal set
; one also introduces the orthonormal set
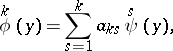 |
where 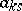 are given numbers. Then the solution of the problem at any interior point is expressed by the uniformly convergent series
are given numbers. Then the solution of the problem at any interior point is expressed by the uniformly convergent series
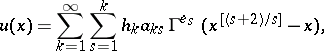 | (6) |
where
 |
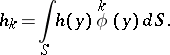 |
A finite initial partial sum of the series may be used to compute approximate values of the solution.
The results established for equation (1prm) make it possible to obtain solutions of mixed problems for equation (1) with the aid of the Laplace transform.
In studying the solutions of the Lamé equation for layered media one considers the propagation of individual waves or the interference of all generated waves. In the former approach, use is made of the finite rate of propagation of elastic waves, and the process of wave propagation inside the layers and the processes of reflection from and refraction by the boundaries are studied in succession. In constructing the interference solutions of the Lamé equation the boundary conditions at the boundary must be satisfied simultaneously, which results in an algebraic system of equations. In order to determine the proper processes in a layered system, the roots of the determinants of this system must be found; this operation can be reduced to the determination of the eigen values of certain operators. The eigen values (roots) may be both real and complex, depending on the nature of the operator. Real eigen values correspond to Rayleigh and Love interference waves which are propagated along the layer without exponential damping. The computation of the various characteristics of these waves under the conditions of a piecewise-continuous velocity is carried out on an electronic computer, and the results are used to construct theoretical seismograms.
Damped interference waves are connected with the complex eigen values of non-self-adjoint operators. Both types of interference waves are considered in seismics, in order to interpret the seismic waves observed in practical work.
In order to solve several problems on vibrations of homogeneous media, the method of functional-invariant solutions is used. In particular, study was made of the wave field generated by a point source in two elastic semi-spaces with a plane interface; the exact solutions yielded asymptotic formulas describing the wave field in near-frontal zones.
A geometric approximation, used both in stationary and in non-stationary variants, is of major importance in the theory of elastic waves. The displacement vector 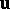 is found by using the series
is found by using the series
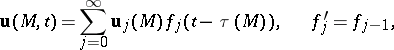 | (7) |
where the 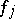 denote, in the non-stationary case, functions with a singular point at zero, while in the stationary case
denote, in the non-stationary case, functions with a singular point at zero, while in the stationary case
 |
Unlike in the scalar case, two kinds of series of the type (7) which formally satisfy the equations of the theory of elasticity are possible. These include the case of longitudinal waves, when
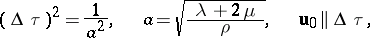 |
where  is the velocity of the longitudinal waves, and the case of transversal waves, when
is the velocity of the longitudinal waves, and the case of transversal waves, when
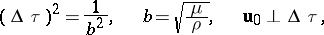 |
where 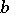 is the velocity of the transversal waves.
is the velocity of the transversal waves.
The vectors 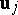 satisfy recurrence relations. Solutions of numerous problems of physical interest involve expansions of the type (7), and "waves" of this type may be reflected and refracted, as a result of which "waves" which can be represented by series of the type (7) are again obtained.
satisfy recurrence relations. Solutions of numerous problems of physical interest involve expansions of the type (7), and "waves" of this type may be reflected and refracted, as a result of which "waves" which can be represented by series of the type (7) are again obtained.
Methods of geometrical optics are also applicable in the case of surface waves. The boundary condition of zero tension on the surface may be satisfied by superposing longitudinal and transversal waves of the type (7) with complex eikonals. Such constructions yield a broad class of surface waves, of which the Rayleigh waves are a special instance.
It is also possible to develop a geometric-optical theory for surface waves of a different type: for waves a similar to Love waves, and for the so-called waves that are retained on the surface. The analogue of the Love waves in question are stationary high-frequency waves whose phase velocity is close to the velocity of transversal waves, while the direction of the displacement vector is, to a first approximation, the frequency of the normal to the surface and the direction of progagation of the wave. Waves that are retained by the surface also have a surface velocity close to that of the transversal waves, but their polarization is different — the displacement vector lies in the plane formed by the normal to the surface and the direction of propagation of the wave.
References
| [1] | F. Frank, R. von Mises, "Die Differential und Integralgleichungen der Mechanik und Physik" , 2 , Rosenberg (1943) pp. Chapt. 12 |
| [2] | K.I. Ogurtsov, G.I. Petrashen', Uchen. Zap. Leningrad. Gos. Univ. Ser. Mat. Nauk , 4 : 149 (1951) pp. 3–249 |
| [3] | V.M. Babich, M.P. [M.P. Kapilevich] Kapilewich, S.G. Mikhlin, "Lineare Differentialgleichungen der mathematischen Physik" , Akademie Verlag (1967) pp. Chapts. 1–2 (Translated from Russian) |
| [4] | O.A. Ladyzhenskaya, "A mixed problem for a hyperbolic equation" , Moscow (1953) (In Russian) |
| [5] | V.A. Il'in, "The solvability of mixed problems for hyperbolic and parabolic equations" Russian Math. Surveys , 15 : 2 (1960) pp. 85–142 Uspekhi Mat. Nauk , 15 : 2 (1960) pp. 97–154 |
| [6] | V.D. Kupradze, T.V. Burchuladze, T.G. Gegelia, M.O. Basheleishvili, "Three-dimensional problems of the mathematical theory of elasticity and thermoelasticity" , North-Holland (1979) (Translated from Russian) |
| [7] | G.I. Petrashen', "On a rational method of solving problems in the dynamical theory of elasticity in the case of isotropic layers with plane-parallel boundaries of separation" Uchen. Zap. Leningrad. Gos. Univ. , 30 : 208 (1956) pp. 5–57 (In Russian) |
| [8] | A.S. Alekseev, V.M. Babich, B.Ya. Gel'chinskii, "Problems in the dynamic theory of propagation of seismic waves" , 5 , Leningrad (1961) pp. 3–24 (In Russian) |
| [9] | V.M. Babich, "Propagation of Rayleigh waves along the surface of a homogeneous elastic body of arbitrary shape" Dokl. Akad. Nauk SSSR , 137 : 6 (1961) pp. 1263–1266 (In Russian) |
| [10] | V.M. Babich, I.A. Molotkov, Izv. Akad. Nauk SSSR. Fizika Zemli , 6 (1966) pp. 34–38 |
| [11] | I.V. Mukhina, I.A. Molotkov, Izv. Akad. Nauk SSSR. Fizika Zemli , 4 (1967) pp. 3–8 |
| [12a] | N.V. Svolinskii, Izv. Akad. Nauk SSSR. Ser. Geofiz. , 10 (1957) pp. 1201–1218 |
| [12b] | N.V. Svolinskii, Izv. Akad. Nauk SSSR. Ser. Geofiz. , 1 (1958) pp. 3–16 |
| [12c] | N.V. Svolinskii, Izv. Akad. Nauk SSSR. Ser. Geofiz. , 2 (1958) pp. 165–174 |
| [13] | Itogi Nauk. i Tekhn. Mekh. Tverd. Deform. Tel , 10 (1977) pp. 5–62 |
Comments
References
| [a1] | A.C. Eringen, E.S. Suhubi, "Elastodynamics" , 1–2 , Acad. Press (1974–1975) |
Dynamic problems of elasticity theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dynamic_problems_of_elasticity_theory&oldid=11485