Dupin indicatrix
curvature indicatrix
A plane curve illustrating the normal curvatures of a surface at a point of this surface. The Dupin indicatrix lies in the tangent plane to the surface  at the point
at the point  and there it is described by the radius vector
and there it is described by the radius vector  of length
of length  , where
, where  is the normal curvature of
is the normal curvature of  at
at  in the direction
in the direction  . Let
. Let  be a parametrization of
be a parametrization of 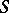 in a neighbourhood of
in a neighbourhood of 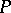 . One introduces a coordinate system on the tangent plane to
. One introduces a coordinate system on the tangent plane to  at
at 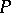 , taking
, taking 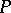 as the coordinate origin, and the vectors
as the coordinate origin, and the vectors 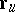 and
and 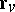 as the basis vectors of this coordinate system. The equation of the Dupin indicatrix will then be
as the basis vectors of this coordinate system. The equation of the Dupin indicatrix will then be
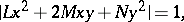 |
where  and
and 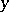 are the coordinates of a point on the Dupin indicatrix, and
are the coordinates of a point on the Dupin indicatrix, and  ,
, 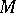 and
and 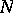 are the coefficients of the second fundamental form of
are the coefficients of the second fundamental form of 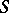 calculated at
calculated at  . The Dupin indicatrix is: a) an ellipse if
. The Dupin indicatrix is: a) an ellipse if 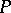 is an elliptic point (a circle if
is an elliptic point (a circle if 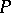 is an umbilical point); b) a pair of conjugate hyperbolas if
is an umbilical point); b) a pair of conjugate hyperbolas if 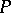 is a hyperbolic point; and c) a pair of parallel straight lines if
is a hyperbolic point; and c) a pair of parallel straight lines if 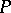 is a parabolic point. The curve is named after Ch. Dupin (1813), who was the first to use this curve in the study of surfaces.
is a parabolic point. The curve is named after Ch. Dupin (1813), who was the first to use this curve in the study of surfaces.

Figure: d034180a
References
| [1] | V.F. Kagan, "Foundations of the theory of surfaces in a tensor setting" , 2 , Moscow-Leningrad (1948) (In Russian) |
Comments
The Dupin indicatrix does not exist at a flat point.
The Dupin indicatrix at 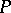 can be obtained as the limit of suitably normalized (inter)sections of the surface with planes parallel to the tangent plane of
can be obtained as the limit of suitably normalized (inter)sections of the surface with planes parallel to the tangent plane of 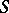 at
at  which are approaching this plane, see [a1], p. 370; [a2], p. 363-365.
which are approaching this plane, see [a1], p. 370; [a2], p. 363-365.
References
| [a1] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a2] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) |
| [a3] | C.C. Hsiung, "A first course in differential geometry" , Wiley (1981) pp. Chapt. 3, Sect. 4 |
Dupin indicatrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dupin_indicatrix&oldid=13694