Duncan-Mortensen-Zakai equation
DMZ equation
An equation whose solution is the unnormalized conditional probability density function for a non-linear filtering problem. The non-linear filtering problem was motivated by the solution of the linear filtering problem, especially in [a3], where the signal or state process is modeled by the solution of a linear differential equation with a Gaussian white noise input (the formal derivative of a Brownian motion or Wiener process), so the signal process is a Gauss–Markov process. The differential of the observation process, the process from which an estimate is made of the state process, is a linear transformation of the signal plus Gaussian white noise. This linear filtering problem was motivated by one where the infinite past of the observations [a5], [a7] is required. The non-linear filtering problem is described by a signal process that is the solution of a non-linear differential equation with a Gaussian white noise input and an observation process whose differential is a non-linear function of the signal process plus a Gaussian white noise. The precise description of such a filtering problem requires the theory of stochastic differential equations (e.g., [a4]; see also Stochastic differential equation).
Before introducing the Duncan–Mortensen–Zakai equation [a1], [a6], [a8], it is necessary to describe precisely a non-linear filtering problem. A basic filtering problem is described by two stochastic processes (cf. Stochastic process), 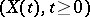 , which is called the signal or state process and
, which is called the signal or state process and 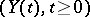 , which is called the observation process. These two processes satisfy the following stochastic differential equations:
, which is called the observation process. These two processes satisfy the following stochastic differential equations:
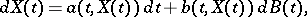 | (a1) |
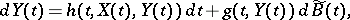 | (a2) |
where 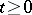 ,
, 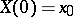 ,
, 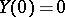 ,
, 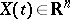 ,
,  ,
, 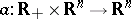 ,
, 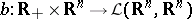 ,
, 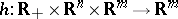 ,
,  , and
, and 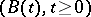 and
and 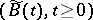 are independent standard Brownian motions in
are independent standard Brownian motions in  and
and 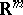 , respectively. The stochastic processes are defined on a fixed probability space
, respectively. The stochastic processes are defined on a fixed probability space 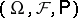 with a filtration
with a filtration 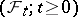 (cf. also Stochastic processes, filtering of). Some smoothness and non-degeneracy assumptions are made on the coefficients
(cf. also Stochastic processes, filtering of). Some smoothness and non-degeneracy assumptions are made on the coefficients  ,
, 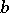 ,
, 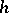 , and
, and 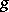 to ensure existence and uniqueness of the solutions of the stochastic differential equations (a1), (a2) and to ensure that the partial differential operators in the Duncan–Mortensen–Zakai equation are well defined.
to ensure existence and uniqueness of the solutions of the stochastic differential equations (a1), (a2) and to ensure that the partial differential operators in the Duncan–Mortensen–Zakai equation are well defined.
A filtering problem is to estimate 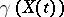 , where
, where 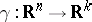 , based on the observations of (a2) until time
, based on the observations of (a2) until time 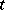 , that is,
, that is, 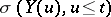 which is the sigma-algebra generated by the random variables
which is the sigma-algebra generated by the random variables 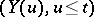 (cf. also Optional sigma-algebra).
(cf. also Optional sigma-algebra).
The conditional probability density of 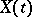 given
given 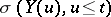 represents all of the probabilistic information of
represents all of the probabilistic information of 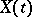 that is known from
that is known from  , that is, the observation process. A stochastic partial differential equation can be given for this conditional probability density function, but it satisfies a non-linear stochastic partial differential equation.
, that is, the observation process. A stochastic partial differential equation can be given for this conditional probability density function, but it satisfies a non-linear stochastic partial differential equation.
Let 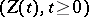 be the process that satisfies the stochastic differential equation
be the process that satisfies the stochastic differential equation
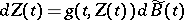 |
and 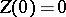 , which is obtained from (a2) by letting
, which is obtained from (a2) by letting 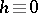 . The measures
. The measures 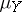 and
and 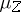 for the processes
for the processes 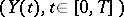 and
and 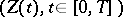 are mutually absolutely continuous (cf. also Absolute continuity) and
are mutually absolutely continuous (cf. also Absolute continuity) and
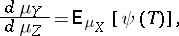 |
where
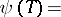 |
 |
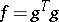 , and
, and 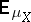 is integration on the measure for the process
is integration on the measure for the process 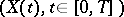 . Using some elementary properties of conditional mathematical expectation and absolute continuity of measures it follows that
. Using some elementary properties of conditional mathematical expectation and absolute continuity of measures it follows that
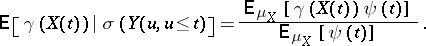 |
Thus, the unnormalized conditional probability density of 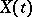 given
given 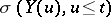 is
is
 |
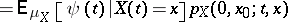 |
where 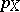 is the transition probability density (cf. also Transition probabilities) for the Markov process
is the transition probability density (cf. also Transition probabilities) for the Markov process  .
.
The function  satisfies a linear stochastic partial differential equation that is called the Duncan–Mortensen–Zakai equation [a1], [a6], [a8] and is given by
satisfies a linear stochastic partial differential equation that is called the Duncan–Mortensen–Zakai equation [a1], [a6], [a8] and is given by
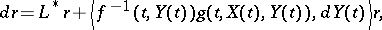 |
where  is the forward differential operator for the Markov process
is the forward differential operator for the Markov process 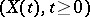 . The normalization factor for
. The normalization factor for  to obtain the conditional probability density is
to obtain the conditional probability density is 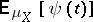 . An extensive description of the solution of a non-linear filtering problem can be found in [a2].
. An extensive description of the solution of a non-linear filtering problem can be found in [a2].
References
| [a1] | T.E. Duncan, "Probability densities for diffusion processes with applications to nonlinear filtering theory and detection theory" PhD Diss. Stanford Univ. (1967) |
| [a2] | G. Kallianpur, "Stochastic filtering theory" , Springer (1980) |
| [a3] | R.E. Kalman, R.S. Bucy, "New results in linear filtering and prediction" Trans. ASME Ser. D , 83 (1961) pp. 95–107 |
| [a4] | I. Karatzas, S.E. Shreve, "Brownian motion and stochastic calculus" , Springer (1991) (Edition: Second) |
| [a5] | A.N. Kolmogorov, "Sur l'interpolation et extrapolation des suites stationnaires" C.R. Acad. Sci. Paris , 208 (1939) pp. 2043 |
| [a6] | R.E. Mortensen, "Optimal control of continuous-time stochastic systems" PhD Diss. Univ. California, Berkeley (1966) |
| [a7] | N. Wiener, "Extrapolation, interpolation and smoothing of stationary time series with engineering applications" , Technol. Press&Wiley (1949) |
| [a8] | M. Zakai, "On the optimal filtering of diffusion processes" ZWvG , 11 (1969) pp. 230–243 |
Duncan-Mortensen-Zakai equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Duncan-Mortensen-Zakai_equation&oldid=14810