Duffin-Schaeffer conjecture

Let 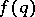be a function defined on the positive integers and let 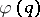be the Euler totient function. The Duffin–Schaeffer conjecture says that for an arbitrary function 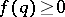(zero values are also allowed for 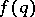), the Diophantine inequality (cf. also Diophantine equations)

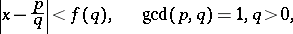(a1)

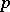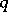has infinitely many integer solutions and for almost-all real (in the sense of Lebesgue measure) if and only if the series

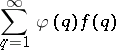(a2)

diverges. By the Borel–Cantelli lemma, (a1) has only finitely many solutions for almost-all if (a2) converges, and by the Gallagher ergodic theorem, the set of all for which (a1) has infinitely many integer solutions has measure either or .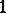

The Duffin–Schaeffer conjecture is one of the most important unsolved problems in the metric theory of numbers (as of 1998). It was inspired by an effort to replace 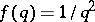by a smaller function 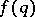for which every irrational number can be approximated by infinitely many fractions 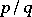such that (a1) holds. This question was answered by A. Hurwitz in 1891, who showed that the best possible function is 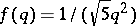. The application of Lebesgue measure to improve this 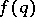was made by A. Khintchine [a7] in 1924. He proved that if 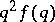is non-increasing and

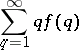(a3)

diverges, then (a1) has infinitely many integer solutions for almost-all . In 1941, R.J. Duffin and A.C. Schaeffer [a1] improved Khintchine's theorem for 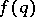satisfying 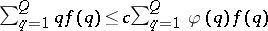for infinitely many 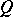and some positive constant . They also have given an example of an 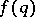such that (a3) diverges but (a2) converges which naturally leads to the Duffin–Schaeffer conjecture. Up to now (1998), this conjecture remains open. A breakthrough was achieved by P. Erdös [a2], who proved that the conjecture holds, given the additional condition 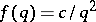or 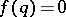for some 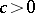. V.G. Sprindzuk comments in [a11] that the answer may depend upon the Riemann hypothesis (cf. also Riemann hypotheses). He also proposes the following 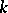-dimensional analogue of the Duffin–Schaeffer conjecture: There are infinitely many integers 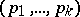and 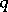such that

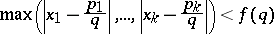and

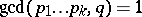for almost-all real numbers 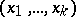whenever the series

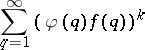(a4)

diverges. A.D. Pollington and R.C. Vaughan [a10] have proved this 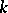-dimensional Duffin–Schaeffer conjecture for 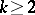. The corresponding result with 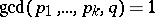instead of the condition 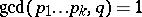was given by P.X. Gallagher [a3].

Various authors have studied the problem that the number of solutions of (a1) with 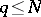is, for almost-all , asymptotically equal to .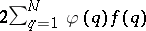

The problem of restricting both the numerators 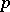and the denominators 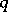in (a1) to sets of number-theoretic interest was investigated by G. Harman. In [a6] he considers (a1) where 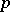, 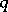are both prime numbers. In this case, the Duffin–Schaeffer conjecture has the form: If the sum

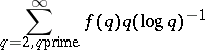(a5)

diverges, then for almost-all there are infinitely many prime numbers 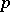, 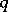which satisfy (a1). Harman has proved this conjecture under certain conditions on .

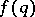A class of sequences 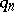, , 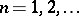of distinct positive integers and a class of functions 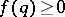is said to satisfy the Duffin–Schaeffer conjecture if the divergence of

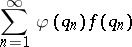(a6)

implies that for almost-all there exist infinitely many such that the Diophantine inequality

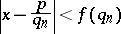has an integer solution 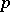that is mutually prime with 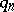(cf. also Mutually-prime numbers). There are tree types of results regarding 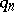, 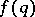satisfying this conjecture (cf. [a5]):

i) any one-to-one sequence 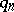and special 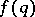(e.g. );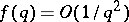

ii) any 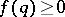and a special 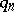(e.g. , );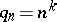

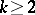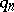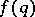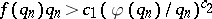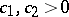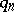iii) special , (e.g. for some ). As an interesting consequence of the Erdös result, for almost-all infinitely many denominators of the continued fraction convergents to lie in the sequence if and only if (a6) diverges.

Following J. Lesca [a8], one may extend the Duffin–Schaeffer conjecture to the problem of finding sequences 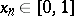such that for every non-increasing 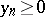, the divergence of

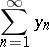(a7)

implies that for almost-all 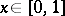there exist infinitely many such that 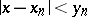. These 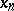are called eutaxic sequences. This problem encompasses all of the above conjectures.

As an illustration, let 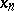be a sequence of reduced fractions with denominators 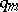, , 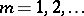and let 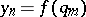for 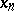with a fixed denominator 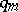. This gives the classical Duffin–Schaeffer conjecture, since (a6) and (a7) coincide. It is known that the sequence of fractional parts 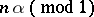is eutaxic if and only if the irrational number 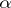has bounded partial quotients.

Finally, H. Nakada and G. Wagner [a9] have considered a complex version of the Duffin–Schaeffer conjecture for imaginary quadratic number fields.

The basic general reference books are [a11] and [a4].

References

[a1]	R.J. Duffin, A.C. Schaeffer, "Khintchine's problem in metric diophantine approximation" Duke Math. J. , 8 (1941) pp. 243–255
[a2]	P. Erdös, "On the distribution of convergents of almost all real numbers" J. Number Th. , 2 (1970) pp. 425–441
[a3]	P.X. Gallagher, "Metric simultaneous diophantine approximation II" Mathematika , 12 (1965) pp. 123–127
[a4]	G. Harman, "Metric number theory" , London Math. Soc. Monogr. , 18 , Clarendon Press (1998)
[a5]	G. Harman, "Some cases of the Duffin and Schaeffer conjecture" Quart. J. Math. Oxford , 41 : 2 (1990) pp. 395–404
[a6]	G. Harman, "Metric diophantine approximation with two restricted variables III. Two prime numbers" J. Number Th. , 29 (1988) pp. 364–375
[a7]	A. Khintchine, "Einige Saetze über Kettenbruche, mit Anwendungen auf die Theorie der Diophantischen Approximationen" Math. Ann. , 92 (1924) pp. 115–125
[a8]	J. Lesca, "Sur les approximations diophantiennes a'une dimension" Doctoral Thesis Univ. Grenoble (1968)
[a9]	H. Nakada, G. Wagner, "Duffin–Schaeffer theorem of diophantine approximation for complex number" Astérisque , 198–200 (1991) pp. 259–263
[a10]	A.D. Pollington, R.C. Vaughan, "The 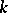-dimensional Duffin and Schaeffer conjecture" Mathematika , 37 : 2 (1990) pp. 190–200
[a11]	V.G. Sprindzuk, "Metric theory of diophantine approximations" , Winston&Wiley (1979)