Difference between revisions of "Duffin-Schaeffer conjecture"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Duffin–Schaeffer conjecture to Duffin-Schaeffer conjecture: ascii title) |
(No difference)
| |
Revision as of 18:51, 24 March 2012
Let 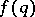 be a function defined on the positive integers and let
be a function defined on the positive integers and let 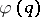 be the Euler totient function. The Duffin–Schaeffer conjecture says that for an arbitrary function
be the Euler totient function. The Duffin–Schaeffer conjecture says that for an arbitrary function 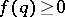 (zero values are also allowed for
(zero values are also allowed for 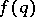 ), the Diophantine inequality (cf. also Diophantine equations)
), the Diophantine inequality (cf. also Diophantine equations)
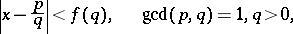 | (a1) |
has infinitely many integer solutions 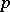 and
and 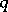 for almost-all real
for almost-all real  (in the sense of Lebesgue measure) if and only if the series
(in the sense of Lebesgue measure) if and only if the series
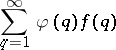 | (a2) |
diverges. By the Borel–Cantelli lemma, (a1) has only finitely many solutions for almost-all  if (a2) converges, and by the Gallagher ergodic theorem, the set of all
if (a2) converges, and by the Gallagher ergodic theorem, the set of all  for which (a1) has infinitely many integer solutions has measure either
for which (a1) has infinitely many integer solutions has measure either  or
or 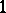 .
.
The Duffin–Schaeffer conjecture is one of the most important unsolved problems in the metric theory of numbers (as of 1998). It was inspired by an effort to replace 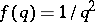 by a smaller function
by a smaller function 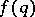 for which every irrational number
for which every irrational number  can be approximated by infinitely many fractions
can be approximated by infinitely many fractions 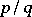 such that (a1) holds. This question was answered by A. Hurwitz in 1891, who showed that the best possible function is
such that (a1) holds. This question was answered by A. Hurwitz in 1891, who showed that the best possible function is 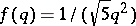 . The application of Lebesgue measure to improve this
. The application of Lebesgue measure to improve this 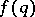 was made by A. Khintchine [a7] in 1924. He proved that if
was made by A. Khintchine [a7] in 1924. He proved that if 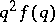 is non-increasing and
is non-increasing and
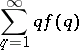 | (a3) |
diverges, then (a1) has infinitely many integer solutions for almost-all  . In 1941, R.J. Duffin and A.C. Schaeffer [a1] improved Khintchine's theorem for
. In 1941, R.J. Duffin and A.C. Schaeffer [a1] improved Khintchine's theorem for 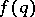 satisfying
satisfying 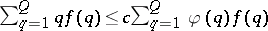 for infinitely many
for infinitely many 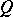 and some positive constant
and some positive constant  . They also have given an example of an
. They also have given an example of an 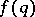 such that (a3) diverges but (a2) converges which naturally leads to the Duffin–Schaeffer conjecture. Up to now (1998), this conjecture remains open. A breakthrough was achieved by P. Erdös [a2], who proved that the conjecture holds, given the additional condition
such that (a3) diverges but (a2) converges which naturally leads to the Duffin–Schaeffer conjecture. Up to now (1998), this conjecture remains open. A breakthrough was achieved by P. Erdös [a2], who proved that the conjecture holds, given the additional condition 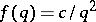 or
or 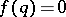 for some
for some 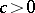 . V.G. Sprindzuk comments in [a11] that the answer may depend upon the Riemann hypothesis (cf. also Riemann hypotheses). He also proposes the following
. V.G. Sprindzuk comments in [a11] that the answer may depend upon the Riemann hypothesis (cf. also Riemann hypotheses). He also proposes the following 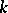 -dimensional analogue of the Duffin–Schaeffer conjecture: There are infinitely many integers
-dimensional analogue of the Duffin–Schaeffer conjecture: There are infinitely many integers 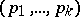 and
and 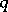 such that
such that
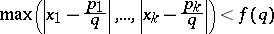 |
and
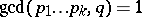 |
for almost-all real numbers 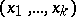 whenever the series
whenever the series
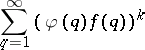 | (a4) |
diverges. A.D. Pollington and R.C. Vaughan [a10] have proved this 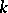 -dimensional Duffin–Schaeffer conjecture for
-dimensional Duffin–Schaeffer conjecture for 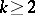 . The corresponding result with
. The corresponding result with 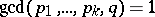 instead of the condition
instead of the condition 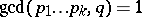 was given by P.X. Gallagher [a3].
was given by P.X. Gallagher [a3].
Various authors have studied the problem that the number of solutions of (a1) with 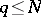 is, for almost-all
is, for almost-all  , asymptotically equal to
, asymptotically equal to 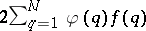 .
.
The problem of restricting both the numerators 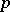 and the denominators
and the denominators 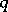 in (a1) to sets of number-theoretic interest was investigated by G. Harman. In [a6] he considers (a1) where
in (a1) to sets of number-theoretic interest was investigated by G. Harman. In [a6] he considers (a1) where 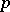 ,
, 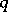 are both prime numbers. In this case, the Duffin–Schaeffer conjecture has the form: If the sum
are both prime numbers. In this case, the Duffin–Schaeffer conjecture has the form: If the sum
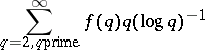 | (a5) |
diverges, then for almost-all  there are infinitely many prime numbers
there are infinitely many prime numbers 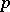 ,
, 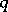 which satisfy (a1). Harman has proved this conjecture under certain conditions on
which satisfy (a1). Harman has proved this conjecture under certain conditions on 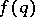 .
.
A class of sequences 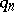 ,
, 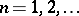 , of distinct positive integers and a class of functions
, of distinct positive integers and a class of functions 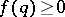 is said to satisfy the Duffin–Schaeffer conjecture if the divergence of
is said to satisfy the Duffin–Schaeffer conjecture if the divergence of
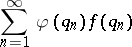 | (a6) |
implies that for almost-all  there exist infinitely many
there exist infinitely many  such that the Diophantine inequality
such that the Diophantine inequality
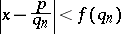 |
has an integer solution 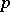 that is mutually prime with
that is mutually prime with 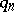 (cf. also Mutually-prime numbers). There are tree types of results regarding
(cf. also Mutually-prime numbers). There are tree types of results regarding 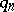 ,
, 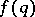 satisfying this conjecture (cf. [a5]):
satisfying this conjecture (cf. [a5]):
i) any one-to-one sequence 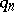 and special
and special 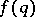 (e.g.
(e.g. 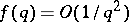 );
);
ii) any 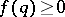 and a special
and a special 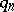 (e.g.
(e.g. 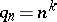 ,
, 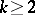 );
);
iii) special 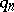 ,
, 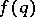 (e.g.
(e.g. 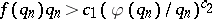 for some
for some 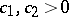 ). As an interesting consequence of the Erdös result, for almost-all
). As an interesting consequence of the Erdös result, for almost-all  infinitely many denominators of the continued fraction convergents to
infinitely many denominators of the continued fraction convergents to  lie in the sequence
lie in the sequence 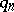 if and only if (a6) diverges.
if and only if (a6) diverges.
Following J. Lesca [a8], one may extend the Duffin–Schaeffer conjecture to the problem of finding sequences 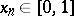 such that for every non-increasing
such that for every non-increasing 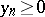 , the divergence of
, the divergence of
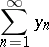 | (a7) |
implies that for almost-all 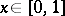 there exist infinitely many
there exist infinitely many  such that
such that 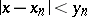 . These
. These 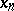 are called eutaxic sequences. This problem encompasses all of the above conjectures.
are called eutaxic sequences. This problem encompasses all of the above conjectures.
As an illustration, let 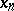 be a sequence of reduced fractions with denominators
be a sequence of reduced fractions with denominators 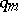 ,
, 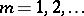 , and let
, and let 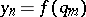 for
for 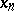 with a fixed denominator
with a fixed denominator 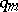 . This gives the classical Duffin–Schaeffer conjecture, since (a6) and (a7) coincide. It is known that the sequence of fractional parts
. This gives the classical Duffin–Schaeffer conjecture, since (a6) and (a7) coincide. It is known that the sequence of fractional parts 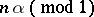 is eutaxic if and only if the irrational number
is eutaxic if and only if the irrational number 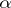 has bounded partial quotients.
has bounded partial quotients.
Finally, H. Nakada and G. Wagner [a9] have considered a complex version of the Duffin–Schaeffer conjecture for imaginary quadratic number fields.
The basic general reference books are [a11] and [a4].
References
| [a1] | R.J. Duffin, A.C. Schaeffer, "Khintchine's problem in metric diophantine approximation" Duke Math. J. , 8 (1941) pp. 243–255 |
| [a2] | P. Erdös, "On the distribution of convergents of almost all real numbers" J. Number Th. , 2 (1970) pp. 425–441 |
| [a3] | P.X. Gallagher, "Metric simultaneous diophantine approximation II" Mathematika , 12 (1965) pp. 123–127 |
| [a4] | G. Harman, "Metric number theory" , London Math. Soc. Monogr. , 18 , Clarendon Press (1998) |
| [a5] | G. Harman, "Some cases of the Duffin and Schaeffer conjecture" Quart. J. Math. Oxford , 41 : 2 (1990) pp. 395–404 |
| [a6] | G. Harman, "Metric diophantine approximation with two restricted variables III. Two prime numbers" J. Number Th. , 29 (1988) pp. 364–375 |
| [a7] | A. Khintchine, "Einige Saetze über Kettenbruche, mit Anwendungen auf die Theorie der Diophantischen Approximationen" Math. Ann. , 92 (1924) pp. 115–125 |
| [a8] | J. Lesca, "Sur les approximations diophantiennes a'une dimension" Doctoral Thesis Univ. Grenoble (1968) |
| [a9] | H. Nakada, G. Wagner, "Duffin–Schaeffer theorem of diophantine approximation for complex number" Astérisque , 198–200 (1991) pp. 259–263 |
| [a10] | A.D. Pollington, R.C. Vaughan, "The 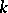 -dimensional Duffin and Schaeffer conjecture" Mathematika , 37 : 2 (1990) pp. 190–200 -dimensional Duffin and Schaeffer conjecture" Mathematika , 37 : 2 (1990) pp. 190–200 |
| [a11] | V.G. Sprindzuk, "Metric theory of diophantine approximations" , Winston&Wiley (1979) |
Duffin-Schaeffer conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Duffin-Schaeffer_conjecture&oldid=11508