Dual functions
Functions complementary in the sense of Young, i.e. strictly convex functions (cf. Convex function (of a real variable)) connected by the Legendre transform.
Comments
For certain real-valued non-decreasing functions defined on the positive half-line (including zero) there is a natural notion of an inverse. If  and
and  are such inverses to each other, the functions
are such inverses to each other, the functions  and
and  defined (on the positive half-line) by
defined (on the positive half-line) by
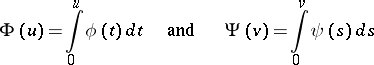 |
are said to be complementary in the sense of Young or Young-conjugate. For them Young's inequality holds:
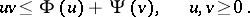 |
Associated with a pair  of non-vanishing functions complementary in the sense of Young and a
of non-vanishing functions complementary in the sense of Young and a  -finite measure, there is a pair
-finite measure, there is a pair 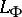 ,
, 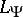 of complete normed spaces. These spaces, consisting of (equivalence classes of)
of complete normed spaces. These spaces, consisting of (equivalence classes of)  -measurable functions, are called Orlicz spaces (cf. Orlicz space). The Lebesgue spaces
-measurable functions, are called Orlicz spaces (cf. Orlicz space). The Lebesgue spaces  (cf. Lebesgue space) are particular cases of Orlicz spaces, cf. [a4].
(cf. Lebesgue space) are particular cases of Orlicz spaces, cf. [a4].
In a more abstract setting, the name dual functions is reminiscent of dual pair in duality theory and of dual problems in convex programming and optimal control (cf. Optimal control, mathematical theory of), but this name is rarely used in English: the most common name is (convex) conjugate functions (cf. Conjugate function).
Let 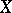 and
and  be two real vector spaces in separate duality with respect to a bilinear form
be two real vector spaces in separate duality with respect to a bilinear form 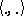 (the usual one if
(the usual one if  ), and let
), and let  be a mapping from
be a mapping from 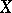 into
into 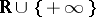 (if
(if 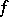 is only defined on a subset
is only defined on a subset  of
of 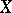 , set
, set  on
on  , the complement of
, the complement of 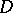 ). If
). If  is non-empty, the dual, or polar, or adjoint, or better conjugate function of
is non-empty, the dual, or polar, or adjoint, or better conjugate function of 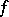 is the convex function
is the convex function 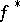 defined on
defined on 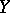 by
by
 |
The following result is a generalization of the geometric Hahn–Banach theorem on the bipolar of a set: the biconjugate function  of
of  is the greatest lower semi-continuous convex function bounded above by
is the greatest lower semi-continuous convex function bounded above by 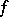 , and so is equal to
, and so is equal to 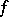 if and only if
if and only if 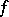 is a lower semi-continuous convex function (in which case
is a lower semi-continuous convex function (in which case 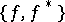 is called a pair of conjugate functions). The notion of conjugate function, which was introduced by W. Young in the case
is called a pair of conjugate functions). The notion of conjugate function, which was introduced by W. Young in the case  and by W. Fenchel in the case
and by W. Fenchel in the case 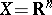 , is very important in convex analysis; it is closely related to the notion of subdifferential: if
, is very important in convex analysis; it is closely related to the notion of subdifferential: if  is convex and
is convex and 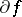 is its subdifferential, then for
is its subdifferential, then for 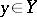 and
and 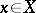 one has
one has
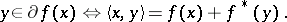 |
This can be written, if  is lower semi-continuous, as
is lower semi-continuous, as
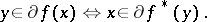 |
The mapping  is often called the Fenchel transform, sometimes with the name of Young or Legendre, or both, added. When
is often called the Fenchel transform, sometimes with the name of Young or Legendre, or both, added. When 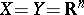 and
and  is sufficiently smooth as a convex function, it is a special case of the Legendre transform; on the other hand, it is also a special case of a Galois correspondence; these facts are of secondary importance in convex analysis. The notion of conjugate function plays a fundamental role in convex optimization. It is used to define the Lagrangian of some problem and the associated dual problem.
is sufficiently smooth as a convex function, it is a special case of the Legendre transform; on the other hand, it is also a special case of a Galois correspondence; these facts are of secondary importance in convex analysis. The notion of conjugate function plays a fundamental role in convex optimization. It is used to define the Lagrangian of some problem and the associated dual problem.
When  , a function
, a function 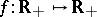 is called a Young function if it is a non-decreasing convex function such that
is called a Young function if it is a non-decreasing convex function such that  and
and 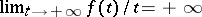 . The conjugate function
. The conjugate function  of a Young function
of a Young function 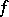 is still a Young function on
is still a Young function on  ; for example, when
; for example, when  with
with  , then
, then 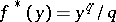 where
where 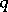 is the conjugate exponent of
is the conjugate exponent of  , i.e.
, i.e. 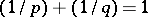 . Young functions are used to define Orlicz spaces (cf. Orlicz space), and pairs of conjugate Young functions are used to study the duality between them; more generally they help to establish various inequalities in measure theory (Burkholder inequalities in martingale theory, Chernov's inequality in classical probability theory, Kullback's inequality in statistics, etc.), via the easy to prove but fundamental Young inequality
. Young functions are used to define Orlicz spaces (cf. Orlicz space), and pairs of conjugate Young functions are used to study the duality between them; more generally they help to establish various inequalities in measure theory (Burkholder inequalities in martingale theory, Chernov's inequality in classical probability theory, Kullback's inequality in statistics, etc.), via the easy to prove but fundamental Young inequality
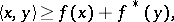 |
which enabled Young to solve a problem about Fourier transformation.
References
| [a1] | R.T. Rockafellar, "Conjugate duality and optimization" , Reg. Conf. Ser. Appl. Math. , SIAM (1974) |
| [a2] | J. Neveu, "Martingales à temps discret" , Masson (1972) |
| [a3] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , 2. Theory of martingales , North-Holland (1978–1988) (Translated from French) |
| [a4] | A.C. Zaanen, "Linear analysis" , North-Holland (1956) |
Dual functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dual_functions&oldid=12311