Dual category
to a category 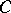
The category 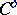 with the same objects as
with the same objects as 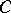 and with morphism sets
and with morphism sets 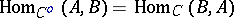 ( "reversal of arrows" ). Composition of two morphisms
( "reversal of arrows" ). Composition of two morphisms  and
and  in the category
in the category 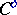 is defined as composition of
is defined as composition of  with
with  in
in 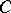 . The concepts and the statements in the category
. The concepts and the statements in the category 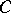 are replaced by dual concepts and statements in
are replaced by dual concepts and statements in 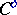 . Thus, the concept of an epimorphism is dual to the concept of a monomorphism; the concept of a projective object is dual to that of an injective object, that of the direct product to that of the direct sum, etc. A contravariant functor on
. Thus, the concept of an epimorphism is dual to the concept of a monomorphism; the concept of a projective object is dual to that of an injective object, that of the direct product to that of the direct sum, etc. A contravariant functor on 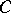 becomes covariant on
becomes covariant on 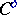 .
.
A dual category may sometimes have a direct realization; thus, the category of discrete Abelian groups is equivalent to the category dual to the category of compact Abelian groups (Pontryagin duality), while the category of affine schemes is equivalent to the category dual to the category of commutative rings with a unit element.
Comments
The dual category to a category 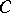 is also called the opposite category, and one also uses the notation
is also called the opposite category, and one also uses the notation 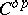 (see Category).
(see Category).
Dual category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dual_category&oldid=18831