Dual basis
to a basis 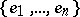 of a module
of a module  with respect to a form
with respect to a form 
A basis  of
of 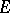 such that
such that
 |
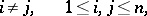 |
where  is a free
is a free 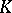 -module over a commutative ring
-module over a commutative ring 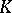 with a unit element, and
with a unit element, and  is a non-degenerate (non-singular) bilinear form on
is a non-degenerate (non-singular) bilinear form on 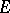 .
.
Let  be the dual module of
be the dual module of  , and let
, and let 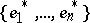 be the basis of
be the basis of 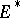 dual to the initial basis of
dual to the initial basis of 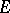 :
: 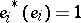 ,
, 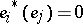 ,
,  . To each bilinear form
. To each bilinear form  on
on  there correspond mappings
there correspond mappings  , defined by the equations
, defined by the equations
 |
If the form  is non-singular,
is non-singular,  are isomorphisms, and vice versa. Here the basis
are isomorphisms, and vice versa. Here the basis  dual to
dual to  is distinguished by the following property:
is distinguished by the following property:
 |
Comments
A bilinear form  on
on  is non-degenerate (also called non-singular) if for all
is non-degenerate (also called non-singular) if for all 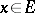 ,
, 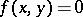 for all
for all 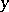 implies
implies 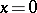 and for all
and for all 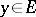 ,
, 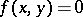 for all
for all  implies
implies  . Occasionally the terminology conjugate module (conjugate space) is used instead of dual module (dual space).
. Occasionally the terminology conjugate module (conjugate space) is used instead of dual module (dual space).
References
| [a1] | P.M. Cohn, "Algebra" , 1 , Wiley (1982) |
Dual basis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dual_basis&oldid=14785