Du Bois-Reymond lemma
From Encyclopedia of Mathematics
If 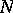 is a continuous function on the segment
is a continuous function on the segment 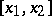 and if for all continuously-differentiable functions
and if for all continuously-differentiable functions 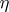 which vanish at
which vanish at 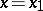 ,
, 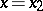 the relation
the relation
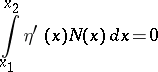 |
is valid, then 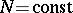 on
on 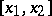 . Formulated by P. du Bois-Reymond [1].
. Formulated by P. du Bois-Reymond [1].
The du Bois-Reymond lemma is employed in the calculus of variations to derive the Euler equation in its integral form. In this proof it is not necessary to assume that the extremum of the functional is attained on a twice-differentiable curve; the assumption of continuous differentiability is sufficient.
References
| [1] | P. du Bois-Reymond, "Erläuterungen zu der Anfangsgründen der Variationsrechnung" Math. Ann. , 15 (1879) pp. 283–314 |
| [2] | M.A. Lavrent'ev, L.A. Lyusternik, "A course in variational calculus" , Moscow-Leningrad (1950) (In Russian) |
Comments
References
| [a1] | S. [S.V. Fomin] Fomine, "Commande optimale" , MIR (1982) (Translated from Russian) |
How to Cite This Entry:
Du Bois-Reymond lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Du_Bois-Reymond_lemma&oldid=18248
Du Bois-Reymond lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Du_Bois-Reymond_lemma&oldid=18248
This article was adapted from an original article by I.B. Vapnyarskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article