Double and dual numbers
Hypercomplex numbers of the form  , where
, where  and
and  are real numbers, and where the double numbers satisfy the relation
are real numbers, and where the double numbers satisfy the relation  , while the dual numbers satisfy the relation
, while the dual numbers satisfy the relation  (cf. Hypercomplex number). Addition of double and dual numbers is defined by
(cf. Hypercomplex number). Addition of double and dual numbers is defined by
 |
Multiplication of double numbers is defined by
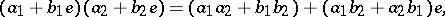 |
and that of dual numbers by
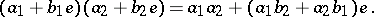 |
Complex numbers, double numbers and dual numbers are also called complex numbers of hyperbolic, elliptic and parabolic types, respectively. These numbers are sometimes used to represent motions in the three-dimensional spaces of Lobachevskii, Riemann and Euclid (see, for instance, Helical calculus).
Both double and dual numbers form two-dimensional (with base 1 and  ) associative-commutative algebras over the field of real numbers. As distinct from the field of complex numbers, these algebras comprise zero divisors, all these having the form
) associative-commutative algebras over the field of real numbers. As distinct from the field of complex numbers, these algebras comprise zero divisors, all these having the form 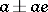 in the algebra of double numbers. The algebra of double numbers may be split into a direct sum of two real number fields. Hence yet another name for double numbers — splitting complex numbers. Double numbers have yet another appellation — paracomplex numbers. The algebra of dual numbers is considered not only over the field
in the algebra of double numbers. The algebra of double numbers may be split into a direct sum of two real number fields. Hence yet another name for double numbers — splitting complex numbers. Double numbers have yet another appellation — paracomplex numbers. The algebra of dual numbers is considered not only over the field  of real numbers, but also over an arbitrary field or commutative ring. Let
of real numbers, but also over an arbitrary field or commutative ring. Let  be a commutative ring and let
be a commutative ring and let 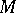 be an
be an  -module. The direct sum of
-module. The direct sum of 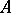 -modules
-modules 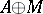 equipped with the multiplication
equipped with the multiplication
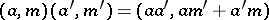 |
is a commutative 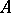 -algebra and is denoted by
-algebra and is denoted by  . It is known as the algebra of dual numbers with respect to the module
. It is known as the algebra of dual numbers with respect to the module 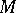 . The
. The 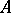 -module
-module  is identical with the ideal of the algebra
is identical with the ideal of the algebra 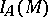 which is the kernel of the augmentation homomorphism
which is the kernel of the augmentation homomorphism
 |
The square  of this ideal is zero, while
of this ideal is zero, while 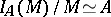 . If
. If  is a regular ring the converse is also true: If
is a regular ring the converse is also true: If 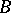 is an
is an  -algebra and
-algebra and  is an ideal in
is an ideal in  such that
such that  and
and 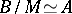 , then
, then  , where
, where 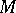 is regarded as an
is regarded as an  -module [4].
-module [4].
If  , the algebra
, the algebra  (then denoted by
(then denoted by 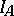 ) is isomorphic to the quotient algebra of the algebra of polynomials
) is isomorphic to the quotient algebra of the algebra of polynomials  by the ideal
by the ideal 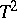 . Many properties of an
. Many properties of an 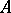 -module may be formulated as properties of the algebra
-module may be formulated as properties of the algebra  ; as a result, many problems on
; as a result, many problems on 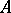 -modules can be reduced to corresponding problems in the theory of rings [2].
-modules can be reduced to corresponding problems in the theory of rings [2].
Let 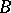 be an arbitrary
be an arbitrary 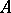 -algebra, let
-algebra, let  be a homomorphism and let
be a homomorphism and let 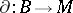 be a derivation (cf. Derivation in a ring) of
be a derivation (cf. Derivation in a ring) of  with values in the
with values in the 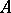 -module
-module 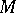 , regarded as a
, regarded as a 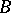 -module with respect to the homomorphism
-module with respect to the homomorphism 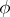 . The mapping
. The mapping 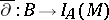 (
( ) will then be a homomorphism of
) will then be a homomorphism of 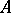 -algebras. Conversely, for any homomorphism of
-algebras. Conversely, for any homomorphism of 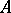 -algebras
-algebras  the composition
the composition 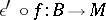 , where
, where 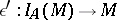 is the projection of
is the projection of  onto
onto 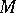 , is an
, is an  -derivation of
-derivation of 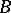 with values in
with values in  , regarded as a
, regarded as a  -module with respect to the homomorphism
-module with respect to the homomorphism  . This property of double and dual numbers is utilized for the description of the tangent space to an arbitrary functor in the category of schemes [1], [3].
. This property of double and dual numbers is utilized for the description of the tangent space to an arbitrary functor in the category of schemes [1], [3].
References
| [1] | D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) |
| [2] | R. Fossum, P.A. Griffith, I. Reiten, "Trivial extensions of Abelian categories. Homological algebra of trivial extensions of Abelian categories with applications to ring theory" , Springer (1975) |
| [3] | M. Demazure, A. Grothendieck, "Schémas en groupes I" , Lect. notes in math. , 151–153 , Springer (1970) |
| [4] | S. Lichtenbaum, M. Schlessinger, "The cotangent complex of a morphism" Trans. Amer. Math. Soc. , 128 : 1 (1967) pp. 41–70 |
Comments
An old-fashioned term for an associative algebra 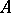 with unit element over
with unit element over  is system of hypercomplex numbers, and an element of
is system of hypercomplex numbers, and an element of 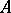 is then called a hypercomplex number. There are (up to isomorphism) precisely three of these algebras of dimension 2: the complex numbers, the dual numbers and the double numbers.
is then called a hypercomplex number. There are (up to isomorphism) precisely three of these algebras of dimension 2: the complex numbers, the dual numbers and the double numbers.
References
| [a1] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , Masson (1970) |
Double and dual numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Double_and_dual_numbers&oldid=46769