Double-periodic function
A single-valued analytic function  with only isolated singularities on the entire finite complex
with only isolated singularities on the entire finite complex  -plane, and such that there exists two numbers
-plane, and such that there exists two numbers  whose quotient is not a real number and which are periods of
whose quotient is not a real number and which are periods of  , i.e.
, i.e.  are such that the identity
are such that the identity
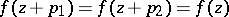 |
is valid. (If  is real and rational,
is real and rational,  is a simply-periodic function; if
is a simply-periodic function; if 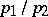 is real and irrational,
is real and irrational,  .) All numbers of the form
.) All numbers of the form  where
where 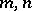 are integers are also periods of
are integers are also periods of 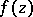 . All periods of a given double-periodic function form a discrete Abelian group with respect to addition, known as the period group (or the period module), a basis of which (a period basis) is constituted by two primitive periods
. All periods of a given double-periodic function form a discrete Abelian group with respect to addition, known as the period group (or the period module), a basis of which (a period basis) is constituted by two primitive periods 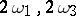 ,
, 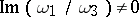 . All remaining periods of this double-periodic function may be represented in the form
. All remaining periods of this double-periodic function may be represented in the form 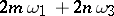 where
where  are integers. Analytic functions of one complex variable with more than two primitive periods do not exist, except for constants.
are integers. Analytic functions of one complex variable with more than two primitive periods do not exist, except for constants.
The points of the form 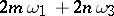 where
where 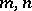 are integers form the period lattice (subdividing the entire
are integers form the period lattice (subdividing the entire  -plane into period parallelograms). Points (numbers)
-plane into period parallelograms). Points (numbers)  ,
,  for which
for which
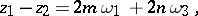 |
are said to be congruent (comparable with respect to the period module). At congruent points the double-periodic function  assumes the same value, so that it is sufficient to study the behaviour of
assumes the same value, so that it is sufficient to study the behaviour of  in some basic period parallelogram. This is usually the set of points
in some basic period parallelogram. This is usually the set of points
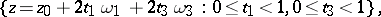 |
i.e. the parallelogram with vertices
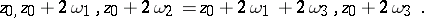 |
A non-constant double-periodic function that is regular in the entire basic period parallelogram does not exist. Meromorphic double-periodic functions are called elliptic functions (cf. Elliptic function). The generalization of the concept of an elliptic function to include functions 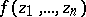 of
of  complex variables are called Abelian functions (cf. Abelian function).
complex variables are called Abelian functions (cf. Abelian function).
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 3 , Chelsea (1977) pp. Chapt. 4 (Translated from Russian) |
| [2] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , 2 , Springer (1968) |
| [3] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , 2 , Cambridge Univ. Press (1952) pp. Chapt. 20 |
| [4] | N.I. Akhiezer, "Elements of the theory of elliptic functions" , Amer. Math. Soc. (1990) (Translated from Russian) |
Comments
References
| [a1] | S. Lang, "Elliptic functions" , Addison-Wesley (1973) |
Double-periodic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Double-periodic_function&oldid=15821