Divisor (algebraic geometry)

A generalization of the concept of a divisor of an element of a commutative ring. First introduced by E.E. Kummer [1] under the name of "ideal divisorideal divisor" in his studies on cyclotomic fields.

The theory of divisors for an integral commutative ring 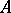with a unit element consists in constructing a homomorphism 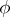from the multiplicative semi-group 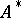of non-zero elements of 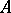into some semi-group 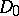with unique factorization, the elements of which are known as (integral) divisors of the ring 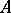. The theory of divisors makes it possible to reduce a series of problems connected with prime factorization in 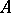, where this factorization may be not unique, to the problem of prime factorization in 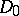. The image 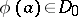of an element 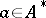is denoted by 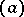and is called the principal divisor of the element . 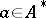One says that is divisible by the divisor 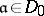if divides in .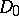

More exactly, let 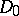be a free Abelian semi-group with a unit element, the free generators of which are known as prime divisors, and let a homomorphism 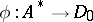be given. The homomorphism 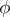defines a theory of divisors of the ring 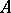if it satisfies the following conditions.

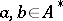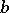1) For the element divides in 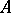if and only if 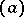divides 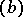in .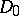

2) For any ,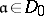

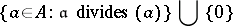is an ideal of .

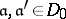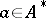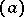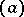3) If and if, for any , is divisible by if and only if is divisible by 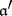, then .

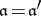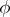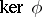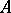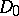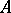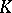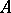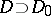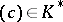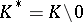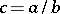If a homomorphism exists, it is uniquely determined, up to an isomorphism, by the conditions just listed. The kernel coincides with the group of unit elements of . The elements of are called positive divisors of . Let be the field of quotients of , and let be the free Abelian group generated by the set of prime divisors. Then for any , , it is possible to define a principal divisor . If where 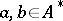, then 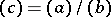. The elements of the group 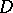are known as fractional divisors (or, simply, divisors) of 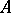(or of ). 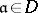Any divisor may be written in the form

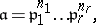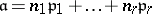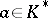where is a prime divisor. In additive notation: . If and 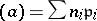, the mapping 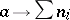is a discrete valuation on 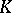, and is known as the essential valuation of 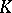. The homomorphism 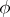is extended to a homomorphism 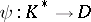, where 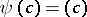, contained in the exact sequence

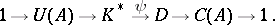Here 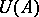is the group of invertible elements of 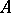, while the group 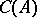is called the divisor class group of (or of 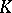). Two divisors which belong to the same equivalence class by the subgroup of principal divisors are called equivalent (in algebraic geometry, where a large number of other divisor equivalences are considered, this equivalence is known as linear).

The theory of divisors is valid for any Dedekind ring, in particular for rings of integral elements in algebraic number fields, and the elements of are in one-to-one correspondence with the non-zero ideals of the ring 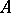(to the divisor corresponds the ideal of all elements of 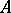that are divisible by ). This is why, in a Dedekind ring, the group of divisors is also called the group of ideals, while the divisor class group is called the ideal class group.

The divisor class group of an algebraic number field is finite, and many problems in algebraic number theory involve the computation of its order (the number of classes) and structure [2].

More generally, the theory of divisors is valid for Krull rings (cf. Krull ring, [11]). In such a case the role of 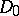is played by the semi-group of divisorial ideals (cf. Divisorial ideal) of the ring, while the part of 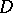is played by the group of fractional divisorial ideals.

The concept of a Weil divisor is a generalization of the concept of a fractional divisorial ideal of a commutative ring to algebraic varieties or analytic spaces . The name Weil divisor is given to integral formal finite linear combinations 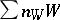of irreducible closed subspaces 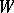in 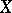of codimension 1. A Weil divisor is called positive, or effective, if all 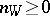. All Weil divisors form a group 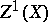(the group of Weil divisors). If 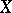is a smooth algebraic variety, the concept of a Weil divisor coincides with that of an algebraic cycle of codimension 1.

If 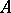is a Noetherian Krull ring, each prime divisorial ideal 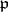in 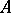defines a subspace 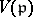of codimension 1 in the scheme 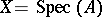, while each divisor 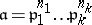may thus be identified with the Weil divisor .

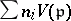Let 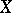be a normal scheme and let 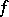be a rational (meromorphic in the analytic case) function on 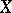. A principal Weil divisor is defined canonically:

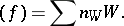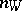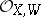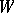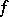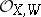Here is the value of the discrete valuation of the ring of the subvariety on the representative of in . If

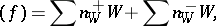where 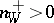and 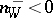, the Weil divisor 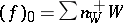is known as the divisor of the zeros, while 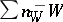is known as the divisor of the poles of the function 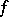. The set of principal Weil divisors is a subgroup 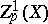of the group 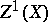. The quotient group 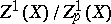is denoted by 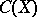and is known as the divisor class group of the scheme 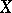. If 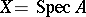, where 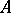is a Noetherian Krull ring, 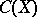coincides with the divisor class group of the ring .

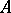Let 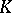be an algebraic function field. A divisor of 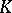is sometimes defined as a formal integral combination of discrete valuations of rank 1 o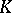f . If 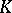is a field of algebraic functions in one variable, each such divisor may be identified with the Weil divisor of its complete non-singular model.

Let 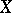be a regular scheme or a complex variety and let 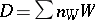be a Weil divisor. For any point 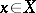there exists an open neighbourhood 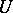such that the restriction of 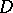on ,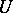

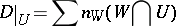is the principal divisor 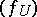for a certain meromorphic functi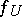on on 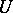. The function 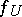is uniquely defined, up to an invertible function on 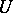, and is known as the local equation of the divisor 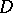in the neighbourhood 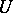, while the correspondence 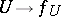defines a section of the sheaf 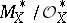. In general, a Cartier divisor on a ringed space 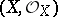is defined as a global section of the sheaf 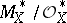of germs of divisors. Here 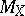denotes the sheaf of germs of meromorphic (or rational) functions on 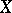, i.e. 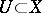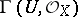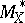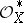the sheaf which brings into correspondence each open with the total quotient ring of the ring , while and are the sheaves of invertible elements in and 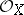, respectively. A Cartier divisor may be defined by a selection of local equations

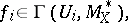where 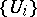is an open covering of 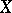, and the functions 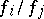should be a section of the sheaf 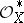over 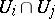. In particular, a meromorphic function 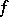defines a divisor 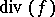known as a principal divisor. The set of 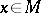such that 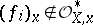is called the support of the divisor. The Cartier divisors form an Abelian group 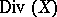, while the principal divisors form a subgroup of it, 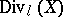. Each divisor 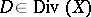defines an invertible sheaf 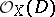contained in : If 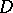is represented by the local equations 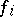on the covering 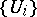, then

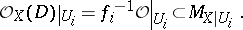The correspondence 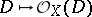is a homomorphism of the group 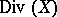into the Picard group 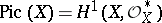. This homomorphism is included in the exact sequence

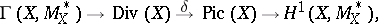which is obtained from the exact sequence of sheaves

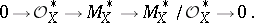Thus, 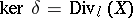. If 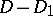is a principal divisor, 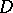and 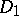are said to be linearly equivalent. If 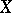is a quasi-projective algebraic variety or a complex Stein space, the homomorphism 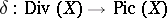is surjective and induces an isomorphism of the group of classes of linearly equivalent divisors 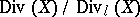onto the Picard group .

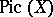If 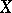is a complex space, the problem arises as to when a given divisor is a principal divisor; this is the so-called second Cousin problem (cf. Cousin problems). For example, the divisor class group on a complex Stein space is trivial if and only if .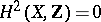

A divisor 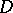is said to be effective (or positive) if 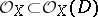. In such a case 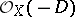is a sheaf of ideals in 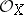; the support of a divisor 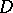with structure sheaf 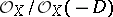forms a subspace in 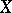, which is also denoted by .

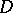For a normal Noetherian scheme or a normal analytic space 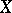there is a natural homomorphism:

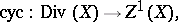mapping 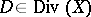into 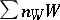, where 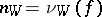and where 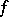is a local equation of 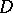in the neighbourhood 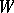, while 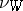is the discrete valuation corresponding to 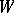[3]. The homomorphism cyc is injective and maps effective divisors to effective cycles; cyc is bijective if and only if 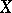is locally factorial (e.g. when 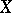is a non-singular scheme or an analytic manifold). If cyc is bijective, Weil and Cartier divisors coincide.

Let 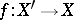be a morphism of schemes which is flat in codimension 1. Then, for any Cartier or Weil divisor 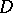on 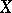the inverse image 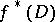is defined; also, 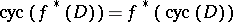. The mapping 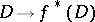is a homomorphism of groups which maps principal divisors to principal ones, and thus defines a homomorphism of groups

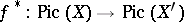(respectively,

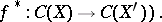If 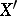is an open set in whose codimension of the complement is at least 2 and if 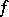is the imbedding of 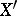into 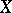, then 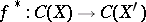is an isomorphism, while 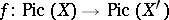is an isomorphism if the scheme 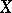is locally factorial.

Let 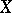be a smooth projective variety over 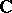. Any divisor 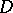on 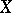defines a homology class

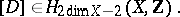The cohomology class which is Poincaré dual to 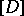is identical with the Chern class 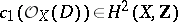of the invertible sheaf 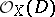. Thus there appears a homological equivalence on 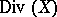. There exists a theory of intersections of divisors [7], leading to the concept of algebraic equivalence of divisors (cf. Algebraic cycle). The group

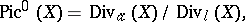where denotes the group of divisors which are algebraically equivalent to zero, is naturally provided with the structure of an Abelian variety (the Picard variety; if 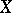is a curve, it is also called the Jacobi variety of 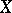). The group 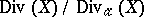, known as the Néron–Severi group, has a finite number of generators. The last two facts also apply to algebraic varieties over an arbitrary field.

If 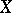is a one-dimensional complex manifold (a Riemann surface), a divisor on 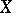is a finite linear combination

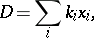where 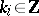, 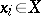. The number 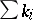is called the degree of the divisor 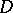. For a compact Riemann surface of genus 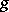the group of divisor classes of degree zero is a -dimensional Abelian variety and is identical with the Picard variety (or with the Jacobi variety). If 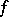is a meromorphic function on , a principal divisor is

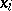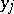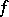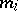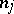where are the zeros and are the poles of and , are their multiplicities. Then 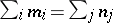, i.e. a principal divisor has degree 0. A divisor of degree 0 on 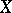is principal if and only if there exists a singular one-dimensional chain 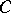such that

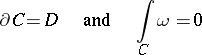for all holomorphic forms 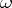of degree 1 on 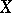(Abel's theorem). See also Abelian differential.

References

[1]	E.E. Kummer, "Ueber die Zerlegung der aus Wurzeln der Einheit gebildeten complexe Zahlen in ihre Primfaktoren" J. Reine Angew. Math. , 35 (1847) pp. 327–367
[2]	Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966)
[3]	A. Weil, "Introduction à l'Aeetude des variétés kahlériennes" , Hermann (1958)
[4]	P. Cartier, "Questions de rationalité des diviseurs en géometrie algébrique" Bull. Soc. Math. France , 86 (1958) pp. 177–251
[5]	A. Grothendieck, "Eléments de géometrie algébrique IV. Etude locale des schémas et des morphismes des schémas" Publ. Math. IHES : 32 (1967)
[6]	D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966)
[7]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian)
[8]	C. Chevalley, "Introduction to the theory of algebraic functions of one variable" , Amer. Math. Soc. (1951)
[9]	R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965)
[10]	S.S. Chern, "Complex manifolds without potential theory" , Springer (1979)
[11]	N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French)
[12]	G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957)

References

[a1]	R. Hartshorne, "Algebraic geometry" , Springer (1977)
[a2]	P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) pp. 178; 674; 179; 349; 525; 532; 535; 632; 743
[a3]	R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980)