Division ring
From Encyclopedia of Mathematics
division ring
A (not necessarily associative) ring in which the equations
 |
are solvable for any two elements  and
and 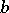 , where
, where 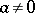 . If the solutions of these equations are uniquely determined, then the ring is called a quasi-division ring. In contrast to an arbitrary division ring, a quasi-division ring cannot have divisors of zero (cf. Zero divisor); the non-zero elements of a quasi-division ring form a quasi-group with respect to multiplication. Each (not necessarily associative) ring without divisors of zero can be imbedded in a quasi-division ring. An associative division ring is an (associative) skew-field. See also Division algebra.
. If the solutions of these equations are uniquely determined, then the ring is called a quasi-division ring. In contrast to an arbitrary division ring, a quasi-division ring cannot have divisors of zero (cf. Zero divisor); the non-zero elements of a quasi-division ring form a quasi-group with respect to multiplication. Each (not necessarily associative) ring without divisors of zero can be imbedded in a quasi-division ring. An associative division ring is an (associative) skew-field. See also Division algebra.
References
| [1] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
Comments
References
| [a1] | N. Jacobson, "The theory of rings" , Amer. Math. Soc. (1943) |
How to Cite This Entry:
Division ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Division_ring&oldid=17857
Division ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Division_ring&oldid=17857
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article