Division algebra
An algebra  over a field
over a field  such that for any elements
such that for any elements  and
and  the equations
the equations  ,
,  are solvable in
are solvable in  . An associative division algebra, considered as a ring, is a skew-field, its centre
. An associative division algebra, considered as a ring, is a skew-field, its centre  is a field, and
is a field, and  . If
. If 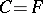 , the division algebra
, the division algebra 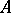 is called a central division algebra. Finite-dimensional central associative division algebras over
is called a central division algebra. Finite-dimensional central associative division algebras over 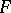 may be identified, up to an isomorphism, with the elements of the Brauer group
may be identified, up to an isomorphism, with the elements of the Brauer group 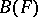 of the field
of the field 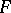 . Let
. Let 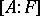 denote the dimension of
denote the dimension of  over
over 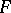 . If
. If  and if
and if  is the maximal subfield in
is the maximal subfield in  (
(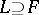 ), then
), then  . According to the Frobenius theorem, all associative finite-dimensional division algebras over the field of real numbers
. According to the Frobenius theorem, all associative finite-dimensional division algebras over the field of real numbers 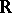 are exhausted by
are exhausted by 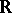 itself, the field of complex numbers, and the quaternion algebra. For this reason the group
itself, the field of complex numbers, and the quaternion algebra. For this reason the group 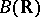 is cyclic of order two. If the associativity requirement is dropped, there is yet another example of a division algebra over the field of real numbers: the Cayley–Dickson algebra. This algebra is alternative, and its dimension over
is cyclic of order two. If the associativity requirement is dropped, there is yet another example of a division algebra over the field of real numbers: the Cayley–Dickson algebra. This algebra is alternative, and its dimension over 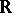 is 8. If
is 8. If 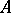 is a finite-dimensional (not necessarily associative) division algebra over
is a finite-dimensional (not necessarily associative) division algebra over 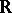 , then
, then  has one of the values 1, 2, 4, or 8.
has one of the values 1, 2, 4, or 8.
References
| [1] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
| [2] | A.A. Albert, "Structure of algebras" , Amer. Math. Soc. (1939) |
| [3] | I.N. Herstein, "Noncommutative rings" , Math. Assoc. Amer. (1968) |
| [4] | J.F. Adams, "On the non-existence of elements of Hopf invariant one" Ann. of Math. , 72 : 1 (1960) pp. 20–104 |
Comments
Over a finite field every finite-dimensional central division algebra is automatically commutative. For infinite-dimensional division algebras the situation is quite different, because a result of Mokar–Limonov states that such an algebra contains a free algebra in two variables.
If a finite-dimensional central division algebra  contains a maximal commutative subfield
contains a maximal commutative subfield 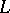 which is a Galois extension of
which is a Galois extension of  , then
, then 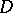 is a cross product of
is a cross product of  and
and 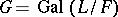 in the sense that
in the sense that 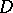 is the free
is the free  -module generated by
-module generated by  with product determined by:
with product determined by:
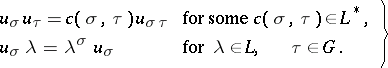 | (a1) |
Associativity of 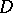 entails that
entails that 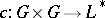 represents an element of
represents an element of 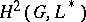 (the second Galois cohomology group). One of the basic problems in algebra was formulated by A. Albert (1931): Is every finite-dimensional central division algebra necessarily a cross product? In 1972, S. Amitsur provided a counter-example using properties of generic division algebras resulting from the theory of PI-algebras (see PI-algebra, [a2]). Other examples of division algebras were obtain by F. van Ostaeyen (1972 Thesis, cf. [a3]), i.e. generic cross products, a notion generalized by Amitsur and D. Saltman (1978), describing all cross product division algebras for a given group
(the second Galois cohomology group). One of the basic problems in algebra was formulated by A. Albert (1931): Is every finite-dimensional central division algebra necessarily a cross product? In 1972, S. Amitsur provided a counter-example using properties of generic division algebras resulting from the theory of PI-algebras (see PI-algebra, [a2]). Other examples of division algebras were obtain by F. van Ostaeyen (1972 Thesis, cf. [a3]), i.e. generic cross products, a notion generalized by Amitsur and D. Saltman (1978), describing all cross product division algebras for a given group 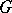 over the field
over the field 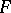 as reductions of a generic division algebra.
as reductions of a generic division algebra.
References
| [a1] | A.H. Schofield, "Representations of rings over skew fields" , London Math. Soc. (1986) |
| [a2] | N. Jacobson, "PI algebras. An introduction" , Springer (1975) |
| [a3] | F. van Oystaeyen, "Prime spectra in non-commutative algebra" , Springer (1975) |
Division algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Division_algebra&oldid=16477