Divergent series
A series for which the sequence of partial sums does not have a finite limit. For example, the series
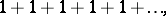 |
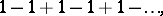 |
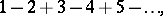 |
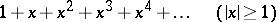 |
are divergent.
Divergent series first appeared in the works of mathematicians of the 17th century and 18th century. L. Euler first came to the conclusion that the question must be posed, not what the sum is equal to, but how to define the sum of a divergent series, and he found an approach to the solution of this problem close to the modern one. Up till the end of the 19th century, divergent series did not find any application and were almost forgotten. Towards the end of the 19th century an accumulation of various facts in mathematical analysis re-awakened interest in divergent series. The question was raised about the possibility of summing series in a sense different from the usual one.
Examples.
1) If one multiplies two series
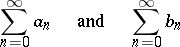 |
that converge to  and
and  , respectively, then the resulting series
, respectively, then the resulting series
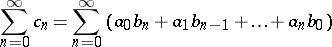 | (1) |
can be divergent. However, if one defines the sum of the series (1) not as the limit of the partial sums  , but as
, but as
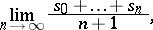 | (2) |
then in this sense the series (1) will always converge (i.e. the limit (2) exists) and its sum in this sense is equal to  .
.
2) The Fourier series of a function  continuous at a point
continuous at a point  (or having a discontinuity of the first kind) can diverge at this point. If the sum of the series is defined by formula (2), then in this sense the Fourier series of such a function will always converge and its sum in this sense will equal
(or having a discontinuity of the first kind) can diverge at this point. If the sum of the series is defined by formula (2), then in this sense the Fourier series of such a function will always converge and its sum in this sense will equal 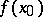 (or
(or  ).
).
3) The power series
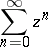 | (3) |
converges for  to the sum
to the sum 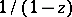 and diverges for
and diverges for  . If one defines the sum of the series to be
. If one defines the sum of the series to be
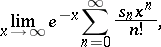 | (4) |
where the  are the partial sums of the series (3), then in this sense the series (3) will converge for all
are the partial sums of the series (3), then in this sense the series (3) will converge for all  with
with 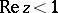 , and its sum is the function
, and its sum is the function  .
.
To generalize the concept of a sum to the case of a divergent series, one takes some operator or rule which assigns a specific number to a divergent series, called its sum (in this definition). Such a rule is called a summation method (cf. Summation methods). Thus, the rule described in Example 1) is called summation by arithmetical averages (see Cesàro summation methods). The rule given in Example 2) is called the Borel summation method.
See also Summation of divergent series.
References
| [1] | E. Borel, "Leçons sur les series divergentes" , Gauthier-Villars (1928) |
| [2] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [3] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
| [4] | A. Peyerimhoff, "Lectures on summability" , Springer (1969) |
| [5] | K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) ((Incomplete English translation: Blackie, 1928)) |
| [6] | K. Zeller, W. Beekmann, "Theorie der Limitierungsverfahren" , Springer (1970) |
Comments
Instead of "summation method" the phrase "summability methodsummability method" is often used.
Divergent series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Divergent_series&oldid=12874