Divergence theorem
A formula in the integral calculus of functions in several variables that establishes a link between an  -fold integral over a domain and an
-fold integral over a domain and an 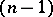 -fold integral over its boundary. Let the functions
-fold integral over its boundary. Let the functions 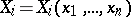 and their partial derivatives
and their partial derivatives 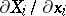 ,
,  , be Lebesgue integrable in a bounded domain
, be Lebesgue integrable in a bounded domain 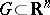 whose boundary
whose boundary 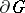 is the union of a finite set of piecewise-smooth
is the union of a finite set of piecewise-smooth 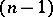 -dimensional hypersurfaces oriented using the exterior normal
-dimensional hypersurfaces oriented using the exterior normal  . The Ostrogradski formula then takes the form
. The Ostrogradski formula then takes the form
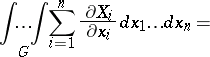 | (1) |
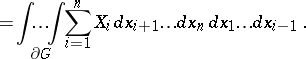 |
If 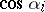 ,
, 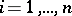 , are the direction cosines of the exterior normals
, are the direction cosines of the exterior normals  of the hypersurfaces forming the boundary
of the hypersurfaces forming the boundary 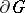 of
of 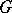 , then formula (1) can be expressed in the form
, then formula (1) can be expressed in the form
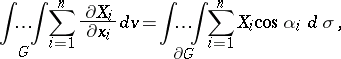 | (2) |
where 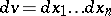 is the
is the  -dimensional volume element in
-dimensional volume element in 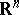 while
while 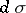 is the
is the 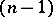 -dimensional volume element on
-dimensional volume element on 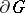 .
.
In terms of the vector field 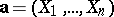 , the formulas (1) and (2) signify the equality of the integral of the divergence of this field over the domain
, the formulas (1) and (2) signify the equality of the integral of the divergence of this field over the domain 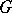 to its flux (see Flux of a vector field) over the boundary of
to its flux (see Flux of a vector field) over the boundary of 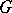 :
:
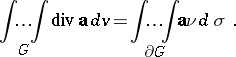 |
For smooth functions, the formula was first obtained for the  -dimensional case by M.V. Ostrogradski in 1828 (published in 1831, see [1]). He later extended it (1834) to cover
-dimensional case by M.V. Ostrogradski in 1828 (published in 1831, see [1]). He later extended it (1834) to cover  -fold integrals for an arbitrary natural
-fold integrals for an arbitrary natural  (published in 1838, see [2]). Using this formula, Ostrogradski found an expression for the derivative with respect to a parameter of an
(published in 1838, see [2]). Using this formula, Ostrogradski found an expression for the derivative with respect to a parameter of an  -fold integral with variable limits, and obtained a formula for the variation of an
-fold integral with variable limits, and obtained a formula for the variation of an  -fold integral; in one particular case, where
-fold integral; in one particular case, where 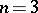 , the formula was obtained by C.F. Gauss in 1813, for this reason it is also sometimes called the Ostrogradski–Gauss formula. A generalization of this formula is the Stokes formula for manifolds with boundary.
, the formula was obtained by C.F. Gauss in 1813, for this reason it is also sometimes called the Ostrogradski–Gauss formula. A generalization of this formula is the Stokes formula for manifolds with boundary.
References
| [1] | M.V. Ostrogradski, Mém. Acad. Sci. St. Petersbourg. Sér. 6. Sci. Math. Phys. et Naturelles , 1 (1831) pp. 117–122 |
| [2] | M.V. Ostrogradski, Mém. Acad. Sci. St. Petersbourg. Sér. 6. Sci. Math. Phys. et Naturelles , 1 (1838) pp. 35–58 |
Comments
The result embodied in formula (2) above is most often known as the divergence theorem. It is (finally) equivalent to the Gauss formula (Gauss integral formula)
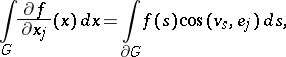 |
where 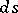 is the surface element for
is the surface element for  ,
, 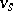 is the outward pointing unit normal at
is the outward pointing unit normal at 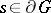 , and
, and 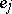 is the
is the 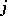 -th standard unit vector.
-th standard unit vector.
References
| [a1] | H. Triebel, "Analysis and mathematical physics" , Reidel (1986) pp. Sect. 9.3.1 |
| [a2] | A.M. Krall, "Applied analysis" , Reidel (1986) pp. 380 |
| [a3] | A.P. Wills, "Vector analysis with an introduction to tensor analysis" , Dover, reprint (1958) pp. 97ff |
| [a4] | C. von Westenholz, "Differential forms in mathematical physics" , North-Holland (1981) pp. 286ff |
Divergence theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Divergence_theorem&oldid=12667