Distributivity
distributivity law, distributive property, of one operation with respect to another
The property of a pair of binary algebraic operations (cf. Algebraic operation), expressed by one of the following identities:
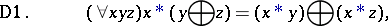 |
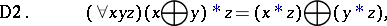 |
where  are the symbols of the binary operations, and
are the symbols of the binary operations, and  are object variables. If in a set
are object variables. If in a set  two specific binary operations
two specific binary operations  ,
,  are defined, i.e. two mappings
are defined, i.e. two mappings
 |
are given, and the symbols  are interpreted as the symbols of the respective operations
are interpreted as the symbols of the respective operations 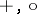 in
in 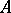 , one can speak of the truth or falsehood of each one of the formulas D1 and D2 in
, one can speak of the truth or falsehood of each one of the formulas D1 and D2 in 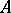 . If both these formulas are true in
. If both these formulas are true in 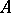 , the operation
, the operation  is called distributive with respect to the operation
is called distributive with respect to the operation 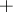 in
in 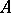 .
.
Comments
I.e., in 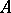 the operation
the operation  is distributive with respect to
is distributive with respect to 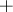 if for all
if for all 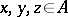 one has
one has 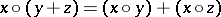 and
and 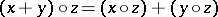 .
.
For example, multiplication is distributive with respect to addition in the set of real numbers and in the set of integers.
Distributivity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Distributivity&oldid=14448