Distributive quasi-group
A quasi-group which satisfies the left and the right distributive laws:  ,
,  . In quasi-groups these two laws are independent of each other (there are left-distributive quasi-groups which are not right-distributive [1]). As an example of a distributive quasi-group one may quote the set
. In quasi-groups these two laws are independent of each other (there are left-distributive quasi-groups which are not right-distributive [1]). As an example of a distributive quasi-group one may quote the set  of rational numbers with the operation
of rational numbers with the operation  . Any idempotent medial quasi-group (i.e. a quasi-group
. Any idempotent medial quasi-group (i.e. a quasi-group  in which the relations
in which the relations  and
and  are valid for all
are valid for all  ) is distributive. In the general case every distributive quasi-group
) is distributive. In the general case every distributive quasi-group  is isotopic (cf. Isotopy) to a commutative Moufang loop [3]. Parastrophies (quasi-groups with respect to inverse operations, cf. Quasi-group) of distributive quasi-groups are also distributive and are isotopic to the same commutative Moufang loop. If four elements
is isotopic (cf. Isotopy) to a commutative Moufang loop [3]. Parastrophies (quasi-groups with respect to inverse operations, cf. Quasi-group) of distributive quasi-groups are also distributive and are isotopic to the same commutative Moufang loop. If four elements 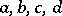 in a distributive quasi-group are connected by the medial law:
in a distributive quasi-group are connected by the medial law: 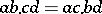 , they generate a medial sub-quasi-group. In particular, any three elements of a distributive quasi-group generate a medial sub-quasi-group. In a sub-quasi-group the translations are automorphisms, and in a certain sense a distributive quasi-group is homogeneous: No element, and no sub-quasi-group, is distinguished. The group generated by all right translations of a finite distributive quasi-group is solvable [4].
, they generate a medial sub-quasi-group. In particular, any three elements of a distributive quasi-group generate a medial sub-quasi-group. In a sub-quasi-group the translations are automorphisms, and in a certain sense a distributive quasi-group is homogeneous: No element, and no sub-quasi-group, is distinguished. The group generated by all right translations of a finite distributive quasi-group is solvable [4].
References
| [1] | Sh. Stein, "On a construction of Hosszú" Publ. Math. Debrecen , 6 : 1–2 (1959) pp. 10–14 |
| [2] | V.D. Belousov, "The structure of distributive quasigroups" Mat. Sb. , 50 : 3 (1960) pp. 267–298 (In Russian) |
| [3] | V.D. Belousov, "Foundations of the theory of quasi-groups and loops" , Moscow (1967) (In Russian) |
| [4] | B. Fischer, "Distributive Quasigruppen endlicher Ordnung" Math. Z. , 83 : 4 (1964) pp. 267–303 |
Comments
In [a1] it is shown that a quasi-group of order 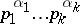 , with
, with  distinct prime numbers and
distinct prime numbers and  non-negative integers, is isomorphic to the direct product of distributive quasi-groups
non-negative integers, is isomorphic to the direct product of distributive quasi-groups 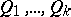 , where
, where 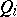 has order
has order 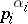 and is Abelian (i.e. satisfies
and is Abelian (i.e. satisfies 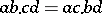 ) for
) for  .
.
References
| [a1] | V.M. Galkin, "Finite distributive quasigroups" Math. Notes , 24 (1978) pp. 525–526 Mat. Zametki , 24 (1978) pp. 39–41; 141 |
Distributive quasi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Distributive_quasi-group&oldid=13856