Distributive lattice
A lattice in which the equation
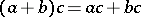 |
holds. This equation is equivalent to both
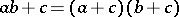 |
and
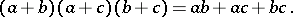 |
Distributive lattices are characterized by the fact that all their convex sublattices can occur as congruence classes. Any distributive lattice is isomorphic to a lattice of (not necessarily all) subsets of some set. An important special case of such lattices are Boolean algebras (cf. Boolean algebra). For any finite set  in a distributive lattice the following equalities are valid:
in a distributive lattice the following equalities are valid:
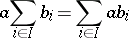 |
and
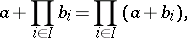 |
as well as
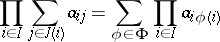 |
and
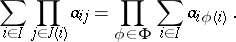 |
Here the  are finite sets and
are finite sets and 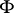 is the set of all single-valued functions
is the set of all single-valued functions 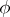 from
from  into
into 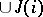 such
such  for each
for each 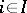 . In a complete lattice the above equations also have a meaning if the sets
. In a complete lattice the above equations also have a meaning if the sets  and
and 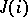 are infinite. However, they do not follow from the distributive law. Distributive complete lattices (cf. Complete lattice) which satisfy the two last-mentioned identities for all sets
are infinite. However, they do not follow from the distributive law. Distributive complete lattices (cf. Complete lattice) which satisfy the two last-mentioned identities for all sets  and
and 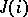 are called completely distributive.
are called completely distributive.
References
| [1] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [2] | L.A. Skornyakov, "Elements of lattice theory" , Hindushtan Publ. Comp. (1977) (Translated from Russian) |
| [3] | G. Grätzer, "General lattice theory" , Birkhäuser (1978) (Original: Lattice theory. First concepts and distributive lattices. Freeman, 1978) |
Comments
The distributive property of lattices may be characterized by the presence of enough prime filters: A lattice  is distributive if and only if its prime filters separate its points, or, equivalently, if, given
is distributive if and only if its prime filters separate its points, or, equivalently, if, given 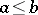 in
in 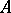 , there exists a lattice homomorphism
, there exists a lattice homomorphism 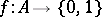 with
with 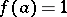 and
and  , [a1]. In the study of distributive lattices, their topological representation plays an important role; this was first established by M.H. Stone [a2], and reformulated in more convenient terms by H.A. Priestley [a3] — both versions generalize the Stone duality for Boolean algebras (cf. also Stone space). To describe Priestley's version, let
, [a1]. In the study of distributive lattices, their topological representation plays an important role; this was first established by M.H. Stone [a2], and reformulated in more convenient terms by H.A. Priestley [a3] — both versions generalize the Stone duality for Boolean algebras (cf. also Stone space). To describe Priestley's version, let 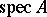 denote the set of prime filters of a distributive lattice
denote the set of prime filters of a distributive lattice  , partially ordered by inclusion and topologized by declaring the sets
, partially ordered by inclusion and topologized by declaring the sets
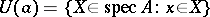 |
and their complements to be subbasic open sets. Then the assignment  is a lattice-isomorphism from
is a lattice-isomorphism from 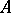 to the set of clopen (i.e. closed and open) subsets of
to the set of clopen (i.e. closed and open) subsets of 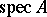 which are upward closed in the partial order. Moreover, the partially ordered spaces which occur as
which are upward closed in the partial order. Moreover, the partially ordered spaces which occur as  for some
for some  are precisely the compact spaces in which, given
are precisely the compact spaces in which, given 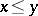 , there exists a clopen upward-closed set containing
, there exists a clopen upward-closed set containing  but not
but not  — such spaces are sometimes called Priestley spaces. Note that a Priestley space
— such spaces are sometimes called Priestley spaces. Note that a Priestley space  is discretely ordered if and only if every prime filter of
is discretely ordered if and only if every prime filter of 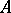 is maximal, if and only if
is maximal, if and only if  is a Boolean algebra. Other important classes of distributive lattices can similarly be characterized by order-theoretic and/or topological properties of their Priestley spaces (see [a4]).
is a Boolean algebra. Other important classes of distributive lattices can similarly be characterized by order-theoretic and/or topological properties of their Priestley spaces (see [a4]).
In addition to the general references [1]–[3] above, [a5] may also be recommended as a general account of distributive lattice theory.
For completely distributive lattices see Completely distributive lattice.
References
| [a1] | G. Birkhoff, "On the combination of subalgebras" Proc. Cambr. Philos. Soc. , 29 (1933) pp. 441–464 |
| [a2] | M.H. Stone, "Topological representation of distributive lattices and Brouwerian logics" Časopis Pešt. Mat. Fys. , 67 (1937) pp. 1–25 |
| [a3] | H.A. Priestley, "Ordered topological spaces and the representation of distributive lattices" Proc. Lond. Math. Soc. (3) , 24 (1972) pp. 507–530 |
| [a4] | H.A. Priestley, "Ordered sets and duality for distributive lattices" , Orders: Description and Roles , Ann. Discrete Math. , 23 , North-Holland (1984) pp. 39–60 |
| [a5] | R. Balbes, P. Dwinger, "Distributive lattices" , Univ. Missouri Press (1974) |
Distributive lattice. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Distributive_lattice&oldid=19143