Difference between revisions of "Distribution of prime numbers"
(→Prime numbers in arithmetic progressions.: link to Dirichlet L-function) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | d0335301.png | ||
| + | $#A+1 = 373 n = 5 | ||
| + | $#C+1 = 373 : ~/encyclopedia/old_files/data/D033/D.0303530 Distribution of prime numbers | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
{{MSC|11N05}} | {{MSC|11N05}} | ||
| − | A branch of number theory studying distribution laws of prime numbers among natural numbers. The central problem is that of finding the best asymptotic, as | + | A branch of number theory studying distribution laws of prime numbers among natural numbers. The central problem is that of finding the best asymptotic, as $ x \rightarrow \infty $, |
| + | expression for the function $ \pi ( x) $, | ||
| + | which is the number of prime numbers not exceeding $ x $, | ||
| + | and for the function $ \pi ( x; d, l) $, | ||
| + | which is the number of prime numbers not exceeding $ x $ | ||
| + | in the arithmetic progression $ dn + l $, | ||
| + | $ 1 \leq l \leq d $, | ||
| + | $ n = 1, 2 \dots $ | ||
| + | for values of $ d $ | ||
| + | increasing along with $ x $. | ||
| − | The fundamental theorem of arithmetic: Any natural number | + | The fundamental theorem of arithmetic: Any natural number $ n > 1 $ |
| + | is either a prime number or a unique (up to permutation of factors) product | ||
| − | + | $$ | |
| + | n = \ | ||
| + | p _ {1} ^ {n _ {1} } \dots | ||
| + | p _ {k} ^ {n _ {k} } | ||
| + | $$ | ||
| − | (the so-called canonical representation of | + | (the so-called canonical representation of $ n $), |
| + | where $ p _ {1} \dots p _ {k} $ | ||
| + | are different prime numbers and $ n _ {1} \dots n _ {k} $ | ||
| + | are natural numbers. Thus, the prime numbers form a multiplicative basis for the set of natural numbers. This, though, says nothing about the value of $ \pi ( x) $. | ||
| − | A method used for finding the prime numbers between 1 and | + | A method used for finding the prime numbers between 1 and $ x $ |
| + | is that of the sieve of Eratosthenes, known since the 3rd century B.C. (cf. [[Eratosthenes, sieve of|Eratosthenes, sieve of]]). The sieve of Eratosthenes is the simplest procedure for obtaining the sequence of prime numbers. But the analytic formula of the sieve, | ||
| − | + | $$ | |
| + | \pi ( x) - | ||
| + | \pi ( \sqrt x ) + 1 = \ | ||
| + | \sum _ { d } | ||
| + | (- 1) ^ {\nu ( d) } | ||
| + | \left [ | ||
| + | { | ||
| + | \frac{x}{d} | ||
| + | } | ||
| + | \right ] , | ||
| + | $$ | ||
| − | where | + | where $ d $ |
| + | takes the values of the divisors of the product of all prime numbers $ \leq \sqrt x $; | ||
| + | $ \nu ( d) $ | ||
| + | is the number of prime divisors of $ d $ | ||
| + | and $ [ u] $ | ||
| + | is the integer part of $ u $, | ||
| + | is not very well suited for studying $ \pi ( x) $ | ||
| + | as $ x \rightarrow \infty $. | ||
| − | The examination of the sequence of prime numbers between 1 and | + | The examination of the sequence of prime numbers between 1 and $ x $: |
| − | + | $$ \tag{1 } | |
| + | 2, 3, 5, 7, 11, 13 \dots p, | ||
| + | $$ | ||
| − | shows that they get ever sparser on the average as | + | shows that they get ever sparser on the average as $ x $ |
| + | increases. There are arbitrarily long segments of the natural series containing no prime number. For instance, the $ n - 1 $ | ||
| + | numbers of the form $ n! + 2 \dots n! + n $ | ||
| + | are all composite for any $ n \geq 2 $. | ||
| + | At the same time, prime numbers that differ by 2, like 8004119 and 8004121, are encountered in (1) ([[Twins|twins]]). The behaviour of $ \pi ( x) $ | ||
| + | as $ x \rightarrow \infty $ | ||
| + | is one of the most difficult and inspiring problems of number theory. | ||
| − | The first result about | + | The first result about $ \pi ( x) $ |
| + | is Euclid's theorem: $ \pi ( x) \rightarrow \infty $ | ||
| + | as $ x \rightarrow \infty $. | ||
| + | L. Euler (1737, 1749, see [[#References|[1]]]) introduced the function | ||
| − | + | $$ \tag{2 } | |
| + | \zeta ( s) = \ | ||
| + | \sum _ {n = 1 } ^ \infty | ||
| + | n ^ {-} s | ||
| + | $$ | ||
and showed that | and showed that | ||
| − | + | $$ \tag{3 } | |
| + | \zeta ( s) = \ | ||
| + | \prod _ { p } | ||
| + | \left ( 1 - | ||
| + | { | ||
| + | \frac{1}{p ^ {s} } | ||
| + | } | ||
| + | \right ) ^ {-} 1 | ||
| + | $$ | ||
| − | for | + | for $ s > 1 $. |
| + | Here the series extends over all natural numbers, and the product over all prime numbers. The identity (3) and its generalizations play a fundamental role in the theory of the distribution of prime numbers. Based on the identity, Euler proved that the series $ \sum 1/p $ | ||
| + | and the product $ \prod ( 1 - 1/p) ^ {-} 1 $ | ||
| + | diverge over the sequence of prime numbers. This is another proof that the set of prime numbers is infinite. Moreover, Euler proved that | ||
| − | + | $$ | |
| + | \pi ( x) > \mathop{\rm log} { | ||
| + | \frac{x}{e} | ||
| + | } , | ||
| + | $$ | ||
which shows that there are "many" prime numbers, although almost-all natural numbers are composite in the sense that | which shows that there are "many" prime numbers, although almost-all natural numbers are composite in the sense that | ||
| − | + | $$ | |
| + | { | ||
| + | \frac{\pi ( x) }{x} | ||
| + | } \rightarrow 0 \ \ | ||
| + | \textrm{ as } x \rightarrow \infty . | ||
| + | $$ | ||
A significant success was subsequently obtained by P.L. Chebyshev (1851–1852, see [[#References|[2]]]). He proved that | A significant success was subsequently obtained by P.L. Chebyshev (1851–1852, see [[#References|[2]]]). He proved that | ||
| − | 1) for any | + | 1) for any $ m, M > 0 $ |
| + | there are sequences $ x, y \rightarrow \infty $ | ||
| + | such that | ||
| − | < | + | $$ |
| + | \pi ( x) - \mathop{\rm li} x < \ | ||
| + | Mx \mathop{\rm log} ^ {-} m x, | ||
| + | $$ | ||
| − | + | $$ | |
| + | \pi ( y) - \mathop{\rm li} y > - My \mathop{\rm log} ^ {-} m y; | ||
| + | $$ | ||
| − | 2) if the quotient | + | 2) if the quotient $ ( \pi ( x) \mathop{\rm log} x)/x $ |
| + | converges as $ x \rightarrow \infty $, | ||
| + | then the limit is equal to 1. | ||
This solved for the first time the question of the existence of a simple function | This solved for the first time the question of the existence of a simple function | ||
| − | + | $$ | |
| + | \mathop{\rm li} x \equiv \ | ||
| + | \int\limits _ { 2 } ^ { x } | ||
| − | + | \frac{du }{ \mathop{\rm log} u } | |
| + | = \ | ||
| + | { | ||
| + | \frac{x}{ \mathop{\rm log} x } | ||
| + | } + \dots + | ||
| − | + | \frac{( r - 1)! | |
| + | x }{ \mathop{\rm log} ^ {r} x } | ||
| + | + | ||
| + | O \left ( | ||
| + | { | ||
| + | \frac{x}{ \mathop{\rm log} ^ {r + 1 } x } | ||
| + | } | ||
| + | \right ) , | ||
| + | $$ | ||
| − | + | which approximates $ \pi ( x) $ | |
| + | optimally. | ||
| − | + | Then Chebyshev established the true order of growth of $ \pi ( x) $, | |
| + | that is, the existence of constants $ a > 0 $ | ||
| + | and $ A > 0 $ | ||
| + | such that | ||
| − | < | + | $$ \tag{4 } |
| + | a { | ||
| + | \frac{x}{ \mathop{\rm log} x } | ||
| + | } < \ | ||
| + | \pi ( x) < \ | ||
| + | A { | ||
| + | \frac{x}{ \mathop{\rm log} x } | ||
| + | } ; | ||
| + | $$ | ||
| − | + | notably, $ a = 0.92 \dots $, | |
| + | $ A = 1.05 \dots $ | ||
| + | for $ x \geq x _ {0} $. | ||
| + | He also proved that for any $ n \geq 2 $ | ||
| + | the interval $ ( n, 2n) $ | ||
| + | contains at least one prime number (Bertrand's postulate). The proof of (4) is based on Chebyshev's identity | ||
| − | + | $$ \tag{5 } | |
| + | F ( x) \equiv \ | ||
| + | \mathop{\rm log} [ x]! = \ | ||
| + | \sum _ {n \leq x } | ||
| + | \psi \left ( | ||
| + | { | ||
| + | \frac{x}{n} | ||
| + | } | ||
| + | \right ) , | ||
| + | $$ | ||
| − | + | where the function $ \psi $, | |
| + | introduced by Chebyshev, is defined by the sum | ||
| − | + | $$ | |
| + | \psi ( x) = \ | ||
| + | \sum _ {p ^ {m} \leq x } | ||
| + | \mathop{\rm log} p = \ | ||
| + | \sum _ {n < x } | ||
| + | \Delta ( n), | ||
| + | $$ | ||
| + | |||
| + | taken over all powers $ p ^ {m} $, | ||
| + | $ m \in \mathbf N $, | ||
| + | of prime numbers $ p $. | ||
| + | Namely, if $ x \geq 30 $, | ||
| + | the following combination of $ \mathop{\rm log} [ u]! $: | ||
| + | |||
| + | $$ | ||
| + | F ^ { * } ( x) = \ | ||
| + | F ( x) + F | ||
| + | \left ( | ||
| + | { | ||
| + | \frac{x}{30} | ||
| + | } | ||
| + | \right ) - F | ||
| + | \left ( | ||
| + | { | ||
| + | \frac{x}{2} | ||
| + | } | ||
| + | \right ) - F | ||
| + | \left ( | ||
| + | { | ||
| + | \frac{x}{3} | ||
| + | } | ||
| + | \right ) - F | ||
| + | \left ( | ||
| + | { | ||
| + | \frac{x}{6} | ||
| + | } | ||
| + | \right ) , | ||
| + | $$ | ||
owing to (5), gives the identity | owing to (5), gives the identity | ||
| − | + | $$ | |
| + | F ^ { * } ( x) = \ | ||
| + | \psi ( x) - \psi | ||
| + | \left ( | ||
| + | { | ||
| + | \frac{x}{6} | ||
| + | } | ||
| + | \right ) + \psi | ||
| + | \left ( | ||
| + | { | ||
| + | \frac{x}{7} | ||
| + | } | ||
| + | \right ) - \psi | ||
| + | \left ( | ||
| + | { | ||
| + | \frac{x}{10} | ||
| + | } | ||
| + | \right ) + \dots , | ||
| + | $$ | ||
which implies | which implies | ||
| − | < | + | $$ |
| + | \psi ( x) - \psi | ||
| + | \left ( | ||
| + | { | ||
| + | \frac{x}{6} | ||
| + | } | ||
| + | \right ) < \ | ||
| + | F ^ {*} ( x) < \ | ||
| + | \psi ( x). | ||
| + | $$ | ||
| − | By virtue of Stirling's asymptotic formula for | + | By virtue of Stirling's asymptotic formula for $ n! $ |
| + | this implies an analogue of (4) for $ \psi ( x) $ | ||
| + | from which (4) is obtained by partial summation. Chebyshev's function $ \psi ( x) $ | ||
| + | proved to be more convenient for studying the distribution of prime numbers than $ \pi ( x) $, | ||
| + | since the best approximation for it is the very argument $ x $. | ||
| + | Therefore $ \psi ( x) $ | ||
| + | is usually considered first and then the corresponding result for $ \pi ( x) $ | ||
| + | is obtained by partial summation. | ||
==Riemann's principle.== | ==Riemann's principle.== | ||
| − | In 1859–1860 B. Riemann [[#References|[3]]] considered the function | + | In 1859–1860 B. Riemann [[#References|[3]]] considered the function $ \zeta ( s) $, |
| + | introduced by Euler for $ s > 1 $, | ||
| + | as a function of a complex variable $ s = \sigma + it $, | ||
| + | where $ \sigma $ | ||
| + | and $ t $ | ||
| + | are real variables, defined by (2) for $ \sigma > 1 $( | ||
| + | see [[Zeta-function|Zeta-function]]) and found that this function is extremely important in the theory of the distribution of prime numbers. In particular, he found an expression for the difference $ \pi ( x) - \mathop{\rm li} x $ | ||
| + | in terms of $ x $ | ||
| + | and those zeros of $ \zeta ( s) $ | ||
| + | which belong to the strip $ 0 \leq \sigma \leq 1 $; | ||
| + | they are called the non-trivial zeros of $ \zeta ( s) $. | ||
| − | Instead of Riemann's formula, its simpler finite analogue for | + | Instead of Riemann's formula, its simpler finite analogue for $ \psi ( x) $, |
| + | proved (along with Riemann's formula) by H. (von) Mangoldt in 1895, is often used. Namely, for $ x > 1 $: | ||
| − | + | $$ \tag{6 } | |
| + | \psi ( x) = x - | ||
| + | \sum _ {| \gamma | \leq T } | ||
| + | { | ||
| + | \frac{x ^ \rho } \rho | ||
| + | } + O | ||
| + | \left ( | ||
| + | { | ||
| + | \frac{x}{T} | ||
| + | } \ | ||
| + | \mathop{\rm log} ^ {2} xT + | ||
| + | \mathop{\rm log} 2x | ||
| + | \right ) , | ||
| + | $$ | ||
| − | where | + | where $ \rho = \rho + i \gamma $ |
| + | runs through the non-trivial zeros of $ \zeta ( s) $ | ||
| + | and $ T \geq 2 $ | ||
| + | is arbitrary. | ||
Since | Since | ||
| − | + | $$ | |
| + | \sum _ {| \gamma | \leq T } | ||
| + | { | ||
| + | \frac{1} \gamma | ||
| + | } \ll \ | ||
| + | \mathop{\rm log} ^ {2} T, | ||
| + | $$ | ||
| + | |||
| + | (6) shows that the difference $ \psi ( x) - x $ | ||
| + | is primarily defined by $ \beta $( | ||
| + | the real part of the right-most zeros $ \rho $). | ||
| + | In particular, the following asymptotic expressions are valid for $ \psi ( x) $ | ||
| + | and $ \pi ( x) $: | ||
| − | ( | + | $$ |
| + | \psi ( x) = \ | ||
| + | x + O | ||
| + | ( x ^ \theta \ | ||
| + | \mathop{\rm log} ^ {2} x), | ||
| + | $$ | ||
| − | + | $$ | |
| + | \pi ( x) = \mathop{\rm li} x + O ( x ^ \theta \mathop{\rm log} x), | ||
| + | $$ | ||
| − | + | provided that $ \zeta ( x) \neq 0 $ | |
| + | to the right of a vertical $ \sigma = \theta $, | ||
| + | $ 1/2 \leq \theta < 1 $. | ||
| + | Conversely, it follows from these relations that $ \zeta ( s) \neq 0 $ | ||
| + | if $ \sigma \geq \theta $. | ||
| + | If the Riemann hypothesis holds, that is, if all non-trivial zeros of $ \zeta ( s) $ | ||
| + | lie on the line $ \sigma = 1/2 $, | ||
| + | then the asymptotic distribution law for prime numbers must have the form | ||
| − | + | $$ | |
| + | \psi ( x) = \ | ||
| + | x + O ( \sqrt x \ | ||
| + | \mathop{\rm log} ^ {2} x), | ||
| + | $$ | ||
| − | + | $$ | |
| + | \pi ( x) = \mathop{\rm li} x + O ( \sqrt x \mathop{\rm log} x), | ||
| + | $$ | ||
| − | + | and these relations cannot be substantially strengthened. The latter means that there are sequences $ x, y \rightarrow \infty $ | |
| + | such that | ||
| − | + | $$ | |
| + | \pi ( x) - \mathop{\rm li} x < \ | ||
| + | - \sqrt x | ||
| − | + | \frac{ \mathop{\rm log} \mathop{\rm log} \mathop{\rm log} x }{ \mathop{\rm log} \mathop{\rm log} x } | |
| + | , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \pi ( y) - \mathop{\rm li} y > + y | ||
| + | \frac{ \mathop{\rm log} \mathop{\rm log} \mathop{\rm log} y }{ \mathop{\rm log} \mathop{\rm log} y } | ||
| + | . | ||
| + | $$ | ||
| − | Thus, by Riemann's principle, the problem about the asymptotic expressions for | + | Thus, by Riemann's principle, the problem about the asymptotic expressions for $ \psi ( x) $ |
| + | and $ \pi ( x) $ | ||
| + | reduces to that about bounds for the real part of the non-trivial zeros of $ \zeta ( x) $. | ||
| + | Till now (1983), however, no constant $ \theta $, | ||
| + | $ 1/2 \leq \theta < 1 $, | ||
| + | has been found with the condition $ \beta < \theta $. | ||
| + | The desired bound for $ \beta $ | ||
| + | turns out to be connected with the imaginary part $ \gamma $ | ||
| + | of zeros $ \rho $ | ||
| + | in such a way that the line $ \sigma = 1 $ | ||
| + | is its asymptote. | ||
==The methods of Hadamard and de la Vallée-Poussin.== | ==The methods of Hadamard and de la Vallée-Poussin.== | ||
In its simplest form | In its simplest form | ||
| − | + | $$ | |
| + | \lim\limits _ {x \rightarrow \infty } \ | ||
| + | { | ||
| + | \frac{\pi ( x) \mathop{\rm log} x }{x} | ||
| + | } = \ | ||
| + | \lim\limits _ {x \rightarrow \infty } \ | ||
| + | { | ||
| + | \frac{\psi ( x) }{x} | ||
| + | } = 1 | ||
| + | $$ | ||
| − | the asymptotic distribution law for prime numbers was independently obtained in 1896 by J. Hadamard and Ch.J. de la Vallée-Poussin, who proved that | + | the asymptotic distribution law for prime numbers was independently obtained in 1896 by J. Hadamard and Ch.J. de la Vallée-Poussin, who proved that $ \zeta ( 1 + it) \neq 0 $, |
| + | that is, there is no zero of $ \zeta ( s) $ | ||
| + | on the line $ \sigma = 1 $. | ||
| + | In 1899 de la Vallée-Poussin showed that $ \zeta ( \sigma + it) \neq 0 $ | ||
| + | in the domain $ \sigma \geq 1 - c/ \mathop{\rm log} ( | t | + 2) $. | ||
| + | It was thereby proved that | ||
| − | + | $$ | |
| + | \psi ( x) = x + O | ||
| + | ( x \mathop{\rm exp} (- a | ||
| + | \sqrt { \mathop{\rm log} x } )), | ||
| + | $$ | ||
| − | + | $$ | |
| + | \pi ( x) = \mathop{\rm li} x + O ( x \mathop{\rm exp} (- b \sqrt { \mathop{\rm log} x } )) , | ||
| + | $$ | ||
| − | where | + | where $ a, b > 0 $ |
| + | are constants. | ||
| − | Further extensions of the region containing no zeros of | + | Further extensions of the region containing no zeros of $ \zeta ( s) $ |
| + | were also obtained (see [[#References|[4]]]–[[#References|[12]]]). | ||
==The method of Weyl–Littlewood.== | ==The method of Weyl–Littlewood.== | ||
| − | There is a certain connection between the growth of the modulus of | + | There is a certain connection between the growth of the modulus of $ \zeta ( s) $ |
| + | and its zeros near the line $ \sigma = 1 $. | ||
| + | In particular, if $ | \zeta ( s) | \ll \mathop{\rm exp} \phi ( t) $ | ||
| + | for $ 1 - \theta ( t) \leq \sigma \leq 2 $, | ||
| + | where $ \phi ( t) $ | ||
| + | and $ 1/ \theta ( t) $ | ||
| + | are positive non-decreasing functions of $ t \geq 0 $ | ||
| + | such that $ \theta ( t) \leq 1 $, | ||
| + | $ \phi ( t) \rightarrow \infty $ | ||
| + | as $ t \rightarrow \infty $ | ||
| + | and $ \phi ( t)/ \theta ( t) \ll \mathop{\rm exp} \phi ( t) $, | ||
| + | then there is a constant $ A $ | ||
| + | such that $ \zeta ( s) \neq 0 $ | ||
| + | in the region | ||
| + | |||
| + | $$ | ||
| + | \sigma \geq 1 - | ||
| − | + | \frac{A \theta ( 2t + 1) }{\phi ( 2t + 1) } | |
| + | . | ||
| + | $$ | ||
| − | The estimate for | + | The estimate for $ \zeta ( s) $ |
| + | is here obtained with the help of the partial sums of the series (2). This reduces the problem to the estimation of trigonometric sums of the form | ||
| − | < | + | $$ |
| + | \sum _ {v < n \leq u } | ||
| + | \mathop{\rm exp} ( it \mathop{\rm log} n). | ||
| + | $$ | ||
| − | By estimating such sums by the [[Weyl method|Weyl method]], J.E. Littlewood showed in 1921 that | + | By estimating such sums by the [[Weyl method|Weyl method]], J.E. Littlewood showed in 1921 that $ | \zeta ( s) | \ll \mathop{\rm log} ^ {5} t $ |
| + | if $ t > A $ | ||
| + | and $ \sigma \geq 1 - \mathop{\rm log} ^ {2} \mathop{\rm log} t/ \mathop{\rm log} t $, | ||
| + | so that $ \zeta ( s) \neq 0 $ | ||
| + | in the region | ||
| − | + | $$ | |
| + | \sigma \geq 1 - | ||
| + | |||
| + | \frac{A \mathop{\rm log} \mathop{\rm log} t }{ \mathop{\rm log} t } | ||
| + | . | ||
| + | $$ | ||
It follows that | It follows that | ||
| − | + | $$ | |
| + | \pi ( x) = \ | ||
| + | \mathop{\rm li} x + O | ||
| + | ( x \mathop{\rm exp} (- a | ||
| + | \sqrt { \mathop{\rm log} x \mathop{\rm log} \mathop{\rm log} x } )). | ||
| + | $$ | ||
==The method of Vinogradov.== | ==The method of Vinogradov.== | ||
| − | A further advance in the estimation of | + | A further advance in the estimation of $ \pi ( x) $ |
| + | and $ \psi ( x) $ | ||
| + | is connected with development by I.M. Vinogradov of a new and substantially more powerful method for the estimation of trigonometric sums (see [[Vinogradov method|Vinogradov method]]). Using this method, he showed in 1938 that $ \zeta ( s) \neq 0 $ | ||
| + | if | ||
| − | + | $$ | |
| + | \sigma \geq 1 - { | ||
| + | \frac{c}{ \mathop{\rm log} ^ {3/4} ( | t | + 2) \ | ||
| + | \mathop{\rm log} ^ {3/4} \mathop{\rm log} ( | t | + 2) } | ||
| + | } , | ||
| + | $$ | ||
and consequently that | and consequently that | ||
| − | + | $$ | |
| + | \pi ( x) = \ | ||
| + | \mathop{\rm li} x + O | ||
| + | ( x \mathop{\rm exp} (- a \ | ||
| + | \mathop{\rm log} ^ {4/7} x \ | ||
| + | \mathop{\rm log} ^ {-} 3/7 \ | ||
| + | \mathop{\rm log} x)). | ||
| + | $$ | ||
| − | In 1958 Vinogradov and others (see [[#References|[6]]]–[[#References|[11]]]) showed that | + | In 1958 Vinogradov and others (see [[#References|[6]]]–[[#References|[11]]]) showed that $ \zeta ( s) \neq 0 $ |
| + | if | ||
| − | + | $$ | |
| + | \sigma \geq 1 - { | ||
| + | \frac{c}{ \mathop{\rm log} ^ {2/3} | ||
| + | ( | t | + 2) \ | ||
| + | \mathop{\rm log} ^ {1/3} \mathop{\rm log} | ||
| + | ( | t | + 2) } | ||
| + | } . | ||
| + | $$ | ||
| − | So far (1983) this is the best result concerning bounds on the non-trivial zeros of | + | So far (1983) this is the best result concerning bounds on the non-trivial zeros of $ \zeta ( s) $, |
| + | to which the following best result on the distribution of prime numbers corresponds: | ||
| − | + | $$ | |
| + | \pi ( x) = \ | ||
| + | \mathop{\rm li} x + | ||
| + | O ( x \mathop{\rm exp} | ||
| + | (- a \mathop{\rm log} ^ {3/5} \ | ||
| + | x \mathop{\rm log} ^ {-} 1/5 \ | ||
| + | \mathop{\rm log} x)), | ||
| + | $$ | ||
| − | + | $$ | |
| + | \psi ( x) = x + O ( x \mathop{\rm exp} (- b \mathop{\rm log} ^ {3/5} x \mathop{\rm log} ^ {-} 1/5 \mathop{\rm log} x)). | ||
| + | $$ | ||
| − | The asymptotics for the | + | The asymptotics for the $ n $- |
| + | th prime number, $ p _ {n} \sim n \mathop{\rm log} n $, | ||
| + | follow from the asymptotics of $ \pi ( x) $. | ||
| + | It was also shown (see [[#References|[21]]]) that $ p _ {n} > n \mathop{\rm log} n $ | ||
| + | for all $ n \geq 1 $ | ||
| + | and that for $ 17 \leq x \leq e ^ {100} $, | ||
| + | $ x \geq e ^ {200} $, | ||
| − | < | + | $$ |
| + | { | ||
| + | \frac{x}{ \mathop{\rm log} x } | ||
| + | } < \ | ||
| + | \pi ( x) < \ | ||
| + | { | ||
| + | \frac{x}{ \mathop{\rm log} x - 2 } | ||
| + | } ; | ||
| + | $$ | ||
| − | and for | + | and for $ x \geq 55 $, |
| − | < | + | $$ |
| + | { | ||
| + | \frac{x}{ \mathop{\rm log} x + 2 } | ||
| + | } < \ | ||
| + | \pi ( x) < \ | ||
| + | { | ||
| + | \frac{x}{ \mathop{\rm log} x - 4 } | ||
| + | } . | ||
| + | $$ | ||
==Elementary methods.== | ==Elementary methods.== | ||
This is the name for methods for studying the asymptotic distribution of prime numbers that are not based on Riemann's principle (zeros of the zeta-function) and, in general, on any principles from the theory of functions of a complex variable whatsoever. Such a method was first discovered by A. Selberg [[#References|[16]]] and P. Erdös [[#References|[17]]]. It is based on the elementary formula of Selberg | This is the name for methods for studying the asymptotic distribution of prime numbers that are not based on Riemann's principle (zeros of the zeta-function) and, in general, on any principles from the theory of functions of a complex variable whatsoever. Such a method was first discovered by A. Selberg [[#References|[16]]] and P. Erdös [[#References|[17]]]. It is based on the elementary formula of Selberg | ||
| − | + | $$ \tag{7 } | |
| + | \psi ( x) \mathop{\rm log} x + | ||
| + | \sum _ {n \leq x } | ||
| + | \psi \left ( | ||
| + | { | ||
| + | \frac{x}{n} | ||
| + | } | ||
| + | \right ) | ||
| + | \Lambda ( n) = \ | ||
| + | 2x \mathop{\rm log} x + O ( x). | ||
| + | $$ | ||
| − | A further problem consists in obtaining asymptotics for | + | A further problem consists in obtaining asymptotics for $ \psi ( x) $ |
| + | from the averaged asymptotics for $ \psi ( u) $ | ||
| + | given by (7). It may be done in different ways but all of them employ the fact that $ \psi ( x) $ | ||
| + | slowly oscillates. In 1962 E. Bombieri and E. Wirsing proved that | ||
| − | + | $$ | |
| + | \psi ( x) = \ | ||
| + | x + O | ||
| + | ( x \mathop{\rm log} ^ {-} A x) | ||
| + | $$ | ||
| − | for any fixed | + | for any fixed $ A > 0 $. |
| + | In 1970, H.G. Diamond and J. Steinig [[#References|[19]]] substantially perfected the principles and techniques of estimation by means of an elementary method. They proved that for $ x \geq \mathop{\rm exp} \mathop{\rm exp} 100 $, | ||
| − | < | + | $$ |
| + | | \psi ( x) - x | < \ | ||
| + | x \mathop{\rm exp} (- \mathop{\rm log} ^ {1/7} \ | ||
| + | x \mathop{\rm log} ^ {-} 2 \mathop{\rm log} x). | ||
| + | $$ | ||
| − | Finally, in 1973 A.F. Lavrik and A.Sh. Sobirov [[#References|[20]]] showed that an elementary method enables one to prove the following theorem: For | + | Finally, in 1973 A.F. Lavrik and A.Sh. Sobirov [[#References|[20]]] showed that an elementary method enables one to prove the following theorem: For $ x \geq \mathop{\rm exp} \mathop{\rm exp} 10 ^ {3} $, |
| − | < | + | $$ |
| + | | \psi ( x) - x | < \ | ||
| + | x \mathop{\rm exp} (- \mathop{\rm log} ^ {1/6} \ | ||
| + | x \mathop{\rm log} ^ {-} 3 \mathop{\rm log} x). | ||
| + | $$ | ||
This result is so far the best achievement of the elementary method as regards the distribution of prime numbers. Although it is somewhat weaker than the result obtained by the analytic method, in principle they are close. | This result is so far the best achievement of the elementary method as regards the distribution of prime numbers. Although it is somewhat weaker than the result obtained by the analytic method, in principle they are close. | ||
==The difference between prime numbers.== | ==The difference between prime numbers.== | ||
| − | There are many questions in the distribution of prime numbers that are concerned with differences between prime numbers. Standing out among them are questions about the behaviour of the difference | + | There are many questions in the distribution of prime numbers that are concerned with differences between prime numbers. Standing out among them are questions about the behaviour of the difference $ d _ {n} = p _ {n + 1 } - p _ {n} $ |
| + | between adjacent prime numbers; the problem on the number of prime twins or, more generally, pairs of prime numbers that differ by $ 2k $ | ||
| + | or, in the most general form, the problem about the number of systems $ p, p + u _ {1} \dots p + u _ {m} $ | ||
| + | of $ m + 1 $ | ||
| + | prime numbers within the segment $ [ 1, x] $. | ||
| − | Using Riemann's hypothesis it was proved that | + | Using Riemann's hypothesis it was proved that $ d _ {n} \ll \sqrt {p _ {n} } \mathop{\rm log} p _ {n} $, |
| + | and heuristic considerations suggest that probably $ d _ {n} \ll \mathop{\rm log} ^ {2} p _ {n} $. | ||
| + | By 1983, the best estimate $ d _ {n} \ll p _ {n} ^ \delta $, | ||
| + | where $ \delta = ( 7/12) + \epsilon $, | ||
| + | $ \epsilon > 0 $, | ||
| + | was obtained by M.N. Huxley (1973) using the method of the large sieve. As for pairs of prime numbers whose difference is equal to 2 (twins) or to $ 2k $, | ||
| + | $ k = 1, 2 \dots $ | ||
| + | it is still (1983) unknown whether the number of such pairs is finite or not. Let $ \pi _ {k} ( x) $ | ||
| + | be the number of prime numbers that do not exceed $ x $ | ||
| + | and differ by $ 2k $. | ||
| + | In 1919 V. Brun found a sieve method (see [[Brun sieve|Brun sieve]]) that permitted one to obtain the expected upper bound for $ \pi _ {k} ( x) $: | ||
| − | + | $$ | |
| + | \pi _ {k} ( x) \ll \ | ||
| + | { | ||
| + | \frac{x}{ \mathop{\rm log} ^ {2} x } | ||
| + | } | ||
| + | \prod _ { p\mid } k | ||
| + | \left ( | ||
| + | 1 - { | ||
| + | \frac{1}{p} | ||
| + | } | ||
| + | \right ) ^ {-} 1 . | ||
| + | $$ | ||
| − | In addition to that, it was shown by the [[Circle method|circle method]] (see [[#References|[13]]]) with the help of Vinogradov's estimates for trigonometric sums with prime numbers (see [[Vinogradov method|Vinogradov method]]) that for any fixed | + | In addition to that, it was shown by the [[Circle method|circle method]] (see [[#References|[13]]]) with the help of Vinogradov's estimates for trigonometric sums with prime numbers (see [[Vinogradov method|Vinogradov method]]) that for any fixed $ A > 1 $, |
| + | $ M > 0 $, | ||
| − | + | $$ | |
| + | \sum _ {1 \leq 2h \leq x \mathop{\rm log} ^ {-} A x } | ||
| + | \left [ | ||
| + | \pi _ {k} ( x) - f ( x) | ||
| + | \prod _ {\begin{array}{c} | ||
| + | p\mid k \\ | ||
| + | p > 2 | ||
| + | \end{array} | ||
| + | } | ||
| + | |||
| + | \frac{p - 1 }{p - 2 } | ||
| + | |||
| + | \right ] ^ {2} \ll \ | ||
| + | x ^ {3} \mathop{\rm log} ^ {- A - M } x, | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | f ( x) = 2 | ||
| + | \prod _ {p > 2 } | ||
| + | \left ( 1 - | ||
| + | { | ||
| + | \frac{1}{( p - 1) ^ {2} } | ||
| + | } | ||
| + | \right ) | ||
| + | \int\limits _ { 2 } ^ { x } | ||
| − | + | \frac{du }{ \mathop{\rm log} ^ {2} u } | |
| + | . | ||
| + | $$ | ||
| − | + | This implies, in particular, that for $ X = x \mathop{\rm log} ^ {-} A x $ | |
| + | the following asymptotic expression for $ \pi _ {k} ( x) $ | ||
| + | holds for all $ 1 \leq k \leq X $ | ||
| + | except for at most $ X \mathop{\rm log} ^ {-} M x $ | ||
| + | values of $ k $ | ||
| + | in the range $ 1 \leq k \leq X $: | ||
| − | Similar results are obtained for sets of prime numbers | + | $$ |
| + | \pi _ {k} ( x) \sim 2 | ||
| + | \prod _ {p > 2 } | ||
| + | \left ( 1 - | ||
| + | { | ||
| + | \frac{1}{( p - 1) ^ {2} } | ||
| + | } | ||
| + | \right ) | ||
| + | { | ||
| + | \frac{x}{ \mathop{\rm log} ^ {2} x } | ||
| + | } | ||
| + | \prod _ {\begin{array}{c} | ||
| + | p\mid k \\ | ||
| + | p > 2 | ||
| + | \end{array} | ||
| + | } | ||
| + | |||
| + | \frac{p - 1 }{p - 2 } | ||
| + | . | ||
| + | $$ | ||
| + | |||
| + | Similar results are obtained for sets of prime numbers $ p, p + u _ {1} \dots p + u _ {m} $ | ||
| + | for all $ m \geq 1 $. | ||
==Prime numbers in arithmetic progressions.== | ==Prime numbers in arithmetic progressions.== | ||
| − | The first method (of Euclid) for proving the infinitude of prime numbers can also be applied to certain arithmetic progressions. But the proof by this method that every arithmetic progression | + | The first method (of Euclid) for proving the infinitude of prime numbers can also be applied to certain arithmetic progressions. But the proof by this method that every arithmetic progression $ dn + l $, |
| + | where the first number $ l $ | ||
| + | and the difference $ d $ | ||
| + | are relatively prime, contains infinitely many prime numbers has not yet (1983) been given. The problem was solved by another method by P. Dirichlet (1837–1840), who extended an idea of Euler in showing that $ \sum 1/p ^ {s} \rightarrow \infty $ | ||
| + | as $ s \rightarrow 1 + 0 $ | ||
| + | for prime numbers $ p \equiv l ( \mathop{\rm mod} d) $. | ||
| + | To do this he introduced certain arithmetical functions — characters $ \chi = \chi ( n, d) $( | ||
| + | see [[Dirichlet character|Dirichlet character]]) and functions $ L ( s, \chi ) $( | ||
| + | see [[Dirichlet L-function|Dirichlet $ L $- | ||
| + | function]]), which, like $ \zeta ( s) $ | ||
| + | for $ \pi ( x) $ | ||
| + | and $ \psi ( x) $, | ||
| + | serve as a basic means of studying $ \pi ( x; d, l) $ | ||
| + | and its analogue | ||
| − | + | $$ | |
| + | \psi ( x; d, l) = \ | ||
| + | \sum _ {\begin{array}{c} | ||
| + | n \leq x, | ||
| + | \\ | ||
| + | n \equiv l ( \mathop{\rm mod} d) | ||
| + | \end{array} | ||
| + | } | ||
| + | \Lambda ( n). | ||
| + | $$ | ||
| − | For a fixed value of | + | For a fixed value of $ d $, |
| + | $ 1 \leq l \leq d $, | ||
| + | $ ( l, d) = 1 $, | ||
| + | the majority of results indicated above for $ \pi ( x) $ | ||
| + | and $ \psi ( x) $ | ||
| + | carry over to $ \pi ( x; d, l) $ | ||
| + | and $ \psi ( x; d, l) $. | ||
| + | However, of special interest here are the results for values of $ d $ | ||
| + | that increase with $ x $, | ||
| + | as these are important in additive number theory and elsewhere. In this case, other significant difficulties arise, connected mostly with estimating $ d $, | ||
| + | the largest real zero of $ L ( s, \chi ) $ | ||
| + | modulo $ d $. | ||
| + | It can be proved using the [[Page theorem|Page theorem]] that for $ 1 \leq d \leq ( \mathop{\rm log} x) ^ {2 - \epsilon } $, | ||
| + | $ 0 < \epsilon < 1/2 $, | ||
| − | + | $$ | |
| + | \psi ( x; d, l) = \ | ||
| + | { | ||
| + | \frac{x}{\phi ( d) } | ||
| + | } + | ||
| + | O ( x \mathop{\rm exp} (- a \ | ||
| + | \mathop{\rm log} ^ {\epsilon /3 } x)), | ||
| + | $$ | ||
| − | and as a result of C.L. Siegel's bound (1935), for any fixed | + | and as a result of C.L. Siegel's bound (1935), for any fixed $ A > 1 $, |
| + | for $ 1 \leq d \leq \mathop{\rm log} ^ {A} x $, | ||
| − | + | $$ | |
| + | \psi ( x; d, l) = \ | ||
| + | { | ||
| + | \frac{x}{\phi ( d) } | ||
| + | } + | ||
| + | O ( x \mathop{\rm exp} (- c _ {1} \sqrt { \mathop{\rm log} x } )), | ||
| + | $$ | ||
| − | where | + | where $ \phi ( d) $ |
| + | is the Euler $ \phi $- | ||
| + | function, $ a $ | ||
| + | is a positive constant and $ c _ {1} = c _ {1} ( A) $ | ||
| + | is an ineffective constant $ > 0 $, | ||
| + | that is, $ c _ {1} $ | ||
| + | cannot be computed for given $ A $. | ||
| − | If the extended Riemann hypothesis (cf. [[Riemann hypotheses|Riemann hypotheses]]) is true, then for | + | If the extended Riemann hypothesis (cf. [[Riemann hypotheses|Riemann hypotheses]]) is true, then for $ d \leq x $, |
| − | + | $$ | |
| + | \psi ( x; d, l) = \ | ||
| + | { | ||
| + | \frac{x}{\phi ( d) } | ||
| + | } + | ||
| + | O ( \sqrt x \mathop{\rm log} ^ {2} x). | ||
| + | $$ | ||
| − | Thus, up till 1983 it has been proved that the prime numbers are uniformly distributed over all | + | Thus, up till 1983 it has been proved that the prime numbers are uniformly distributed over all $ \phi ( d) $ |
| + | progressions $ 1 \leq l \leq d $, | ||
| + | $ ( l, d) = 1 $, | ||
| + | of difference $ d $ | ||
| + | only for $ d \leq \mathop{\rm log} ^ {A} x $. | ||
| + | As far as segments of progressions $ dn + l \leq x $ | ||
| + | are concerned, for example with $ d = x ^ \epsilon $ | ||
| + | for any $ \epsilon > 0 $, | ||
| + | it does not even follow from the above that such a progression contains at least one prime number. | ||
| − | The sieve method of Brun, like the modification suggested by Selberg in 1947, shows that for all < | + | The sieve method of Brun, like the modification suggested by Selberg in 1947, shows that for all $ 1 \leq d < x $, |
| + | $ 1 \leq l \leq d $, | ||
| + | $ ( l, d) = 1 $, | ||
| + | there is an upper bound | ||
| − | + | $$ | |
| + | \pi ( x; d, l) \ll \ | ||
| − | + | \frac{Cx }{\phi ( d) \mathop{\rm log} { | |
| + | \frac{x}{d} | ||
| + | } } | ||
| + | , | ||
| + | $$ | ||
| − | + | with absolute constant $ C $, | |
| + | but no lower bounds for $ \pi ( x; d, l) $ | ||
| + | are obtainable by these methods. | ||
| − | + | By the Riemann principle for a zero $ \rho = \beta + i \gamma $ | |
| + | of $ L ( s, \chi ) $ | ||
| + | lying in the strip $ 0 \leq \sigma \leq 1 $, | ||
| + | $ \psi ( x; d, l) $ | ||
| + | has the form | ||
| − | + | $$ \tag{8 } | |
| + | \psi ( x; d, l) = \ | ||
| − | + | \frac{\psi ( x) }{\phi ( d) } | |
| + | + | ||
| + | $$ | ||
| − | + | $$ | |
| + | - { | ||
| + | \frac{1}{\phi ( d) } | ||
| + | } \left ( \sum _ \chi {} | ||
| + | \prime \overline \chi \; ( l) \sum _ {| \gamma | \leq T } { | ||
| + | \frac{x ^ \rho } \rho | ||
| + | } + { | ||
| + | \frac{\overline \chi \; ( l) x ^ \alpha } \alpha | ||
| + | } \right ) + R, | ||
| + | $$ | ||
| − | + | where the prime on the $ \sum $ | |
| + | indicates summation over complex $ \chi $ | ||
| + | $ \mathop{\rm mod} d $, | ||
| + | $ \alpha $ | ||
| + | is the real zero of $ L ( s, \chi ) $ | ||
| + | if it exists and is greater than $ 1 - C _ {0} / \mathop{\rm log} d $, | ||
| + | and | ||
| − | + | $$ | |
| + | R \ll xT ^ {-} 1 \ | ||
| + | \mathop{\rm log} ^ {2} dx + | ||
| + | x ^ {1/4} \mathop{\rm log} x, | ||
| + | $$ | ||
| − | + | for any $ T \geq 2 $. | |
| − | + | From (8) one sees that if one disregards the term corresponding to $ \alpha $, | |
| + | the remainder term is determined by the double sum and depends also on the real part of $ \rho $ | ||
| + | and on all the $ L ( x, \chi ) $ | ||
| + | with $ \chi $ | ||
| + | $ \mathop{\rm mod} d $ | ||
| + | having a zero $ \rho $ | ||
| + | with $ \mathop{\rm Re} \rho = \beta $. | ||
| + | If, for $ 0.5 \leq \sigma \leq 1 $, | ||
| + | $ N ( \sigma , T, \chi ) $ | ||
| + | denotes the number of zeros of $ L ( s, \chi ) $ | ||
| + | in the rectangle $ \sigma \leq \mathop{\rm Re} s \leq 1 $, | ||
| + | $ | t | \leq T $, | ||
| + | then the problem of estimating the remainder term for $ \psi ( x; d, l) $ | ||
| + | and its mean value is reduced to the problem of estimating the density of the distribution of the zeros of $ L $- | ||
| + | functions: | ||
| − | + | $$ \tag{9 } | |
| + | \left . | ||
| − | + | \begin{array}{c} | |
| + | N _ {1} \equiv \ | ||
| + | \sum _ {\chi \mathop{\rm mod} d } {} \prime | ||
| + | N ( \sigma , T, \chi ), \\ | ||
| + | N _ {2} \equiv \ | ||
| + | \sum _ {d \leq D } \ | ||
| + | \sum _ {\chi \mathop{\rm mod} d } {} \prime | ||
| + | N ( \sigma , T, \chi ). \\ | ||
| + | \end{array} | ||
| − | + | \right \} | |
| + | $$ | ||
| − | + | Thus, the reduction of various estimates for prime numbers is concerned not so much with the lack of zeros of $ L ( s, \chi ) $ | |
| + | in the critical strip, but with their comparatively rare distribution there. | ||
| − | + | The realization of this idea has been one of the central directions of research on the distribution of prime numbers over the last forty years. A start was made by Yu.V. Linnik with his discovery in 1941 of the method of the [[Large sieve|large sieve]] (see [[#References|[22]]], and also [[#References|[14]]], [[#References|[24]]]). Especially important are the theorems on the least prime number in an arithmetic progression, the behaviour of $ \pi ( x; d, l) $ | |
| + | and $ \psi ( x; d, l) $ | ||
| + | on the average for $ d \leq D $, | ||
| + | and on the double averaging of these functions over $ 1 \leq l \leq d $, | ||
| + | $ ( l, d) = 1 $, | ||
| + | and over $ d \leq D $. | ||
| − | + | Namely, in 1944 Linnik [[#References|[23]]] showed that as $ d \rightarrow \infty $ | |
| + | the sum $ N _ {1} $ | ||
| + | in (9) has the bound $ \ll d ^ {a ( 1 - \sigma ) } $, | ||
| + | where $ a $ | ||
| + | is a constant; from this he deduced the existence of a constant $ c $ | ||
| + | such that any arithmetic progression $ dn + l $, | ||
| + | $ 1 \leq l \leq d $, | ||
| + | $ ( l, d) = 1 $, | ||
| + | contains a prime number less than $ d ^ {c} $. | ||
| + | The latest estimate of Linnik's constant is $ c = 17 $; | ||
| + | but if the density hypothesis is correct, i.e. if $ N _ {1} \ll ( dT) ^ {2 ( 1 - \sigma + \epsilon ) } $, | ||
| + | then $ c = 2 + \epsilon $. | ||
| − | + | In 1965, A.I. Vinogradov and Bombieri independently obtained strong estimates for $ N _ {2} $ | |
| + | in (9). A more complete method of estimating these sums was found by H. Montgomery (1969). One of the results on estimating $ N _ {2} $ | ||
| + | is the following result on the average distribution of prime numbers in arithmetic progressions: | ||
| − | + | $$ | |
| + | \sum _ {d \leq \sqrt x \mathop{\rm log} ^ {-} B x } | ||
| + | \max _ {y \leq x } \ | ||
| + | \max _ {( l, d) = 1 } \ | ||
| + | \left | | ||
| + | \psi ( y; d, l) - | ||
| + | { | ||
| + | \frac{y}{\phi ( d) } | ||
| + | } \ | ||
| + | \right | \ll \ | ||
| + | x \mathop{\rm log} ^ {-} A x, | ||
| + | $$ | ||
| − | + | $$ | |
| + | \sum _ {d \leq \sqrt x \mathop{\rm log} ^ {-} B x } \max _ {y | ||
| + | \leq x } \max _ {( l, d) = 1 } \left | \pi ( y; | ||
| + | d, l) - | ||
| + | \frac{ \mathop{\rm li} y }{\phi ( d) } | ||
| + | \right | \ll x \mathop{\rm log} ^ {-} A x, | ||
| + | $$ | ||
| − | + | for any constant $ A $ | |
| + | and $ B = A + 7/2 $. | ||
| + | These estimates cannot be substantially improved, because the extended Riemann hypothesis implies that $ B = A + 2 $. | ||
| − | + | Other problems on the distribution of prime numbers are as follows. Let $ \pi _ \nu ( x; d, l) $ | |
| + | be the number of integers of the form $ dn + l \leq x $ | ||
| + | which are products of $ \nu $ | ||
| + | prime numbers. H. Richert (1953) proved that | ||
| − | + | $$ | |
| + | \pi _ \nu ( x; d, l) = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | { | ||
| + | \frac{1}{\phi ( d) } | ||
| + | } \sum _ {m = 0 } ^ { {r } ( x) } \sum _ | ||
| + | {h = 0 } ^ { \nu - 1 } A _ \nu ( h, m, d) \int\limits _ { 2 } ^ { x } | ||
| − | + | \frac{ \mathop{\rm log} ^ {h} \mathop{\rm log} u }{ \mathop{\rm log} ^ {m + 1 } u } | |
| + | du + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | O ( x \mathop{\rm exp} (- r ( x))) + O \left ( x ^ {1 - | ||
| + | 1/bd ^ \epsilon } | ||
| + | \frac{ \mathop{\rm log} ^ {\nu - 1 } d \mathop{\rm log} ^ | ||
| + | {\nu - 1 } \mathop{\rm log} x }{\phi ( d) \mathop{\rm log} x } | ||
| + | \right ) , | ||
| + | $$ | ||
| − | where | + | where $ r ( x) = c \sqrt { \mathop{\rm log} x } $, |
| + | $ c \geq 20 $, | ||
| + | $ b = b ( \epsilon ) $, | ||
| + | $ \epsilon > 0 $, | ||
| + | and the $ A ( h, m, d) $ | ||
| + | are determined by series depending on $ h $, | ||
| + | $ m $, | ||
| + | $ d $, | ||
| + | and $ \nu $. | ||
| − | Much studied is the function | + | E. Landau (1903–1918) carried over certain results on the distribution of prime numbers to algebraic number fields. Let $ K $ |
| + | be an algebraic number field of degree $ n $ | ||
| + | and let $ \pi ( x; K) $ | ||
| + | be the number of prime ideals in $ K $ | ||
| + | with norm $ \leq x $. | ||
| + | Then | ||
| + | |||
| + | $$ | ||
| + | \pi ( x; K) = \ | ||
| + | \mathop{\rm li} x + O | ||
| + | \left ( | ||
| + | x \mathop{\rm exp} | ||
| + | \left ( | ||
| + | - { | ||
| + | \frac{c}{\sqrt n } | ||
| + | } | ||
| + | \sqrt { \mathop{\rm log} x } | ||
| + | \right ) \right ) , | ||
| + | $$ | ||
| + | |||
| + | where $ c $ | ||
| + | is an absolute positive constant, and | ||
| + | |||
| + | $$ | ||
| + | \pi ( x) - \mathop{\rm li} x = \ | ||
| + | \pm \Omega | ||
| + | |||
| + | \frac{\sqrt x }{ \mathop{\rm log} x } | ||
| + | \ | ||
| + | \mathop{\rm log} \mathop{\rm log} \mathop{\rm log} x, | ||
| + | $$ | ||
| + | |||
| + | where $ \Omega $ | ||
| + | is the negation of the symbol $ o $( | ||
| + | small). | ||
| + | |||
| + | Much studied is the function $ F ( x, y) $ | ||
| + | denoting the amount of natural numbers $ \leq x $ | ||
| + | not containing prime divisors less than $ y $. | ||
| + | For $ y = x ^ {1/ \xi } $ | ||
| + | and $ \xi = \xi ( x) \rightarrow \infty $ | ||
| + | as $ x \rightarrow \infty $, | ||
| + | such numbers are called quasi-prime numbers. By applying the sieve method to these numbers there arose a fairly complete theory of their distribution, similar to that expected from the distribution of prime numbers. The distribution of numbers with small prime divisors has also been considered (see [[#References|[15]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> L. Euler, "Einleitung in die Analysis des Unendlichen" , Springer (1983) (Translated from Latin)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.L. Chebyshev, "Oeuvres de P.L. Tchebycheff" , '''1–2''' , Chelsea (1961) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B. Riemann, "Werke" , Teubner (1892)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.E. Ingham, "The distribution of prime numbers" , Cambridge Univ. Press (1932)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A.I. Vinogradov, "Selected works" , Springer (1985) (Translated from Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> I.M. Vinogradov, "A new estimate of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033530/d033530362.png" />" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''22''' : 2 (1958) pp. 161–164 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> K. Prachar, "Primzahlverteilung" , Springer (1957)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> A.A. Karatsuba, "Fundamentals of analytic number theory" , Moscow (1975) (In Russian)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , ''Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen'' , '''1''' : 2 (1959) (Heft 13, Teil 1)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> N.G. Chudakov, "Introductions to the theory of Dirichlet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033530/d033530363.png" />-functions" , Moscow-Leningrad (1947) (In Russian)</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> A.F. Lavrik, "On the distribution of primes based on I.M. Vinogradov's method of trigonometric sums" ''Trudy Mat. Inst. Steklov.'' , '''64''' (1961) pp. 90–125 (In Russian)</TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> H. Davenport, "Multiplicative number theory" , Springer (1980)</TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974)</TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> A. Selberg, "An elementary proof of the prime-number theorem" ''Ann. of Math.'' , '''50''' (1949) pp. 305–313</TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> P. Erdös, "On a new method in elementary number theory which leads to an elementary proof of the prime number theorem" ''Proc. Nat. Acad. Sci. USA'' , '''35''' (1949) pp. 374–384</TD></TR><TR><TD valign="top">[18]</TD> <TD valign="top"> A.F. Lavrik, "Survey address" , ''Internat. Conf. on Number Theory'' , Moscow (1981) (In Russian)</TD></TR><TR><TD valign="top">[19]</TD> <TD valign="top"> H.G. Diamond, J. Steinig, "An elementary proof of the prime number theorem with a remainder term" ''Indag. Math.'' , '''11''' (1970) pp. 199–258</TD></TR><TR><TD valign="top">[20]</TD> <TD valign="top"> A.F. Lavrik, A.Sh. Sobirov, "On the remainder term in the elementary proof of the prime number theorem" ''Soviet Math. Dokl.'' , '''211''' (1973) pp. 1063–1066 ''Dokl. Akad. Nauk SSSR'' , '''211''' : 3 (1973) pp. 534–536</TD></TR><TR><TD valign="top">[21]</TD> <TD valign="top"> B. Rosser, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033530/d033530364.png" />-th prime is greater than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033530/d033530365.png" />" ''Proc. London Math. Soc. (2)'' , '''45''' (1939) pp. 21–44</TD></TR><TR><TD valign="top">[22]</TD> <TD valign="top"> Yu.V. Linnik, "The large sieve" ''Dokl. Akad. Nauk SSSR'' , '''30''' : 4 (1941) pp. 292–294 (In Russian)</TD></TR><TR><TD valign="top">[23]</TD> <TD valign="top"> Yu.V. Linnik, "On the least prime in an arithmetic progression I. The basic theorem" ''Mat. Sb.'' , '''15''' (1944) pp. 139–178 (In Russian)</TD></TR><TR><TD valign="top">[24]</TD> <TD valign="top"> A.F. Lavrik, "A survey of Linnik's large sieve and the density theory of zeros of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033530/d033530366.png" />-functions" ''Russian Math. Surveys'' , '''15''' : 2 (1980) pp. 63–76 ''Uspekhi Mat. Nauk'' , '''35''' : 2 (1980) pp. 55–65</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L. Euler, "Einleitung in die Analysis des Unendlichen" , Springer (1983) (Translated from Latin)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.L. Chebyshev, "Oeuvres de P.L. Tchebycheff" , '''1–2''' , Chelsea (1961) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B. Riemann, "Werke" , Teubner (1892)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.E. Ingham, "The distribution of prime numbers" , Cambridge Univ. Press (1932)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A.I. Vinogradov, "Selected works" , Springer (1985) (Translated from Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> I.M. Vinogradov, "A new estimate of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033530/d033530362.png" />" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''22''' : 2 (1958) pp. 161–164 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> K. Prachar, "Primzahlverteilung" , Springer (1957)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> A.A. Karatsuba, "Fundamentals of analytic number theory" , Moscow (1975) (In Russian)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , ''Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen'' , '''1''' : 2 (1959) (Heft 13, Teil 1)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> N.G. Chudakov, "Introductions to the theory of Dirichlet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033530/d033530363.png" />-functions" , Moscow-Leningrad (1947) (In Russian)</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> A.F. Lavrik, "On the distribution of primes based on I.M. Vinogradov's method of trigonometric sums" ''Trudy Mat. Inst. Steklov.'' , '''64''' (1961) pp. 90–125 (In Russian)</TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> H. Davenport, "Multiplicative number theory" , Springer (1980)</TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974)</TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> A. Selberg, "An elementary proof of the prime-number theorem" ''Ann. of Math.'' , '''50''' (1949) pp. 305–313</TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> P. Erdös, "On a new method in elementary number theory which leads to an elementary proof of the prime number theorem" ''Proc. Nat. Acad. Sci. USA'' , '''35''' (1949) pp. 374–384</TD></TR><TR><TD valign="top">[18]</TD> <TD valign="top"> A.F. Lavrik, "Survey address" , ''Internat. Conf. on Number Theory'' , Moscow (1981) (In Russian)</TD></TR><TR><TD valign="top">[19]</TD> <TD valign="top"> H.G. Diamond, J. Steinig, "An elementary proof of the prime number theorem with a remainder term" ''Indag. Math.'' , '''11''' (1970) pp. 199–258</TD></TR><TR><TD valign="top">[20]</TD> <TD valign="top"> A.F. Lavrik, A.Sh. Sobirov, "On the remainder term in the elementary proof of the prime number theorem" ''Soviet Math. Dokl.'' , '''211''' (1973) pp. 1063–1066 ''Dokl. Akad. Nauk SSSR'' , '''211''' : 3 (1973) pp. 534–536</TD></TR><TR><TD valign="top">[21]</TD> <TD valign="top"> B. Rosser, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033530/d033530364.png" />-th prime is greater than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033530/d033530365.png" />" ''Proc. London Math. Soc. (2)'' , '''45''' (1939) pp. 21–44</TD></TR><TR><TD valign="top">[22]</TD> <TD valign="top"> Yu.V. Linnik, "The large sieve" ''Dokl. Akad. Nauk SSSR'' , '''30''' : 4 (1941) pp. 292–294 (In Russian)</TD></TR><TR><TD valign="top">[23]</TD> <TD valign="top"> Yu.V. Linnik, "On the least prime in an arithmetic progression I. The basic theorem" ''Mat. Sb.'' , '''15''' (1944) pp. 139–178 (In Russian)</TD></TR><TR><TD valign="top">[24]</TD> <TD valign="top"> A.F. Lavrik, "A survey of Linnik's large sieve and the density theory of zeros of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033530/d033530366.png" />-functions" ''Russian Math. Surveys'' , '''15''' : 2 (1980) pp. 63–76 ''Uspekhi Mat. Nauk'' , '''35''' : 2 (1980) pp. 55–65</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | In formula (7) above, | + | In formula (7) above, $ \Lambda ( n) $ |
| + | is the (von) [[Mangoldt function|Mangoldt function]], which has the value $ \mathop{\rm log} p $ | ||
| + | if $ n $ | ||
| + | is a prime power $ p ^ {m} $ | ||
| + | and is zero otherwise. | ||
Concerning estimates of trigonometric sums see also [[Trigonometric sums, method of|Trigonometric sums, method of]]. | Concerning estimates of trigonometric sums see also [[Trigonometric sums, method of|Trigonometric sums, method of]]. | ||
| − | Some more facts. Although numerical tables do not suggest it, the function | + | Some more facts. Although numerical tables do not suggest it, the function $ \pi ( x) - \mathop{\rm li} ( x) $ |
| + | changes sign infinitely often. This was shown by Littlewood. By the work of H. Iwaniec, J. Pintz and C.J. Mozzochi it is now (1986) known that $ d _ {n} \ll p _ {n} ^ \theta $ | ||
| + | with $ \theta = 11/12 - 1/384 $. | ||
| + | The largest known prime twin is $ 1639494 ( 2 ^ {4423} - 1) \pm 1 $( | ||
| + | W. Keller, 1983). | ||
Many interesting facts, both computationally and theoretically, on the distribution of primes can be found in [[#References|[a5]]], which is written in an elementary style. For elementary methods one can also consult [[#References|[a1]]]. In [[#References|[a4]]] one finds a simple proof of the prime number theorem. | Many interesting facts, both computationally and theoretically, on the distribution of primes can be found in [[#References|[a5]]], which is written in an elementary style. For elementary methods one can also consult [[#References|[a1]]]. In [[#References|[a4]]] one finds a simple proof of the prime number theorem. | ||
| − | The fact that there are infinitely many primes (i.e. | + | The fact that there are infinitely many primes (i.e. $ \pi ( x) \rightarrow \infty $ |
| + | as $ x \rightarrow \infty $) | ||
| + | is also known as the [[Euclidean prime number theorem|Euclidean prime number theorem]]. The prime number theorem states that $ \pi ( x) $ | ||
| + | is asymptotically equal to $ x ( \mathop{\rm log} x) ^ {-} 1 $( | ||
| + | cf. also [[De la Vallée-Poussin theorem|de la Vallée-Poussin theorem]]). The Dirichlet prime number theorem states that there are infinitely many primes in every arithmetic progression (i.e. $ \pi ( x; d, l) \rightarrow \infty $ | ||
| + | as $ x \rightarrow \infty $). | ||
For the result of Bombieri–Vinogradov see also (the references to) [[Density hypothesis|Density hypothesis]]. | For the result of Bombieri–Vinogradov see also (the references to) [[Density hypothesis|Density hypothesis]]. | ||
Revision as of 19:36, 5 June 2020
2020 Mathematics Subject Classification: Primary: 11N05 [MSN][ZBL]
A branch of number theory studying distribution laws of prime numbers among natural numbers. The central problem is that of finding the best asymptotic, as $ x \rightarrow \infty $, expression for the function $ \pi ( x) $, which is the number of prime numbers not exceeding $ x $, and for the function $ \pi ( x; d, l) $, which is the number of prime numbers not exceeding $ x $ in the arithmetic progression $ dn + l $, $ 1 \leq l \leq d $, $ n = 1, 2 \dots $ for values of $ d $ increasing along with $ x $.
The fundamental theorem of arithmetic: Any natural number $ n > 1 $ is either a prime number or a unique (up to permutation of factors) product
$$ n = \ p _ {1} ^ {n _ {1} } \dots p _ {k} ^ {n _ {k} } $$
(the so-called canonical representation of $ n $), where $ p _ {1} \dots p _ {k} $ are different prime numbers and $ n _ {1} \dots n _ {k} $ are natural numbers. Thus, the prime numbers form a multiplicative basis for the set of natural numbers. This, though, says nothing about the value of $ \pi ( x) $.
A method used for finding the prime numbers between 1 and $ x $ is that of the sieve of Eratosthenes, known since the 3rd century B.C. (cf. Eratosthenes, sieve of). The sieve of Eratosthenes is the simplest procedure for obtaining the sequence of prime numbers. But the analytic formula of the sieve,
$$ \pi ( x) - \pi ( \sqrt x ) + 1 = \ \sum _ { d } (- 1) ^ {\nu ( d) } \left [ { \frac{x}{d} } \right ] , $$
where $ d $ takes the values of the divisors of the product of all prime numbers $ \leq \sqrt x $; $ \nu ( d) $ is the number of prime divisors of $ d $ and $ [ u] $ is the integer part of $ u $, is not very well suited for studying $ \pi ( x) $ as $ x \rightarrow \infty $.
The examination of the sequence of prime numbers between 1 and $ x $:
$$ \tag{1 } 2, 3, 5, 7, 11, 13 \dots p, $$
shows that they get ever sparser on the average as $ x $ increases. There are arbitrarily long segments of the natural series containing no prime number. For instance, the $ n - 1 $ numbers of the form $ n! + 2 \dots n! + n $ are all composite for any $ n \geq 2 $. At the same time, prime numbers that differ by 2, like 8004119 and 8004121, are encountered in (1) (twins). The behaviour of $ \pi ( x) $ as $ x \rightarrow \infty $ is one of the most difficult and inspiring problems of number theory.
The first result about $ \pi ( x) $ is Euclid's theorem: $ \pi ( x) \rightarrow \infty $ as $ x \rightarrow \infty $. L. Euler (1737, 1749, see [1]) introduced the function
$$ \tag{2 } \zeta ( s) = \ \sum _ {n = 1 } ^ \infty n ^ {-} s $$
and showed that
$$ \tag{3 } \zeta ( s) = \ \prod _ { p } \left ( 1 - { \frac{1}{p ^ {s} } } \right ) ^ {-} 1 $$
for $ s > 1 $. Here the series extends over all natural numbers, and the product over all prime numbers. The identity (3) and its generalizations play a fundamental role in the theory of the distribution of prime numbers. Based on the identity, Euler proved that the series $ \sum 1/p $ and the product $ \prod ( 1 - 1/p) ^ {-} 1 $ diverge over the sequence of prime numbers. This is another proof that the set of prime numbers is infinite. Moreover, Euler proved that
$$ \pi ( x) > \mathop{\rm log} { \frac{x}{e} } , $$
which shows that there are "many" prime numbers, although almost-all natural numbers are composite in the sense that
$$ { \frac{\pi ( x) }{x} } \rightarrow 0 \ \ \textrm{ as } x \rightarrow \infty . $$
A significant success was subsequently obtained by P.L. Chebyshev (1851–1852, see [2]). He proved that
1) for any $ m, M > 0 $ there are sequences $ x, y \rightarrow \infty $ such that
$$ \pi ( x) - \mathop{\rm li} x < \ Mx \mathop{\rm log} ^ {-} m x, $$
$$ \pi ( y) - \mathop{\rm li} y > - My \mathop{\rm log} ^ {-} m y; $$
2) if the quotient $ ( \pi ( x) \mathop{\rm log} x)/x $ converges as $ x \rightarrow \infty $, then the limit is equal to 1.
This solved for the first time the question of the existence of a simple function
$$ \mathop{\rm li} x \equiv \ \int\limits _ { 2 } ^ { x } \frac{du }{ \mathop{\rm log} u } = \ { \frac{x}{ \mathop{\rm log} x } } + \dots + \frac{( r - 1)! x }{ \mathop{\rm log} ^ {r} x } + O \left ( { \frac{x}{ \mathop{\rm log} ^ {r + 1 } x } } \right ) , $$
which approximates $ \pi ( x) $ optimally.
Then Chebyshev established the true order of growth of $ \pi ( x) $, that is, the existence of constants $ a > 0 $ and $ A > 0 $ such that
$$ \tag{4 } a { \frac{x}{ \mathop{\rm log} x } } < \ \pi ( x) < \ A { \frac{x}{ \mathop{\rm log} x } } ; $$
notably, $ a = 0.92 \dots $, $ A = 1.05 \dots $ for $ x \geq x _ {0} $. He also proved that for any $ n \geq 2 $ the interval $ ( n, 2n) $ contains at least one prime number (Bertrand's postulate). The proof of (4) is based on Chebyshev's identity
$$ \tag{5 } F ( x) \equiv \ \mathop{\rm log} [ x]! = \ \sum _ {n \leq x } \psi \left ( { \frac{x}{n} } \right ) , $$
where the function $ \psi $, introduced by Chebyshev, is defined by the sum
$$ \psi ( x) = \ \sum _ {p ^ {m} \leq x } \mathop{\rm log} p = \ \sum _ {n < x } \Delta ( n), $$
taken over all powers $ p ^ {m} $, $ m \in \mathbf N $, of prime numbers $ p $. Namely, if $ x \geq 30 $, the following combination of $ \mathop{\rm log} [ u]! $:
$$ F ^ { * } ( x) = \ F ( x) + F \left ( { \frac{x}{30} } \right ) - F \left ( { \frac{x}{2} } \right ) - F \left ( { \frac{x}{3} } \right ) - F \left ( { \frac{x}{6} } \right ) , $$
owing to (5), gives the identity
$$ F ^ { * } ( x) = \ \psi ( x) - \psi \left ( { \frac{x}{6} } \right ) + \psi \left ( { \frac{x}{7} } \right ) - \psi \left ( { \frac{x}{10} } \right ) + \dots , $$
which implies
$$ \psi ( x) - \psi \left ( { \frac{x}{6} } \right ) < \ F ^ {*} ( x) < \ \psi ( x). $$
By virtue of Stirling's asymptotic formula for $ n! $ this implies an analogue of (4) for $ \psi ( x) $ from which (4) is obtained by partial summation. Chebyshev's function $ \psi ( x) $ proved to be more convenient for studying the distribution of prime numbers than $ \pi ( x) $, since the best approximation for it is the very argument $ x $. Therefore $ \psi ( x) $ is usually considered first and then the corresponding result for $ \pi ( x) $ is obtained by partial summation.
Riemann's principle.
In 1859–1860 B. Riemann [3] considered the function $ \zeta ( s) $, introduced by Euler for $ s > 1 $, as a function of a complex variable $ s = \sigma + it $, where $ \sigma $ and $ t $ are real variables, defined by (2) for $ \sigma > 1 $( see Zeta-function) and found that this function is extremely important in the theory of the distribution of prime numbers. In particular, he found an expression for the difference $ \pi ( x) - \mathop{\rm li} x $ in terms of $ x $ and those zeros of $ \zeta ( s) $ which belong to the strip $ 0 \leq \sigma \leq 1 $; they are called the non-trivial zeros of $ \zeta ( s) $.
Instead of Riemann's formula, its simpler finite analogue for $ \psi ( x) $, proved (along with Riemann's formula) by H. (von) Mangoldt in 1895, is often used. Namely, for $ x > 1 $:
$$ \tag{6 } \psi ( x) = x - \sum _ {| \gamma | \leq T } { \frac{x ^ \rho } \rho } + O \left ( { \frac{x}{T} } \ \mathop{\rm log} ^ {2} xT + \mathop{\rm log} 2x \right ) , $$
where $ \rho = \rho + i \gamma $ runs through the non-trivial zeros of $ \zeta ( s) $ and $ T \geq 2 $ is arbitrary.
Since
$$ \sum _ {| \gamma | \leq T } { \frac{1} \gamma } \ll \ \mathop{\rm log} ^ {2} T, $$
(6) shows that the difference $ \psi ( x) - x $ is primarily defined by $ \beta $( the real part of the right-most zeros $ \rho $). In particular, the following asymptotic expressions are valid for $ \psi ( x) $ and $ \pi ( x) $:
$$ \psi ( x) = \ x + O ( x ^ \theta \ \mathop{\rm log} ^ {2} x), $$
$$ \pi ( x) = \mathop{\rm li} x + O ( x ^ \theta \mathop{\rm log} x), $$
provided that $ \zeta ( x) \neq 0 $ to the right of a vertical $ \sigma = \theta $, $ 1/2 \leq \theta < 1 $. Conversely, it follows from these relations that $ \zeta ( s) \neq 0 $ if $ \sigma \geq \theta $. If the Riemann hypothesis holds, that is, if all non-trivial zeros of $ \zeta ( s) $ lie on the line $ \sigma = 1/2 $, then the asymptotic distribution law for prime numbers must have the form
$$ \psi ( x) = \ x + O ( \sqrt x \ \mathop{\rm log} ^ {2} x), $$
$$ \pi ( x) = \mathop{\rm li} x + O ( \sqrt x \mathop{\rm log} x), $$
and these relations cannot be substantially strengthened. The latter means that there are sequences $ x, y \rightarrow \infty $ such that
$$ \pi ( x) - \mathop{\rm li} x < \ - \sqrt x \frac{ \mathop{\rm log} \mathop{\rm log} \mathop{\rm log} x }{ \mathop{\rm log} \mathop{\rm log} x } , $$
$$ \pi ( y) - \mathop{\rm li} y > + y \frac{ \mathop{\rm log} \mathop{\rm log} \mathop{\rm log} y }{ \mathop{\rm log} \mathop{\rm log} y } . $$
Thus, by Riemann's principle, the problem about the asymptotic expressions for $ \psi ( x) $ and $ \pi ( x) $ reduces to that about bounds for the real part of the non-trivial zeros of $ \zeta ( x) $. Till now (1983), however, no constant $ \theta $, $ 1/2 \leq \theta < 1 $, has been found with the condition $ \beta < \theta $. The desired bound for $ \beta $ turns out to be connected with the imaginary part $ \gamma $ of zeros $ \rho $ in such a way that the line $ \sigma = 1 $ is its asymptote.
The methods of Hadamard and de la Vallée-Poussin.
In its simplest form
$$ \lim\limits _ {x \rightarrow \infty } \ { \frac{\pi ( x) \mathop{\rm log} x }{x} } = \ \lim\limits _ {x \rightarrow \infty } \ { \frac{\psi ( x) }{x} } = 1 $$
the asymptotic distribution law for prime numbers was independently obtained in 1896 by J. Hadamard and Ch.J. de la Vallée-Poussin, who proved that $ \zeta ( 1 + it) \neq 0 $, that is, there is no zero of $ \zeta ( s) $ on the line $ \sigma = 1 $. In 1899 de la Vallée-Poussin showed that $ \zeta ( \sigma + it) \neq 0 $ in the domain $ \sigma \geq 1 - c/ \mathop{\rm log} ( | t | + 2) $. It was thereby proved that
$$ \psi ( x) = x + O ( x \mathop{\rm exp} (- a \sqrt { \mathop{\rm log} x } )), $$
$$ \pi ( x) = \mathop{\rm li} x + O ( x \mathop{\rm exp} (- b \sqrt { \mathop{\rm log} x } )) , $$
where $ a, b > 0 $ are constants.
Further extensions of the region containing no zeros of $ \zeta ( s) $ were also obtained (see [4]–[12]).
The method of Weyl–Littlewood.
There is a certain connection between the growth of the modulus of $ \zeta ( s) $ and its zeros near the line $ \sigma = 1 $. In particular, if $ | \zeta ( s) | \ll \mathop{\rm exp} \phi ( t) $ for $ 1 - \theta ( t) \leq \sigma \leq 2 $, where $ \phi ( t) $ and $ 1/ \theta ( t) $ are positive non-decreasing functions of $ t \geq 0 $ such that $ \theta ( t) \leq 1 $, $ \phi ( t) \rightarrow \infty $ as $ t \rightarrow \infty $ and $ \phi ( t)/ \theta ( t) \ll \mathop{\rm exp} \phi ( t) $, then there is a constant $ A $ such that $ \zeta ( s) \neq 0 $ in the region
$$ \sigma \geq 1 - \frac{A \theta ( 2t + 1) }{\phi ( 2t + 1) } . $$
The estimate for $ \zeta ( s) $ is here obtained with the help of the partial sums of the series (2). This reduces the problem to the estimation of trigonometric sums of the form
$$ \sum _ {v < n \leq u } \mathop{\rm exp} ( it \mathop{\rm log} n). $$
By estimating such sums by the Weyl method, J.E. Littlewood showed in 1921 that $ | \zeta ( s) | \ll \mathop{\rm log} ^ {5} t $ if $ t > A $ and $ \sigma \geq 1 - \mathop{\rm log} ^ {2} \mathop{\rm log} t/ \mathop{\rm log} t $, so that $ \zeta ( s) \neq 0 $ in the region
$$ \sigma \geq 1 - \frac{A \mathop{\rm log} \mathop{\rm log} t }{ \mathop{\rm log} t } . $$
It follows that
$$ \pi ( x) = \ \mathop{\rm li} x + O ( x \mathop{\rm exp} (- a \sqrt { \mathop{\rm log} x \mathop{\rm log} \mathop{\rm log} x } )). $$
The method of Vinogradov.
A further advance in the estimation of $ \pi ( x) $ and $ \psi ( x) $ is connected with development by I.M. Vinogradov of a new and substantially more powerful method for the estimation of trigonometric sums (see Vinogradov method). Using this method, he showed in 1938 that $ \zeta ( s) \neq 0 $ if
$$ \sigma \geq 1 - { \frac{c}{ \mathop{\rm log} ^ {3/4} ( | t | + 2) \ \mathop{\rm log} ^ {3/4} \mathop{\rm log} ( | t | + 2) } } , $$
and consequently that
$$ \pi ( x) = \ \mathop{\rm li} x + O ( x \mathop{\rm exp} (- a \ \mathop{\rm log} ^ {4/7} x \ \mathop{\rm log} ^ {-} 3/7 \ \mathop{\rm log} x)). $$
In 1958 Vinogradov and others (see [6]–[11]) showed that $ \zeta ( s) \neq 0 $ if
$$ \sigma \geq 1 - { \frac{c}{ \mathop{\rm log} ^ {2/3} ( | t | + 2) \ \mathop{\rm log} ^ {1/3} \mathop{\rm log} ( | t | + 2) } } . $$
So far (1983) this is the best result concerning bounds on the non-trivial zeros of $ \zeta ( s) $, to which the following best result on the distribution of prime numbers corresponds:
$$ \pi ( x) = \ \mathop{\rm li} x + O ( x \mathop{\rm exp} (- a \mathop{\rm log} ^ {3/5} \ x \mathop{\rm log} ^ {-} 1/5 \ \mathop{\rm log} x)), $$
$$ \psi ( x) = x + O ( x \mathop{\rm exp} (- b \mathop{\rm log} ^ {3/5} x \mathop{\rm log} ^ {-} 1/5 \mathop{\rm log} x)). $$
The asymptotics for the $ n $- th prime number, $ p _ {n} \sim n \mathop{\rm log} n $, follow from the asymptotics of $ \pi ( x) $. It was also shown (see [21]) that $ p _ {n} > n \mathop{\rm log} n $ for all $ n \geq 1 $ and that for $ 17 \leq x \leq e ^ {100} $, $ x \geq e ^ {200} $,
$$ { \frac{x}{ \mathop{\rm log} x } } < \ \pi ( x) < \ { \frac{x}{ \mathop{\rm log} x - 2 } } ; $$
and for $ x \geq 55 $,
$$ { \frac{x}{ \mathop{\rm log} x + 2 } } < \ \pi ( x) < \ { \frac{x}{ \mathop{\rm log} x - 4 } } . $$
Elementary methods.
This is the name for methods for studying the asymptotic distribution of prime numbers that are not based on Riemann's principle (zeros of the zeta-function) and, in general, on any principles from the theory of functions of a complex variable whatsoever. Such a method was first discovered by A. Selberg [16] and P. Erdös [17]. It is based on the elementary formula of Selberg
$$ \tag{7 } \psi ( x) \mathop{\rm log} x + \sum _ {n \leq x } \psi \left ( { \frac{x}{n} } \right ) \Lambda ( n) = \ 2x \mathop{\rm log} x + O ( x). $$
A further problem consists in obtaining asymptotics for $ \psi ( x) $ from the averaged asymptotics for $ \psi ( u) $ given by (7). It may be done in different ways but all of them employ the fact that $ \psi ( x) $ slowly oscillates. In 1962 E. Bombieri and E. Wirsing proved that
$$ \psi ( x) = \ x + O ( x \mathop{\rm log} ^ {-} A x) $$
for any fixed $ A > 0 $. In 1970, H.G. Diamond and J. Steinig [19] substantially perfected the principles and techniques of estimation by means of an elementary method. They proved that for $ x \geq \mathop{\rm exp} \mathop{\rm exp} 100 $,
$$ | \psi ( x) - x | < \ x \mathop{\rm exp} (- \mathop{\rm log} ^ {1/7} \ x \mathop{\rm log} ^ {-} 2 \mathop{\rm log} x). $$
Finally, in 1973 A.F. Lavrik and A.Sh. Sobirov [20] showed that an elementary method enables one to prove the following theorem: For $ x \geq \mathop{\rm exp} \mathop{\rm exp} 10 ^ {3} $,
$$ | \psi ( x) - x | < \ x \mathop{\rm exp} (- \mathop{\rm log} ^ {1/6} \ x \mathop{\rm log} ^ {-} 3 \mathop{\rm log} x). $$
This result is so far the best achievement of the elementary method as regards the distribution of prime numbers. Although it is somewhat weaker than the result obtained by the analytic method, in principle they are close.
The difference between prime numbers.
There are many questions in the distribution of prime numbers that are concerned with differences between prime numbers. Standing out among them are questions about the behaviour of the difference $ d _ {n} = p _ {n + 1 } - p _ {n} $ between adjacent prime numbers; the problem on the number of prime twins or, more generally, pairs of prime numbers that differ by $ 2k $ or, in the most general form, the problem about the number of systems $ p, p + u _ {1} \dots p + u _ {m} $ of $ m + 1 $ prime numbers within the segment $ [ 1, x] $.
Using Riemann's hypothesis it was proved that $ d _ {n} \ll \sqrt {p _ {n} } \mathop{\rm log} p _ {n} $, and heuristic considerations suggest that probably $ d _ {n} \ll \mathop{\rm log} ^ {2} p _ {n} $. By 1983, the best estimate $ d _ {n} \ll p _ {n} ^ \delta $, where $ \delta = ( 7/12) + \epsilon $, $ \epsilon > 0 $, was obtained by M.N. Huxley (1973) using the method of the large sieve. As for pairs of prime numbers whose difference is equal to 2 (twins) or to $ 2k $, $ k = 1, 2 \dots $ it is still (1983) unknown whether the number of such pairs is finite or not. Let $ \pi _ {k} ( x) $ be the number of prime numbers that do not exceed $ x $ and differ by $ 2k $. In 1919 V. Brun found a sieve method (see Brun sieve) that permitted one to obtain the expected upper bound for $ \pi _ {k} ( x) $:
$$ \pi _ {k} ( x) \ll \ { \frac{x}{ \mathop{\rm log} ^ {2} x } } \prod _ { p\mid } k \left ( 1 - { \frac{1}{p} } \right ) ^ {-} 1 . $$
In addition to that, it was shown by the circle method (see [13]) with the help of Vinogradov's estimates for trigonometric sums with prime numbers (see Vinogradov method) that for any fixed $ A > 1 $, $ M > 0 $,
$$ \sum _ {1 \leq 2h \leq x \mathop{\rm log} ^ {-} A x } \left [ \pi _ {k} ( x) - f ( x) \prod _ {\begin{array}{c} p\mid k \\ p > 2 \end{array} } \frac{p - 1 }{p - 2 } \right ] ^ {2} \ll \ x ^ {3} \mathop{\rm log} ^ {- A - M } x, $$
where
$$ f ( x) = 2 \prod _ {p > 2 } \left ( 1 - { \frac{1}{( p - 1) ^ {2} } } \right ) \int\limits _ { 2 } ^ { x } \frac{du }{ \mathop{\rm log} ^ {2} u } . $$
This implies, in particular, that for $ X = x \mathop{\rm log} ^ {-} A x $ the following asymptotic expression for $ \pi _ {k} ( x) $ holds for all $ 1 \leq k \leq X $ except for at most $ X \mathop{\rm log} ^ {-} M x $ values of $ k $ in the range $ 1 \leq k \leq X $:
$$ \pi _ {k} ( x) \sim 2 \prod _ {p > 2 } \left ( 1 - { \frac{1}{( p - 1) ^ {2} } } \right ) { \frac{x}{ \mathop{\rm log} ^ {2} x } } \prod _ {\begin{array}{c} p\mid k \\ p > 2 \end{array} } \frac{p - 1 }{p - 2 } . $$
Similar results are obtained for sets of prime numbers $ p, p + u _ {1} \dots p + u _ {m} $ for all $ m \geq 1 $.
Prime numbers in arithmetic progressions.
The first method (of Euclid) for proving the infinitude of prime numbers can also be applied to certain arithmetic progressions. But the proof by this method that every arithmetic progression $ dn + l $, where the first number $ l $ and the difference $ d $ are relatively prime, contains infinitely many prime numbers has not yet (1983) been given. The problem was solved by another method by P. Dirichlet (1837–1840), who extended an idea of Euler in showing that $ \sum 1/p ^ {s} \rightarrow \infty $ as $ s \rightarrow 1 + 0 $ for prime numbers $ p \equiv l ( \mathop{\rm mod} d) $. To do this he introduced certain arithmetical functions — characters $ \chi = \chi ( n, d) $( see Dirichlet character) and functions $ L ( s, \chi ) $( see Dirichlet $ L $- function), which, like $ \zeta ( s) $ for $ \pi ( x) $ and $ \psi ( x) $, serve as a basic means of studying $ \pi ( x; d, l) $ and its analogue
$$ \psi ( x; d, l) = \ \sum _ {\begin{array}{c} n \leq x, \\ n \equiv l ( \mathop{\rm mod} d) \end{array} } \Lambda ( n). $$
For a fixed value of $ d $, $ 1 \leq l \leq d $, $ ( l, d) = 1 $, the majority of results indicated above for $ \pi ( x) $ and $ \psi ( x) $ carry over to $ \pi ( x; d, l) $ and $ \psi ( x; d, l) $. However, of special interest here are the results for values of $ d $ that increase with $ x $, as these are important in additive number theory and elsewhere. In this case, other significant difficulties arise, connected mostly with estimating $ d $, the largest real zero of $ L ( s, \chi ) $ modulo $ d $. It can be proved using the Page theorem that for $ 1 \leq d \leq ( \mathop{\rm log} x) ^ {2 - \epsilon } $, $ 0 < \epsilon < 1/2 $,
$$ \psi ( x; d, l) = \ { \frac{x}{\phi ( d) } } + O ( x \mathop{\rm exp} (- a \ \mathop{\rm log} ^ {\epsilon /3 } x)), $$
and as a result of C.L. Siegel's bound (1935), for any fixed $ A > 1 $, for $ 1 \leq d \leq \mathop{\rm log} ^ {A} x $,
$$ \psi ( x; d, l) = \ { \frac{x}{\phi ( d) } } + O ( x \mathop{\rm exp} (- c _ {1} \sqrt { \mathop{\rm log} x } )), $$
where $ \phi ( d) $ is the Euler $ \phi $- function, $ a $ is a positive constant and $ c _ {1} = c _ {1} ( A) $ is an ineffective constant $ > 0 $, that is, $ c _ {1} $ cannot be computed for given $ A $.
If the extended Riemann hypothesis (cf. Riemann hypotheses) is true, then for $ d \leq x $,
$$ \psi ( x; d, l) = \ { \frac{x}{\phi ( d) } } + O ( \sqrt x \mathop{\rm log} ^ {2} x). $$
Thus, up till 1983 it has been proved that the prime numbers are uniformly distributed over all $ \phi ( d) $ progressions $ 1 \leq l \leq d $, $ ( l, d) = 1 $, of difference $ d $ only for $ d \leq \mathop{\rm log} ^ {A} x $. As far as segments of progressions $ dn + l \leq x $ are concerned, for example with $ d = x ^ \epsilon $ for any $ \epsilon > 0 $, it does not even follow from the above that such a progression contains at least one prime number.
The sieve method of Brun, like the modification suggested by Selberg in 1947, shows that for all $ 1 \leq d < x $, $ 1 \leq l \leq d $, $ ( l, d) = 1 $, there is an upper bound
$$ \pi ( x; d, l) \ll \ \frac{Cx }{\phi ( d) \mathop{\rm log} { \frac{x}{d} } } , $$
with absolute constant $ C $, but no lower bounds for $ \pi ( x; d, l) $ are obtainable by these methods.
By the Riemann principle for a zero $ \rho = \beta + i \gamma $ of $ L ( s, \chi ) $ lying in the strip $ 0 \leq \sigma \leq 1 $, $ \psi ( x; d, l) $ has the form
$$ \tag{8 } \psi ( x; d, l) = \ \frac{\psi ( x) }{\phi ( d) } + $$
$$ - { \frac{1}{\phi ( d) } } \left ( \sum _ \chi {} \prime \overline \chi \; ( l) \sum _ {| \gamma | \leq T } { \frac{x ^ \rho } \rho } + { \frac{\overline \chi \; ( l) x ^ \alpha } \alpha } \right ) + R, $$
where the prime on the $ \sum $ indicates summation over complex $ \chi $ $ \mathop{\rm mod} d $, $ \alpha $ is the real zero of $ L ( s, \chi ) $ if it exists and is greater than $ 1 - C _ {0} / \mathop{\rm log} d $, and
$$ R \ll xT ^ {-} 1 \ \mathop{\rm log} ^ {2} dx + x ^ {1/4} \mathop{\rm log} x, $$
for any $ T \geq 2 $.
From (8) one sees that if one disregards the term corresponding to $ \alpha $, the remainder term is determined by the double sum and depends also on the real part of $ \rho $ and on all the $ L ( x, \chi ) $ with $ \chi $ $ \mathop{\rm mod} d $ having a zero $ \rho $ with $ \mathop{\rm Re} \rho = \beta $. If, for $ 0.5 \leq \sigma \leq 1 $, $ N ( \sigma , T, \chi ) $ denotes the number of zeros of $ L ( s, \chi ) $ in the rectangle $ \sigma \leq \mathop{\rm Re} s \leq 1 $, $ | t | \leq T $, then the problem of estimating the remainder term for $ \psi ( x; d, l) $ and its mean value is reduced to the problem of estimating the density of the distribution of the zeros of $ L $- functions:
$$ \tag{9 } \left . \begin{array}{c} N _ {1} \equiv \ \sum _ {\chi \mathop{\rm mod} d } {} \prime N ( \sigma , T, \chi ), \\ N _ {2} \equiv \ \sum _ {d \leq D } \ \sum _ {\chi \mathop{\rm mod} d } {} \prime N ( \sigma , T, \chi ). \\ \end{array} \right \} $$
Thus, the reduction of various estimates for prime numbers is concerned not so much with the lack of zeros of $ L ( s, \chi ) $ in the critical strip, but with their comparatively rare distribution there.
The realization of this idea has been one of the central directions of research on the distribution of prime numbers over the last forty years. A start was made by Yu.V. Linnik with his discovery in 1941 of the method of the large sieve (see [22], and also [14], [24]). Especially important are the theorems on the least prime number in an arithmetic progression, the behaviour of $ \pi ( x; d, l) $ and $ \psi ( x; d, l) $ on the average for $ d \leq D $, and on the double averaging of these functions over $ 1 \leq l \leq d $, $ ( l, d) = 1 $, and over $ d \leq D $.
Namely, in 1944 Linnik [23] showed that as $ d \rightarrow \infty $ the sum $ N _ {1} $ in (9) has the bound $ \ll d ^ {a ( 1 - \sigma ) } $, where $ a $ is a constant; from this he deduced the existence of a constant $ c $ such that any arithmetic progression $ dn + l $, $ 1 \leq l \leq d $, $ ( l, d) = 1 $, contains a prime number less than $ d ^ {c} $. The latest estimate of Linnik's constant is $ c = 17 $; but if the density hypothesis is correct, i.e. if $ N _ {1} \ll ( dT) ^ {2 ( 1 - \sigma + \epsilon ) } $, then $ c = 2 + \epsilon $.
In 1965, A.I. Vinogradov and Bombieri independently obtained strong estimates for $ N _ {2} $ in (9). A more complete method of estimating these sums was found by H. Montgomery (1969). One of the results on estimating $ N _ {2} $ is the following result on the average distribution of prime numbers in arithmetic progressions:
$$ \sum _ {d \leq \sqrt x \mathop{\rm log} ^ {-} B x } \max _ {y \leq x } \ \max _ {( l, d) = 1 } \ \left | \psi ( y; d, l) - { \frac{y}{\phi ( d) } } \ \right | \ll \ x \mathop{\rm log} ^ {-} A x, $$
$$ \sum _ {d \leq \sqrt x \mathop{\rm log} ^ {-} B x } \max _ {y \leq x } \max _ {( l, d) = 1 } \left | \pi ( y; d, l) - \frac{ \mathop{\rm li} y }{\phi ( d) } \right | \ll x \mathop{\rm log} ^ {-} A x, $$
for any constant $ A $ and $ B = A + 7/2 $. These estimates cannot be substantially improved, because the extended Riemann hypothesis implies that $ B = A + 2 $.
Other problems on the distribution of prime numbers are as follows. Let $ \pi _ \nu ( x; d, l) $ be the number of integers of the form $ dn + l \leq x $ which are products of $ \nu $ prime numbers. H. Richert (1953) proved that
$$ \pi _ \nu ( x; d, l) = $$
$$ = \ { \frac{1}{\phi ( d) } } \sum _ {m = 0 } ^ { {r } ( x) } \sum _ {h = 0 } ^ { \nu - 1 } A _ \nu ( h, m, d) \int\limits _ { 2 } ^ { x } \frac{ \mathop{\rm log} ^ {h} \mathop{\rm log} u }{ \mathop{\rm log} ^ {m + 1 } u } du + $$
$$ + O ( x \mathop{\rm exp} (- r ( x))) + O \left ( x ^ {1 - 1/bd ^ \epsilon } \frac{ \mathop{\rm log} ^ {\nu - 1 } d \mathop{\rm log} ^ {\nu - 1 } \mathop{\rm log} x }{\phi ( d) \mathop{\rm log} x } \right ) , $$
where $ r ( x) = c \sqrt { \mathop{\rm log} x } $, $ c \geq 20 $, $ b = b ( \epsilon ) $, $ \epsilon > 0 $, and the $ A ( h, m, d) $ are determined by series depending on $ h $, $ m $, $ d $, and $ \nu $.
E. Landau (1903–1918) carried over certain results on the distribution of prime numbers to algebraic number fields. Let $ K $ be an algebraic number field of degree $ n $ and let $ \pi ( x; K) $ be the number of prime ideals in $ K $ with norm $ \leq x $. Then
$$ \pi ( x; K) = \ \mathop{\rm li} x + O \left ( x \mathop{\rm exp} \left ( - { \frac{c}{\sqrt n } } \sqrt { \mathop{\rm log} x } \right ) \right ) , $$
where $ c $ is an absolute positive constant, and
$$ \pi ( x) - \mathop{\rm li} x = \ \pm \Omega \frac{\sqrt x }{ \mathop{\rm log} x } \ \mathop{\rm log} \mathop{\rm log} \mathop{\rm log} x, $$
where $ \Omega $ is the negation of the symbol $ o $( small).
Much studied is the function $ F ( x, y) $ denoting the amount of natural numbers $ \leq x $ not containing prime divisors less than $ y $. For $ y = x ^ {1/ \xi } $ and $ \xi = \xi ( x) \rightarrow \infty $ as $ x \rightarrow \infty $, such numbers are called quasi-prime numbers. By applying the sieve method to these numbers there arose a fairly complete theory of their distribution, similar to that expected from the distribution of prime numbers. The distribution of numbers with small prime divisors has also been considered (see [15]).
References
| [1] | L. Euler, "Einleitung in die Analysis des Unendlichen" , Springer (1983) (Translated from Latin) |
| [2] | P.L. Chebyshev, "Oeuvres de P.L. Tchebycheff" , 1–2 , Chelsea (1961) (Translated from Russian) |
| [3] | B. Riemann, "Werke" , Teubner (1892) |
| [4] | A.E. Ingham, "The distribution of prime numbers" , Cambridge Univ. Press (1932) |
| [5] | A.I. Vinogradov, "Selected works" , Springer (1985) (Translated from Russian) |
| [6] | I.M. Vinogradov, "A new estimate of the function  " Izv. Akad. Nauk SSSR Ser. Mat. , 22 : 2 (1958) pp. 161–164 (In Russian) " Izv. Akad. Nauk SSSR Ser. Mat. , 22 : 2 (1958) pp. 161–164 (In Russian) |
| [7] | I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian) |
| [8] | E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951) |
| [9] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
| [10] | A.A. Karatsuba, "Fundamentals of analytic number theory" , Moscow (1975) (In Russian) |
| [11] | L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen , 1 : 2 (1959) (Heft 13, Teil 1) |
| [12] | N.G. Chudakov, "Introductions to the theory of Dirichlet 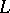 -functions" , Moscow-Leningrad (1947) (In Russian) -functions" , Moscow-Leningrad (1947) (In Russian) |
| [13] | A.F. Lavrik, "On the distribution of primes based on I.M. Vinogradov's method of trigonometric sums" Trudy Mat. Inst. Steklov. , 64 (1961) pp. 90–125 (In Russian) |
| [14] | H. Davenport, "Multiplicative number theory" , Springer (1980) |
| [15] | H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974) |
| [16] | A. Selberg, "An elementary proof of the prime-number theorem" Ann. of Math. , 50 (1949) pp. 305–313 |
| [17] | P. Erdös, "On a new method in elementary number theory which leads to an elementary proof of the prime number theorem" Proc. Nat. Acad. Sci. USA , 35 (1949) pp. 374–384 |
| [18] | A.F. Lavrik, "Survey address" , Internat. Conf. on Number Theory , Moscow (1981) (In Russian) |
| [19] | H.G. Diamond, J. Steinig, "An elementary proof of the prime number theorem with a remainder term" Indag. Math. , 11 (1970) pp. 199–258 |
| [20] | A.F. Lavrik, A.Sh. Sobirov, "On the remainder term in the elementary proof of the prime number theorem" Soviet Math. Dokl. , 211 (1973) pp. 1063–1066 Dokl. Akad. Nauk SSSR , 211 : 3 (1973) pp. 534–536 |
| [21] | B. Rosser, "The  -th prime is greater than -th prime is greater than  " Proc. London Math. Soc. (2) , 45 (1939) pp. 21–44 " Proc. London Math. Soc. (2) , 45 (1939) pp. 21–44 |
| [22] | Yu.V. Linnik, "The large sieve" Dokl. Akad. Nauk SSSR , 30 : 4 (1941) pp. 292–294 (In Russian) |
| [23] | Yu.V. Linnik, "On the least prime in an arithmetic progression I. The basic theorem" Mat. Sb. , 15 (1944) pp. 139–178 (In Russian) |
| [24] | A.F. Lavrik, "A survey of Linnik's large sieve and the density theory of zeros of 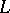 -functions" Russian Math. Surveys , 15 : 2 (1980) pp. 63–76 Uspekhi Mat. Nauk , 35 : 2 (1980) pp. 55–65 -functions" Russian Math. Surveys , 15 : 2 (1980) pp. 63–76 Uspekhi Mat. Nauk , 35 : 2 (1980) pp. 55–65 |
Comments
In formula (7) above, $ \Lambda ( n) $ is the (von) Mangoldt function, which has the value $ \mathop{\rm log} p $ if $ n $ is a prime power $ p ^ {m} $ and is zero otherwise.
Concerning estimates of trigonometric sums see also Trigonometric sums, method of.
Some more facts. Although numerical tables do not suggest it, the function $ \pi ( x) - \mathop{\rm li} ( x) $ changes sign infinitely often. This was shown by Littlewood. By the work of H. Iwaniec, J. Pintz and C.J. Mozzochi it is now (1986) known that $ d _ {n} \ll p _ {n} ^ \theta $ with $ \theta = 11/12 - 1/384 $. The largest known prime twin is $ 1639494 ( 2 ^ {4423} - 1) \pm 1 $( W. Keller, 1983).
Many interesting facts, both computationally and theoretically, on the distribution of primes can be found in [a5], which is written in an elementary style. For elementary methods one can also consult [a1]. In [a4] one finds a simple proof of the prime number theorem.
The fact that there are infinitely many primes (i.e. $ \pi ( x) \rightarrow \infty $ as $ x \rightarrow \infty $) is also known as the Euclidean prime number theorem. The prime number theorem states that $ \pi ( x) $ is asymptotically equal to $ x ( \mathop{\rm log} x) ^ {-} 1 $( cf. also de la Vallée-Poussin theorem). The Dirichlet prime number theorem states that there are infinitely many primes in every arithmetic progression (i.e. $ \pi ( x; d, l) \rightarrow \infty $ as $ x \rightarrow \infty $).
For the result of Bombieri–Vinogradov see also (the references to) Density hypothesis.
References
| [a1] | H.G. Diamond, "Elementary methods in the study of the distribution of prime numbers" Bull. Amer. Math. Soc. , 7 (1982) pp. 553–589 |
| [a2] | W.J. Ellison, M. Mendès France, "Les nombres premiers" , Hermann (1975) |
| [a3] | A. Ivic, "The Riemann zeta-function" , Wiley (1985) |
| [a4] | D.J. Newman, "Simple analytic proof of the prime number theorem" Amer. Math. Monthly , 87 (1980) pp. 693–696 |
| [a5] | H. Riesel, "Prime numbers and computer methods for factorisation" , Birkhäuser (1985) |
| [a6] | E. Bombieri, "La grand crible dans la théorie analytique des nombres" Astérisque , 18 (1974) |
Distribution of prime numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Distribution_of_prime_numbers&oldid=36164