Distribution of power residues and non-residues

The distribution among the numbers 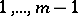of those values of for which the congruence

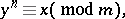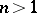, is solvable (or unsolvable) in integers. Questions on the distribution of power residues and non-residues have been studied most fully in the case modulo a prime number 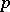. Let 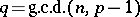. Then the congruence 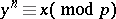is solvable for 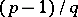values of in the set 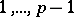and unsolvable for the remaining 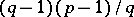values (see Two-term congruence). However, comparatively little is known about how these values are distributed among the numbers .

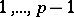The first results about the distribution of power residues were obtained by C.F. Gauss (see [1]) in 1796. From that time until the work of I.M. Vinogradov only isolated special results were obtained on questions concerning the distribution of power residues and non-residues. In 1915, Vinogradov (see [2]) proved a series of general results about the distribution of power residues and non-residues, and about primitive roots (cf. Primitive root) modulo 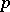among the numbers 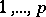. In particular, he obtained the bound

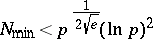for the least quadratic non-residue 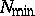, and the bound

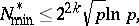where 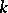is the number of distinct prime divisors of 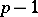, for the least primitive root 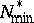modulo .

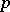In addition, he made a number of conjectures on the distribution of quadratic residues and non-residues (see Vinogradov hypotheses) which stimulated a series of investigations in this area. Thus, Yu.V. Linnik [3] proved that for sufficiently large 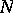, the number of prime numbers 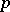in the interval 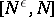for which 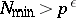does not exceed a certain constant 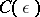, depending only on 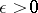. Thus, the prime numbers 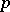for which 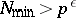, if they exist at all, are met only very rarely. Another significant step in the work on Vinogradov's conjectures was the theorem of D.A. Burgess [4]: For any fixed sufficiently small , the maximal distance 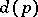between neighbouring quadratic non-residues satisfies the inequality

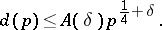In particular, one has

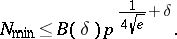In these inequalities, the constants 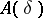, 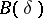depend only on and not on . The proof of Burgess' theorem is very complicated; it is based on the Hasse–Weil theorem on the number of solutions of the hyper-elliptic congruence

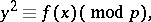the proof of which requires techniques of abstract algebraic geometry. For a simple account of Burgess' theorem see [5], [6].

References

[1]	C.F. Gauss, "Untersuchungen über höhere Arithmetik" , A. Maser (1889) (Translated from Latin)
[2]	I.M. Vinogradov, "Selected works" , Springer (1985) (Translated from Russian)
[3]	Yu.V. Linnik, Dokl. Akad. Nauk SSSR , 36 (1942) pp. 131
[4]	D.A. Burgess, "The distribution of quadratic residues and non-residues" Mathematika , 4 : 8 (1957) pp. 106–112
[5]	S.A. Stepanov, "Constructive methods in the theory of equations over finite fields" Proc. Steklov Inst. Math. , 132 (1975) pp. 271–281 Trudy Mat. Inst. Steklov. , 132 (1973) pp. 237–246
[6]	A.A. Karatsuba, "Character sums and primitive roots in finite fields" Soviet Math.-Dokl. , 9 : 3 (1968) pp. 755–757 Dokl. Akad. Nauk SSSR , 180 : 6 (1968) pp. 1287–1289