Difference between revisions of "Distribution function"
(→References: Feller: internal link) |
(refs format) |
||
| Line 68: | Line 68: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|C}}|| H. Cramér, "Random variables and probability distributions", Cambridge Univ. Press (1970) {{MR|0254895}} {{ZBL|0184.40101}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|C2}}|| H. Cramér, "Mathematical methods of statistics", Princeton Univ. Press (1946) {{MR|0016588}} {{ZBL|0063.01014}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|F}}|| W. Feller, [[Feller, "An introduction to probability theory and its applications"|"An introduction to probability theory and its applications"]], '''1–2''', Wiley (1957–1971) | ||
| + | |- | ||
| + | |valign="top"|{{Ref|BS}}|| L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics", ''Libr. math. tables'', '''46''', Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) {{MR|}} {{ZBL|0529.62099}} | ||
| + | |} | ||
====Comments==== | ====Comments==== | ||
| Line 80: | Line 88: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|JK}}|| N.L. Johnson, S. Kotz, "Distributions in statistics" , Houghton Mifflin (1970) {{MR|0270476}} {{MR|0270475}} {{ZBL|0213.21101}} | ||
| + | |} | ||
Revision as of 17:48, 11 May 2012
of a random variable 
2020 Mathematics Subject Classification: Primary: 60E05 [MSN][ZBL]
The function of a real variable  taking at each
taking at each  the value equal to the probability of the inequality
the value equal to the probability of the inequality  .
.
Every distribution function  has the following properties:
has the following properties:
1)  when
when  ;
;
2)  is left-continuous at every
is left-continuous at every  ;
;
3)  ,
, 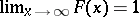 . (Sometimes a distribution function is defined as the probability of
. (Sometimes a distribution function is defined as the probability of 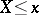 ; it is then right-continuous.)
; it is then right-continuous.)
In mathematical analysis, a distribution function is any function satisfying 1)–3). There is a one-to-one correspondence between the probability distributions  on the
on the 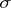 -algebra
-algebra 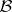 of Borel subsets of the real line
of Borel subsets of the real line 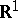 and the distribution functions. This correspondence is as follows: For any interval
and the distribution functions. This correspondence is as follows: For any interval 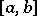 ,
,
 |
Any function  satisfying 1)–3) can be regarded as the distribution function of some random variable
satisfying 1)–3) can be regarded as the distribution function of some random variable 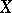 (e.g.
(e.g. 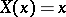 ) defined on the probability space
) defined on the probability space 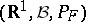 .
.
Any distribution function can be uniquely written as a sum
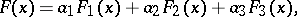 |
where 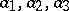 are non-negative numbers with sum equal to 1, and
are non-negative numbers with sum equal to 1, and 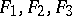 are distribution functions such that
are distribution functions such that 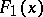 is absolutely continuous,
is absolutely continuous,
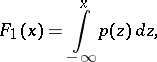 |
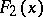 is a "step-function" ,
is a "step-function" ,
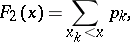 |
where the 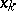 are the points where
are the points where 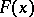 "jumps" and the
"jumps" and the 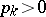 are proportional to the size of these jumps, and
are proportional to the size of these jumps, and 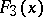 is the "singular" component — a continuous function whose derivative is zero almost-everywhere.
is the "singular" component — a continuous function whose derivative is zero almost-everywhere.
Example. Let  ,
, 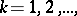 be an infinite sequence of independent random variables assuming the values 1 and 0 with probabilities
be an infinite sequence of independent random variables assuming the values 1 and 0 with probabilities 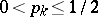 and
and 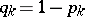 , respectively. Also, let
, respectively. Also, let
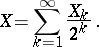 |
Now:
1) if 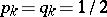 for all
for all 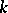 , then
, then 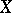 has an absolutely-continuous distribution function (with
has an absolutely-continuous distribution function (with 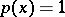 for
for  , that is,
, that is,  is uniformly distributed on
is uniformly distributed on 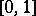 );
);
2) if 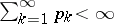 , then
, then  has a "step" distribution function (it has jumps at all the dyadic-rational points in
has a "step" distribution function (it has jumps at all the dyadic-rational points in 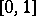 );
);
3) if 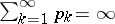 and
and 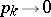 as
as 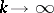 , then
, then 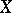 has a "singular" distribution function.
has a "singular" distribution function.
This example serves to illustrate the theorem of P. Lévy asserting that the limit of an infinite convolution of discrete distribution functions can contain only one of the components mentioned above.
The "distance" between two distributions 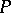 and
and 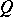 on the real line is often defined in terms of the corresponding distribution functions
on the real line is often defined in terms of the corresponding distribution functions 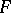 and
and 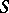 , by putting, for example,
, by putting, for example,
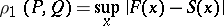 |
or
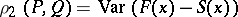 |
(see Distributions, convergence of; Lévy metric; Characteristic function).
The distribution functions of the probability distributions most often used (e.g. the normal, binomial and Poisson distributions) have been tabulated.
To test hypotheses concerning a distribution function 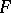 using results of independent observations, one can use some measure of the deviation of
using results of independent observations, one can use some measure of the deviation of 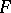 from the empirical distribution function (see Kolmogorov test; Kolmogorov–Smirnov test; Cramér–von Mises test).
from the empirical distribution function (see Kolmogorov test; Kolmogorov–Smirnov test; Cramér–von Mises test).
The concept of a distribution function can be extended in a natural way to the multi-dimensional case, but multi-dimensional distribution functions are significantly less used in comparison to one-dimensional distribution functions.
For a more detailed treatment of distribution functions see Gram–Charlier series; Edgeworth series; Limit theorems.
References
| [C] | H. Cramér, "Random variables and probability distributions", Cambridge Univ. Press (1970) MR0254895 Zbl 0184.40101 |
| [C2] | H. Cramér, "Mathematical methods of statistics", Princeton Univ. Press (1946) MR0016588 Zbl 0063.01014 |
| [F] | W. Feller, "An introduction to probability theory and its applications", 1–2, Wiley (1957–1971) |
| [BS] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics", Libr. math. tables, 46, Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) Zbl 0529.62099 |
Comments
In the Russian literature distributions functions are taken to be left-continuous. In the Western literature it is common to define them to be right-continuous. Thus, the distribution function of a random variable 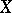 is the function
is the function 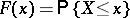 . It then has the properties 1); 2')
. It then has the properties 1); 2') 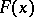 is right-continuous at every
is right-continuous at every  ; 3). The unique probability distribution
; 3). The unique probability distribution 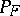 corresponding to it is now defined as
corresponding to it is now defined as
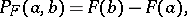 |
while the "step-function" 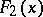 in the above-mentioned decomposition
in the above-mentioned decomposition  is
is
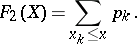 |
References
| [JK] | N.L. Johnson, S. Kotz, "Distributions in statistics" , Houghton Mifflin (1970) MR0270476 MR0270475 Zbl 0213.21101 |
Distribution function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Distribution_function&oldid=26407