Dissipative operator
A linear operator 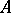 defined on a domain
defined on a domain 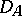 which is dense in a Hilbert space
which is dense in a Hilbert space 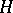 such that
such that
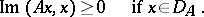 |
This requirement is sometimes replaced by the condition 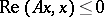 if
if 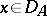 , i.e. the dissipativeness of
, i.e. the dissipativeness of 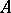 in this sense is equivalent to that of the operator
in this sense is equivalent to that of the operator 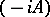 .
.
A dissipative operator is said to be maximal if it has no proper dissipative extensions. A dissipative operator always has a closure, which also is a dissipative operator; in particular, a maximal dissipative operator is a closed operator. Any dissipative operator can be extended to a maximal dissipative operator. For a dissipative operator all points 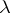 with
with 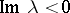 belong to the resolvent set, and moreover
belong to the resolvent set, and moreover
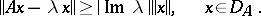 |
A dissipative operator is maximal if and only if 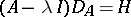 for all
for all 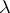 with
with 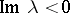 . An equivalent condition for maximality of a dissipative operator is that it is closed and that
. An equivalent condition for maximality of a dissipative operator is that it is closed and that
 |
If  is a maximal symmetric operator, then either
is a maximal symmetric operator, then either 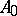 or
or 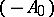 is a maximal dissipative operator. Dissipative and, in particular, maximal dissipative extensions may be considered for an arbitrary symmetric operator
is a maximal dissipative operator. Dissipative and, in particular, maximal dissipative extensions may be considered for an arbitrary symmetric operator 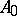 ; their description is equivalent to the description of all maximal dissipative extensions of the conservative operator
; their description is equivalent to the description of all maximal dissipative extensions of the conservative operator 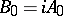 :
:  ,
, 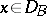 .
.
Dissipative operators are closely connected with contractions (cf. Contraction) and with the so-called accretive operators, i.e. operators 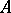 for which
for which 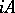 is a dissipative operator. In particular, an accretive operator
is a dissipative operator. In particular, an accretive operator 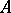 is maximal if and only if
is maximal if and only if 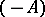 is the generating operator (or generator) of a continuous one-parameter contraction semi-group
is the generating operator (or generator) of a continuous one-parameter contraction semi-group 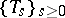 on
on 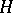 . The Cayley transform
. The Cayley transform
 |
where 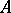 is a maximal accretive operator and
is a maximal accretive operator and  is a contraction not having
is a contraction not having 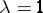 as an eigen value, is used to construct the functional calculus and, in particular, the theory of fractional powers of maximal dissipative operators.
as an eigen value, is used to construct the functional calculus and, in particular, the theory of fractional powers of maximal dissipative operators.
In the case of bounded linear operators 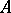 the definition of a dissipative operator is equivalent to the requirement
the definition of a dissipative operator is equivalent to the requirement 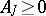 , where
, where 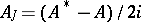 is the imaginary part of the operator
is the imaginary part of the operator 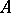 . For a completely-continuous dissipative operator
. For a completely-continuous dissipative operator 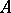 on a separable Hilbert space
on a separable Hilbert space 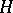 with nuclear imaginary part
with nuclear imaginary part 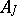 , several criteria (i.e. necessary and sufficient conditions) for the completeness of the system of its root vectors are available; for example,
, several criteria (i.e. necessary and sufficient conditions) for the completeness of the system of its root vectors are available; for example,
 |
where 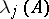 are all eigen values of the operator
are all eigen values of the operator 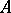 ,
, 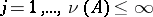 , and
, and 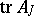 is the trace of the operator
is the trace of the operator 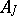 (Livshits' criterion);
(Livshits' criterion);
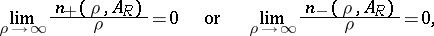 |
where 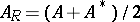 is the real part of
is the real part of 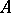 , and
, and 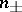 is the number of characteristic numbers of the operator
is the number of characteristic numbers of the operator 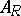 in the segment
in the segment 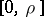 and
and  (Krein's criterion). The system
(Krein's criterion). The system 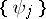 of eigen vectors corresponding to different eigen values
of eigen vectors corresponding to different eigen values 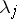 ,
, 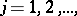 of a dissipative operator forms a basis of its closed linear span and is equivalent to an orthonormal basis if
of a dissipative operator forms a basis of its closed linear span and is equivalent to an orthonormal basis if
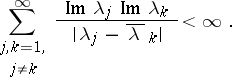 |
The concept of a dissipative operator was also introduced for non-linear and even for multi-valued operators  . Such an operator on a Hilbert space is called dissipative if for any two of its values the inequality
. Such an operator on a Hilbert space is called dissipative if for any two of its values the inequality
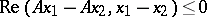 |
holds. This concept also forms the base of the theory of one-parameter non-linear contraction semi-groups and the related differential equations. Another generalization of the concept of a dissipative operator concerns operators acting on a Banach space with a so-called semi-inner product. Another generalization concerns operators acting on a Hilbert space with an indefinite metric.
References
| [1] | B. Szökefalvi-Nagy, Ch. Foiaş, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970) (Translated from French) |
| [2] | S.G. Krein, "Linear differential equations in Banach space" , Transl. Math. Monogr. , 29 , Amer. Math. Soc. (1971) (Translated from Russian) |
| [3] | M.S. Livshits, "On the spectral resolution of linear non-selfadjoint operators" Transl. Amer. Math. Soc. (2) , 5 (1957) pp. 67–114 Mat. Sb. , 34 : 1 (1954) pp. 145–199 |
| [4] | R.S. Phillips, "Dissipative operators and hyperbolic systems of partial differential equations" Trans. Amer. Math. Soc. , 90 : 2 (1959) pp. 193–254 |
| [5] | M. Crandall, A. Pazy, "Semi-groups of nonlinear contractions" J. Funct. Anal. , 3 (1969) pp. 376–418 |
| [6] | G. Lumer, R. Phillips, "Dissipative operators in a Banach space" Pacific J. Math. , 11 (1961) pp. 679–698 |
Comments
A good reference for dissipative operators on more general spaces than Hilbert spaces is [a1]. For operators on Hilbert spaces see also [a2].
References
| [a1] | H.O. Fattorini, "The Cauchy problem" , Addison-Wesley (1983) pp. 120–125; 154–159 |
| [a2] | I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Introduction to the theory of linear nonselfadjoint operators" , Transl. Math. Monogr. , 18 , Amer. Math. Soc. (1969) (Translated from Russian) |
Dissipative operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dissipative_operator&oldid=18700