Discrete topology
on a set 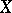
The topology in which every set is open (and therefore every set is closed). The discrete topology is the largest element in the lattice of all topologies on the given set. The term "discrete topology" is sometimes understood in a somewhat wider sense, viz. as a topology in which intersections of arbitrary numbers of open sets are open. In the case of 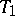 -spaces, both definitions coincide. In this sense, the theory of discrete spaces is equivalent to the theory of partially ordered sets.
-spaces, both definitions coincide. In this sense, the theory of discrete spaces is equivalent to the theory of partially ordered sets.
References
| [1] | P.S. Aleksandrov, "Diskrete Räume" Mat. Sb. , 2 (1937) pp. 501–520 |
Comments
The equivalence alluded to above is obtained as follows: If 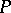 is a pre-ordered set (cf. Pre-order), then define
is a pre-ordered set (cf. Pre-order), then define 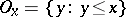 for
for 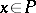 . With the topology generated by the sets
. With the topology generated by the sets 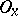 ,
, 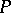 becomes a discrete space.
becomes a discrete space.
If 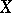 is a discrete space, put
is a discrete space, put 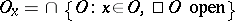 for
for 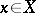 . Then
. Then 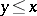 if and only if
if and only if 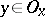 , defines a pre-order on
, defines a pre-order on 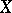 .
.
These constructions are each others inverses. Moreover, discrete 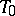 -spaces correspond to partial orders and "real" discrete spaces correspond to discrete orders.
-spaces correspond to partial orders and "real" discrete spaces correspond to discrete orders.
This simple idea and variations thereof have proven to be extremely fruitful, see, e.g., [a1].
References
| [a1] | G. Gierz, K.H. Hofmann, K. Keimel, J.D. Lawson, M.V. Mislove, D.S. Scott, "A compendium of continuous lattices" , Springer (1980) |
Discrete topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Discrete_topology&oldid=11525