Disc of convergence
of a power series
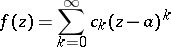 |
The disc 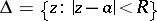 ,
, 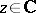 , in which the series
, in which the series
is absolutely convergent, while outside the disc (for 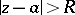 ) it is divergent. In other words, the disc of convergence
) it is divergent. In other words, the disc of convergence 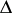 is the interior of the set of points of convergence of the series . Its radius
is the interior of the set of points of convergence of the series . Its radius 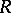 is called the radius of convergence of the series. The disc of convergence may shrink to the point
is called the radius of convergence of the series. The disc of convergence may shrink to the point  when
when  , and it may be the entire open plane, when
, and it may be the entire open plane, when 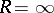 . The radius of convergence
. The radius of convergence 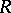 is equal to the distance of the centre
is equal to the distance of the centre  to the set of singular points of
to the set of singular points of 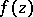 (for the determination of
(for the determination of 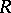 in terms of the coefficients
in terms of the coefficients 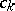 of the series see Cauchy–Hadamard theorem). Any disc
of the series see Cauchy–Hadamard theorem). Any disc 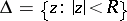 ,
, 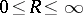 , in the
, in the  -plane is the disc of convergence of some power series.
-plane is the disc of convergence of some power series.
For a power series
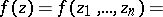 | (2) |
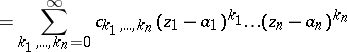 |
in several complex variables  ,
, 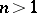 , a polydisc of convergence of the series (2) is defined to be any polydisc
, a polydisc of convergence of the series (2) is defined to be any polydisc
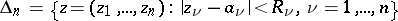 |
at all points of which the series (2) is absolutely convergent, while in any polydisc
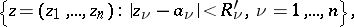 |
where 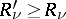 and at least one of the latter inequalities is strict, there is at least one point at which the series is divergent. The radii
and at least one of the latter inequalities is strict, there is at least one point at which the series is divergent. The radii 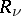 ,
, 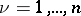 ,
, 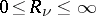 , of the polydisc of convergence are called the associated radii of convergence of the series (2). They are in a well-defined relationship with the coefficients of the series, so that any polydisc with centre
, of the polydisc of convergence are called the associated radii of convergence of the series (2). They are in a well-defined relationship with the coefficients of the series, so that any polydisc with centre  and with radii satisfying this relationship is the polydisc of convergence of a series (2) (cf. Cauchy–Hadamard theorem). Any polydisc
and with radii satisfying this relationship is the polydisc of convergence of a series (2) (cf. Cauchy–Hadamard theorem). Any polydisc 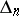 ,
, 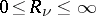 ,
, 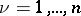 , in the complex space
, in the complex space 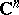 is the polydisc of convergence for some power series in
is the polydisc of convergence for some power series in  complex variables. When
complex variables. When 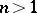 the interior of the set of points of absolute convergence of a series (2) is more complicated — it is a logarithmically convex complete Reinhardt domain with centre
the interior of the set of points of absolute convergence of a series (2) is more complicated — it is a logarithmically convex complete Reinhardt domain with centre  in
in 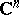 (cf. Reinhardt domain).
(cf. Reinhardt domain).
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1 , Moscow (1976) (In Russian) |
Comments
References
| [a1] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) pp. Chapt. 2.4 |
| [a2] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1978) |
| [a3] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1987) pp. 24 |
Disc of convergence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Disc_of_convergence&oldid=17451