Direction field
A geometrical interpretation of the set of line elements corresponding to a system of ordinary differential equations
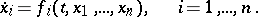 | (1) |
A line element is defined as a sequence of numbers
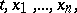 | (2) |
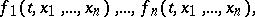 |
where  is a point of the domain
is a point of the domain  , at which the terms on the right-hand side of (1) are defined. A line element (2) can be described as a point
, at which the terms on the right-hand side of (1) are defined. A line element (2) can be described as a point  together with the direction with direction cosines
together with the direction with direction cosines
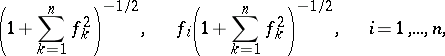 | (3) |
which is represented by a short segment through the point, parallel to the vector
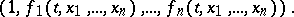 |
For a system in symmetric form,
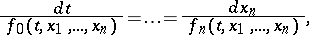 |
unlike system (1), the field may also contain directions orthogonal to the 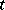 -axis.
-axis.
Consider any integral curve of the system (1). At every point of this curve, the direction field corresponding to the point is tangent to the curve at that point; any curve with this property is an integral curve of (1). Thus, the specification of a direction field is equivalent to the specification of the system (1), and the problem of integrating this system amounts to the determination of the curves in 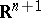 the tangents of which at each point possess the directions defined by the formulas (3), i.e. the directions coinciding with the directions of the field at that point.
the tangents of which at each point possess the directions defined by the formulas (3), i.e. the directions coinciding with the directions of the field at that point.
The geometrical interpretation is particularly easy to visualize when 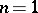 . In that case, for each point
. In that case, for each point 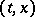 of the domain of definition
of the domain of definition 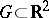 of the right-hand side in the first-order equation
of the right-hand side in the first-order equation
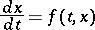 | (4) |
there exists a short segment through the point, with slope  , such that the (directed) angle between the
, such that the (directed) angle between the 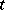 -axis and the segment is equal to
-axis and the segment is equal to 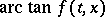 (see Fig.).
(see Fig.).

Figure: d032780a
Frequently, one considers equation (4) together with the differential equation
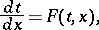 | (5) |
where  for points
for points  at which
at which 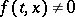 , defining
, defining 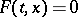 for
for 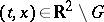 , provided this definition preserves the continuity of
, provided this definition preserves the continuity of 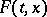 . By this device, the domain
. By this device, the domain 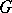 for the pair of equations (4), (5) is extended to a domain
for the pair of equations (4), (5) is extended to a domain  by the addition of the points at which the direction is parallel to the
by the addition of the points at which the direction is parallel to the  -axis, and the integral curves are also allowed to have points with vertical tangents.
-axis, and the integral curves are also allowed to have points with vertical tangents.
If the direction field is drawn in sufficient detail in 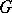 for equation (4) (or in
for equation (4) (or in  for the pair of equations (4), (5)), the pattern of line segments will provide a rough qualitative idea of the behaviour of the integral curves. This idea is the basis for the approximate graphical method for solving equation (4), known as the method of isoclines, in which the direction field is constructed with the aid of isoclines (cf. Isocline). The geometrical relationship between the direction field and the integral curves is also the basis for an approximate numerical method for solving equation (4) — the Euler method.
for the pair of equations (4), (5)), the pattern of line segments will provide a rough qualitative idea of the behaviour of the integral curves. This idea is the basis for the approximate graphical method for solving equation (4), known as the method of isoclines, in which the direction field is constructed with the aid of isoclines (cf. Isocline). The geometrical relationship between the direction field and the integral curves is also the basis for an approximate numerical method for solving equation (4) — the Euler method.
For autonomous systems (cf. Autonomous system) of ordinary differential equations there is a more convenient and intuitive geometrical interpretation in terms of a vector field (cf. also Vector field on a manifold) — the field of phase velocities in the phase space of the system.
References
| [1] | L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian) |
| [2] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1947) |
| [3] | G. Sansone, "Ordinary differential equations" , 1–2 , Zanichelli (1948–1949) (In Italian) |
Comments
The direction field, or line elements field, is often used in textbooks on differential equations in relation with applications in mechanics, biology and econometrics.
Direction field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Direction_field&oldid=12439