Dimension theory
The part of topology in which for every compactum, and subsequently also for more general classes of topological spaces, there is defined in some natural way a numerical topological invariant, the dimension, which coincides if  is a polyhedron (in particular, a manifold) with the number of its coordinates in the sense of elementary or differential geometry. The first general definition of dimension was given by L.E.J. Brouwer (1913) for compacta and even for the wider class of complete metric spaces. The definition is constructed inductively as follows. The empty set is assigned dimension
is a polyhedron (in particular, a manifold) with the number of its coordinates in the sense of elementary or differential geometry. The first general definition of dimension was given by L.E.J. Brouwer (1913) for compacta and even for the wider class of complete metric spaces. The definition is constructed inductively as follows. The empty set is assigned dimension  . Assuming that the spaces of dimension
. Assuming that the spaces of dimension 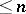 , and hence their subsets, have been defined, one says that a space
, and hence their subsets, have been defined, one says that a space  has dimension
has dimension  if between any two disjoint closed sets
if between any two disjoint closed sets  and
and 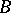 of
of  there is a partition
there is a partition  of dimension
of dimension 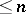 (here a partition between two sets
(here a partition between two sets 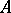 and
and 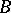 in a space
in a space  is a closed subset
is a closed subset 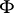 of this space such that the complement
of this space such that the complement 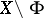 is the sum of two disjoint open sets
is the sum of two disjoint open sets  and
and 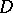 , one of which contains
, one of which contains 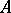 and the other one
and the other one 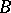 ). In 1921, P.S. Urysohn and K. Menger, independently of Brouwer and each other, arrived at a definition, equivalent in the case of compacta and even of arbitrary separable metric spaces, which differs from Brouwer's definition in that one of the two closed sets
). In 1921, P.S. Urysohn and K. Menger, independently of Brouwer and each other, arrived at a definition, equivalent in the case of compacta and even of arbitrary separable metric spaces, which differs from Brouwer's definition in that one of the two closed sets  ,
, 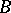 is supposed to consist of one point. The definitions of dimension in the senses of Brouwer and Urysohn–Menger can be formulated for arbitrary Hausdorff spaces. The topological invariants that they define are called the large and the small inductive dimension, respectively, and are denoted by
is supposed to consist of one point. The definitions of dimension in the senses of Brouwer and Urysohn–Menger can be formulated for arbitrary Hausdorff spaces. The topological invariants that they define are called the large and the small inductive dimension, respectively, and are denoted by 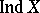 and
and 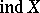 . Always
. Always 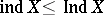 .
.
A completely different approach to the concept of dimension originated from H. Lebesgue, who stated the following theorem: An  -dimensional cube
-dimensional cube 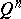 in the sense of elementary geometry can be covered by a finite number of closed sets (even cubes) of diameter
in the sense of elementary geometry can be covered by a finite number of closed sets (even cubes) of diameter 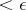 , for any positive number
, for any positive number  , in such a way that the multiplicity (or order) of this covering is
, in such a way that the multiplicity (or order) of this covering is 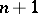 , whereas, for a sufficiently small
, whereas, for a sufficiently small  , there is no covering of
, there is no covering of 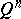 with multiplicity
with multiplicity 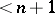 and consisting of closed sets of diameter
and consisting of closed sets of diameter 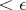 (here the multiplicity of some (finite) collection of sets is the largest integer
(here the multiplicity of some (finite) collection of sets is the largest integer  for which in the given collection there are
for which in the given collection there are 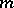 sets with non-empty intersection). Nowadays one can reformulate Lebesgue's theorem as follows: The number of coordinates of the cube
sets with non-empty intersection). Nowadays one can reformulate Lebesgue's theorem as follows: The number of coordinates of the cube 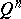 is the smallest integer
is the smallest integer  for which there is an arbitrarily fine (that is, consisting of elements with arbitrarily small diameter) covering of multiplicity
for which there is an arbitrarily fine (that is, consisting of elements with arbitrarily small diameter) covering of multiplicity 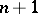 by closed sets. This theorem, proved for the first time by Brouwer, leads to the following definition. The (covering) dimension
by closed sets. This theorem, proved for the first time by Brouwer, leads to the following definition. The (covering) dimension 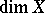 of a compactum
of a compactum 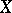 is the smallest number
is the smallest number  such that for any
such that for any  the compactum
the compactum 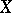 has a covering of multiplicity
has a covering of multiplicity  consisting of closed sets of diameter
consisting of closed sets of diameter  . Without changing the content of this definition, one may replace closed sets by open sets in its formulation.
. Without changing the content of this definition, one may replace closed sets by open sets in its formulation.
When defining the dimension of a compactum 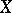 , one uses the notion of the diameter of a set, which is related to the metric, rather than the topology, of
, one uses the notion of the diameter of a set, which is related to the metric, rather than the topology, of  . However, it can be proved that the number
. However, it can be proved that the number 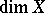 thus defined is nevertheless a topological invariant of
thus defined is nevertheless a topological invariant of 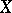 , that is, two homeomorphic compacta have the same dimension. This fact can be established directly, but it is also easily deducible from the fact that
, that is, two homeomorphic compacta have the same dimension. This fact can be established directly, but it is also easily deducible from the fact that  can also be given by a direct topological definition, relying only on the topology of
can also be given by a direct topological definition, relying only on the topology of 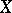 .
.
A covering of a given topological space is any finite collection of open subsets whose union is the whole space. A covering 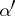 is finer than a covering
is finer than a covering 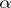 if
if 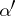 is inscribed in
is inscribed in 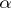 , that is, if each element of
, that is, if each element of 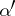 is a subset of at least one element of
is a subset of at least one element of  . It turns out that the dimension
. It turns out that the dimension 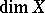 can be defined as follows: The number
can be defined as follows: The number 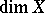 is the smallest integer
is the smallest integer  such that for every covering of
such that for every covering of 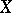 there is a covering of multiplicity
there is a covering of multiplicity 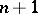 inscribed in it. However, this definition can obviously be formulated not only for compacta, but for arbitrary topological spaces, and makes it possible to define a dimension for them. The dimension
inscribed in it. However, this definition can obviously be formulated not only for compacta, but for arbitrary topological spaces, and makes it possible to define a dimension for them. The dimension 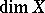 defined in this way for topological spaces enables one to construct a significant theory that is rich in mathematical facts, at least if one stays in the class of normal spaces (and hence, in particular, also metrizable spaces).
defined in this way for topological spaces enables one to construct a significant theory that is rich in mathematical facts, at least if one stays in the class of normal spaces (and hence, in particular, also metrizable spaces).
One of the main problems of dimension theory is the determination of the widest conditions under which the fundamental Urysohn identity holds, namely
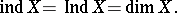 |
It turns out that it holds for all separable metrizable spaces, that is, for all normal spaces with a countable base, and also for the spaces of locally compact Hausdorff groups (Pasynkov's theorem). Without assuming separability, for metrizable spaces one can assert only the validity of the Katětov formula
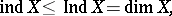 |
and for Hausdorff compacta the Aleksandrov formula
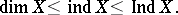 |
There are, however, Hausdorff compacta  for which
for which
 |
(the Lunts–Lokutsievskii example) and Hausdorff compacta  for which
for which
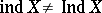 |
(Filippov's example).
The following Nöbeling–Pontryagin theorem is very informative: A necessary and sufficient condition for a topological space 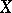 to be homeomorphic to a subspace of a Euclidean space of finite dimension is that
to be homeomorphic to a subspace of a Euclidean space of finite dimension is that 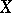 should be a normal space of finite dimension with a countable base. This makes it possible to regard finite-dimensional compacta and, in general, finite-dimensional normal spaces with a countable base as subspaces of Euclidean spaces.
should be a normal space of finite dimension with a countable base. This makes it possible to regard finite-dimensional compacta and, in general, finite-dimensional normal spaces with a countable base as subspaces of Euclidean spaces.
In this connection, the so-called theorem on  -shifts is of particular interest: A compactum
-shifts is of particular interest: A compactum 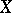 in some Euclidean space
in some Euclidean space 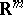 has dimension
has dimension 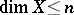 if and only if for any
if and only if for any 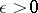 it can be transformed into a polyhedron of dimension
it can be transformed into a polyhedron of dimension 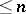 by means of an
by means of an  -shift in the space
-shift in the space 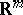 (here an
(here an  -shift of a subspace
-shift of a subspace 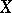 of a Euclidean space
of a Euclidean space 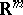 is a continuous mapping
is a continuous mapping  of
of 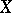 into the Euclidean space
into the Euclidean space 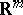 containing it, under which the distance
containing it, under which the distance 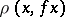 of any point
of any point 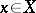 from its image
from its image  is less than
is less than  ). The intuitive meaning of this theorem resides in the fact that every compactum of a given finite dimension
). The intuitive meaning of this theorem resides in the fact that every compactum of a given finite dimension  , regarded as a set in some Euclidean space
, regarded as a set in some Euclidean space 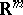 , can by an arbitrarily small modification (which consists of the
, can by an arbitrarily small modification (which consists of the  -shift) be transformed into a polyhedron of the same, but not of smaller, dimension. This theorem, as well as the definition of the dimension
-shift) be transformed into a polyhedron of the same, but not of smaller, dimension. This theorem, as well as the definition of the dimension  for compacta, can be restated in purely topological terms, where again "arbitrarily small" numbers
for compacta, can be restated in purely topological terms, where again "arbitrarily small" numbers 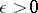 are replaced by "arbitrarily fine" coverings
are replaced by "arbitrarily fine" coverings 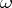 . This makes it possible to formulate an analogous theorem for any normal space, and to arrive at the conclusion that in some (still visualizable) geometrical sense every
. This makes it possible to formulate an analogous theorem for any normal space, and to arrive at the conclusion that in some (still visualizable) geometrical sense every  -dimensional normal space is "similar" and even "differs arbitrarily little from" an
-dimensional normal space is "similar" and even "differs arbitrarily little from" an  -dimensional polyhedron.
-dimensional polyhedron.
One of the main theorems in dimension theory is the so-called theorem on essential mappings, which lies at the foundation of a considerable part of this theory. Let 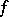 be a continuous mapping from a (normal) space
be a continuous mapping from a (normal) space 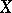 onto an
onto an  -dimensional ball
-dimensional ball  with boundary
with boundary 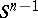 . Let
. Let 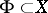 be the pre-image of the sphere
be the pre-image of the sphere 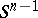 under this mapping,
under this mapping, 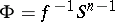 . A mapping
. A mapping 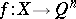 is called essential if every continuous mapping
is called essential if every continuous mapping  that coincides with
that coincides with 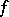 at all points
at all points 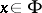 is a mapping onto the whole ball
is a mapping onto the whole ball  . The celebrated Aleksandrov theorem states that a normal space
. The celebrated Aleksandrov theorem states that a normal space 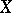 has dimension
has dimension 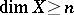 if and only if
if and only if 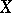 can be essentially mapped onto an
can be essentially mapped onto an  -dimensional ball. From this theorem one can deduce the sum theorem (proved for compacta by Urysohn and Menger already at the very beginning of the development of dimension theory): If a (normal) space
-dimensional ball. From this theorem one can deduce the sum theorem (proved for compacta by Urysohn and Menger already at the very beginning of the development of dimension theory): If a (normal) space 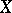 of dimension
of dimension 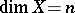 is the union of a finite or countable number of closed subsets
is the union of a finite or countable number of closed subsets 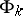 , then for at least one of these
, then for at least one of these  one has
one has 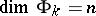 .
.
The theorem on essential mappings lies at the base of so-called homological dimension theory, which makes it possible to apply methods of algebraic topology to the study of dimension under rather general assumptions. The concept of homological dimension of a space is connected with the concepts of a cycle and homology, and hence assumes that alongside with the topological space  one is also given a commutative group
one is also given a commutative group 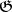 , called the coefficient group. Then one can speak of cycles of the compactum
, called the coefficient group. Then one can speak of cycles of the compactum 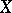 with this coefficient group, of their supports
with this coefficient group, of their supports 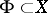 , and, in particular, of cycles homologous to zero in
, and, in particular, of cycles homologous to zero in  for the coefficient domain
for the coefficient domain 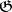 , where these concepts can be equivalently understood both in the sense of the Aleksandrov–Čech homology theory, and in the sense of the Vietoris homology theory.
, where these concepts can be equivalently understood both in the sense of the Aleksandrov–Čech homology theory, and in the sense of the Vietoris homology theory.
After this, one can define the homological dimension of a compactum 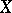 with coefficient group
with coefficient group 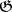 as the largest integer
as the largest integer  for which
for which 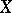 has an
has an  -dimensional cycle
-dimensional cycle 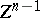 homologous to zero in
homologous to zero in 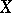 , but not homologous to zero on some support
, but not homologous to zero on some support 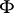 of it. It turns out that if
of it. It turns out that if 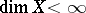 , then
, then 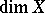 is the homological dimension for the group
is the homological dimension for the group 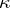 which is the quotient group of the group of all real numbers by the subgroup of integers, and is the largest of all homological dimensions.
which is the quotient group of the group of all real numbers by the subgroup of integers, and is the largest of all homological dimensions.
If from cycles and homology one moves to cocycles and cohomology, then one obtains the cohomological dimension. Moreover, the cohomological dimension of a compactum for a given discrete group 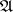 is the homological dimension for the compact Hausdorff group
is the homological dimension for the compact Hausdorff group 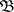 dual to
dual to 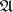 in the sense of Pontryagin's theory of characters. Hence it follows that if
in the sense of Pontryagin's theory of characters. Hence it follows that if 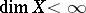 , then
, then 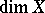 coincides with the cohomological dimension for the group of integers.
coincides with the cohomological dimension for the group of integers.
For references see Dimension.
Comments
The small and large inductive dimensions are usually defined for the classes of regular and normal spaces, respectively. Outside these classes they show pathological behaviour.
Katětov's formula was obtained independently by K. Morita.
Dimension theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dimension_theory&oldid=14136