Dimension
of a topological space 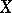
An integral invariant 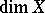 defined as follows.
defined as follows. 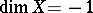 if and only if
if and only if 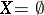 . A non-empty topological space
. A non-empty topological space 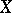 is said to be at most
is said to be at most  -dimensional, written as
-dimensional, written as 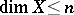 , if in any finite open covering of
, if in any finite open covering of  one can inscribe a finite open covering of
one can inscribe a finite open covering of 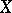 of multiplicity
of multiplicity 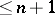 ,
, 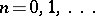 . If
. If 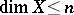 for some
for some 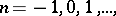 then
then 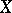 is said to be finite-dimensional, written as
is said to be finite-dimensional, written as  , and one defines
, and one defines
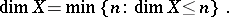 |
Here if 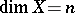 , then the space is called
, then the space is called  -dimensional. The concept of the dimension of a topological space generalizes the elementary geometrical concept of the number of coordinates of a Euclidean space (and a polyhedron), since the dimension of an
-dimensional. The concept of the dimension of a topological space generalizes the elementary geometrical concept of the number of coordinates of a Euclidean space (and a polyhedron), since the dimension of an  -dimensional Euclidean space (and any
-dimensional Euclidean space (and any  -dimensional polyhedron) is equal to
-dimensional polyhedron) is equal to  (the Lebesgue–Brouwer theorem).
(the Lebesgue–Brouwer theorem).
The importance of the concept of the dimension of a topological space is revealed by the Nöbeling–Pontryagin–Hurewicz–Kuratowski theorem: An  -dimensional metrizable space with a countable base can be imbedded in the
-dimensional metrizable space with a countable base can be imbedded in the 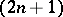 -dimensional Euclidean space. Thus, the class of spaces that are topologically equivalent to subspaces of all possible
-dimensional Euclidean space. Thus, the class of spaces that are topologically equivalent to subspaces of all possible  -dimensional Euclidean spaces,
-dimensional Euclidean spaces, 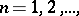 coincides with the class of finite-dimensional metrizable spaces with a countable base.
coincides with the class of finite-dimensional metrizable spaces with a countable base.
The dimension 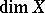 is sometimes called the Lebesgue dimension, since its definition arises from Lebesgue's theorem on tilings: An
is sometimes called the Lebesgue dimension, since its definition arises from Lebesgue's theorem on tilings: An  -dimensional cube has, for any
-dimensional cube has, for any 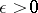 , a finite closed covering of multiplicity
, a finite closed covering of multiplicity 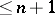 such that all elements have diameter
such that all elements have diameter 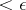 ; there exists an
; there exists an 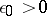 for which the multiplicity of any finite closed covering of an
for which the multiplicity of any finite closed covering of an  -dimensional cube is
-dimensional cube is 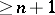 if the diameters of the elements of this covering are
if the diameters of the elements of this covering are 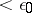 .
.
Another, inductive, approach (see Inductive dimension) to the definition of the dimension of a topological space is possible, based on the separation of the space by subspaces of smaller dimension. This approach to the concept of dimension originates from H. Poincaré, L.E.J. Brouwer, P.S. Urysohn, and K. Menger. In the case of metrizable spaces it is equivalent to Lebesgue's definition.
The foundations of dimension theory were laid in the first half of the twenties of the 20th century in papers of Urysohn and Menger. In the later thirties, the dimension theory of metrizable spaces with a countable base was constructed, and by the start of the sixties the dimension theory of arbitrary metrizable spaces was finished.
Below, all topological spaces under consideration are supposed to be normal and Hausdorff (cf. Hausdorff space; Normal space). In this case, in the definition of dimension one can without harm replace the open coverings to be inscribed by closed ones.
Lebesgue's approach to the definition of dimension (in contrast to the inductive approach) makes it possible to geometrize the concept of dimension for any space by comparing the original topological space with most simple geometrical formations — polyhedra (cf. Polyhedron). Roughly speaking, a space is  -dimensional if and only if it differs arbitrarily little from an
-dimensional if and only if it differs arbitrarily little from an  -dimensional polyhedron. More precisely, there is Aleksandrov's theorem on
-dimensional polyhedron. More precisely, there is Aleksandrov's theorem on 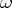 -mappings:
-mappings: 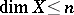 if and only if for any finite open covering
if and only if for any finite open covering 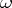 of
of 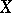 there is an
there is an 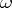 -mapping from
-mapping from 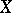 onto an at most
onto an at most  -dimensional,
-dimensional, 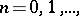 (compact) polyhedron. This theorem can be particularly visualized for compacta: A compactum
(compact) polyhedron. This theorem can be particularly visualized for compacta: A compactum 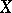 has
has 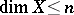 if and only if for any
if and only if for any 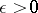 there is an
there is an  -mapping from
-mapping from 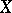 onto an at most
onto an at most  -dimensional polyhedron. If
-dimensional polyhedron. If 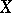 also lies in a Euclidean or Hilbert space, then the
also lies in a Euclidean or Hilbert space, then the  -mapping can be replaced by an
-mapping can be replaced by an  -shift (Aleksandrov's theorem on
-shift (Aleksandrov's theorem on  -mappings and
-mappings and  -shifts).
-shifts).
The following statement makes it possible to determine the dimension of a space by comparing it with all possible  -dimensional cubes:
-dimensional cubes: 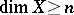 if and only if the space has an essential mapping onto an
if and only if the space has an essential mapping onto an  -dimensional cube,
-dimensional cube, 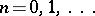 (Aleksandrov's theorem on essential mappings).
(Aleksandrov's theorem on essential mappings).
This theorem can be given the following form:  if and only if, for any set
if and only if, for any set 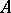 closed in
closed in 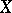 and for any continuous mapping
and for any continuous mapping 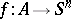 into the
into the  -dimensional sphere, there is a continuous extension
-dimensional sphere, there is a continuous extension 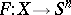 ,
, 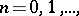 of
of 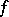 .
.
The following characterization of dimension indicates the role of this concept in problems of the existence of solutions to systems of equations: 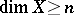 ,
, 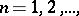 if and only if
if and only if 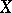 has a system of disjoint pairs of closed sets
has a system of disjoint pairs of closed sets 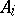 ,
, 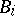 ,
, 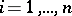 , such that for any functions
, such that for any functions 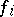 continuous on
continuous on 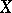 and satisfying the conditions
and satisfying the conditions 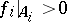 ,
, 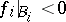 ,
, 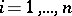 , there is a point
, there is a point 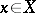 at which
at which 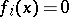 ,
, 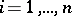 (this is the Otto–Eilenberg–Hemmingsen theorem on partitions).
(this is the Otto–Eilenberg–Hemmingsen theorem on partitions).
One of the most important properties of dimension is expressed by the Menger–Urysohn–Čech countable closed sum theorem: If the space 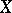 is a finite or countable sum of closed subsets of dimension
is a finite or countable sum of closed subsets of dimension 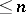 , then also
, then also 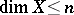 ,
, 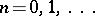 . In this theorem, the condition that the sum be finite or countable may be replaced by the condition of local finiteness. The statement for the large and small inductive dimensions analogous to this sum theorem already fails in the class of Hausdorff compacta. The following statements are among the fundamental general facts of dimension theory, and make it possible to reduce the consideration of arbitrary spaces to that of Hausdorff compacta. For any normal space
. In this theorem, the condition that the sum be finite or countable may be replaced by the condition of local finiteness. The statement for the large and small inductive dimensions analogous to this sum theorem already fails in the class of Hausdorff compacta. The following statements are among the fundamental general facts of dimension theory, and make it possible to reduce the consideration of arbitrary spaces to that of Hausdorff compacta. For any normal space
a) 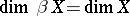 ,
, 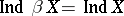 , where
, where 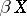 is the Stone–Čech compactification of
is the Stone–Čech compactification of 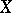 ; at the same time, the inequality
; at the same time, the inequality 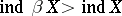 is possible;
is possible;
b) there exists a compactification 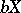 of
of 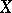 with weight (cf. Weight of a topological space)
with weight (cf. Weight of a topological space) 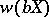 equal to the weight
equal to the weight 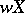 and with dimension
and with dimension 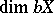 equal to the dimension
equal to the dimension 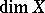 ; the analogous statement also holds for the large inductive dimension. The case of a countable weight of the space is especially interesting, since in this case the extension
; the analogous statement also holds for the large inductive dimension. The case of a countable weight of the space is especially interesting, since in this case the extension 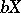 is metrizable.
is metrizable.
Statement b) can be strengthened: For any 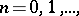 and any infinite cardinal number
and any infinite cardinal number  there is a Hausdorff compactum
there is a Hausdorff compactum 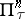 of weight
of weight  and dimension
and dimension 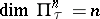 containing a homeomorphic image of every normal space
containing a homeomorphic image of every normal space 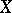 of weight
of weight 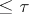 and dimension
and dimension 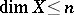 (the theorem on the universal Hausdorff compactum of given weight and dimension). The analogous statement also holds for the large inductive dimension. Here for
(the theorem on the universal Hausdorff compactum of given weight and dimension). The analogous statement also holds for the large inductive dimension. Here for 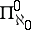 one can take the perfect Cantor set, and as
one can take the perfect Cantor set, and as 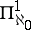 the Menger universal curve.
the Menger universal curve.
It would seem that dimension should possess the monotonicity property: 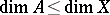 if
if 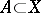 . This is so if a) the set
. This is so if a) the set 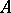 is closed in
is closed in 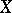 or is strongly paracompact; or b) the space
or is strongly paracompact; or b) the space 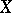 is metrizable (and even perfectly normal). However, already for a subset
is metrizable (and even perfectly normal). However, already for a subset 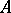 of a hereditarily normal space
of a hereditarily normal space 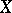 one may have
one may have 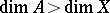 and
and 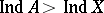 . But always
. But always 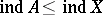 for
for 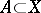 .
.
One of the main problems in dimension theory is the behaviour of dimension under continuous mappings. In the case of closed mappings (these also include all continuous mappings of Hausdorff compacta) the answer is given by the formulas of W. Hurewicz, which he originally obtained for the class of spaces with a countable base.
Hurewicz' formula for mappings raising the dimension: If a mapping 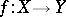 is continuous and closed, then
is continuous and closed, then
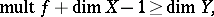 |
where 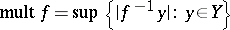 is the multiplicity of
is the multiplicity of 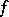 .
.
Hurewicz' formula for mappings lowering the dimension: For a continuous closed mapping 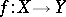 onto a paracompactum
onto a paracompactum 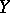 , the inequality
, the inequality
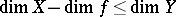 | (1) |
holds, where
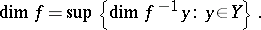 |
For an arbitrary normal space 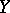 this formula is, in general, false.
this formula is, in general, false.
In the case of continuous mappings of finite-dimensional compacta, it has been established that a continuous mapping 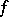 of dimension
of dimension 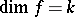 is a superposition of
is a superposition of 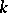 continuous mappings of dimension 1 (this is a precization of formula (1), and an analogue of the fact that a
continuous mappings of dimension 1 (this is a precization of formula (1), and an analogue of the fact that a 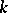 -dimensional cube is the product of
-dimensional cube is the product of 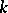 intervals).
intervals).
In the case of open mappings one can show that the image of a zero-dimensional Hausdorff compactum is zero-dimensional and, at the same time, that the Hilbert cube is the image of a one-dimensional compactum, even if the corresponding mapping 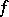 has dimension
has dimension 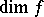 equal to zero. However, in the case of an open mapping
equal to zero. However, in the case of an open mapping 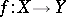 of Hausdorff compacta
of Hausdorff compacta 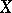 and
and 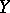 with multiplicity
with multiplicity 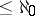 , the equality
, the equality 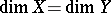 holds.
holds.
The behaviour of dimension under topological products is described by the following assertions:
a) there exist finite-dimensional compacta 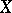 and
and 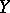 for which
for which 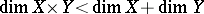 ;
;
b) if one of the factors of the product 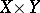 is a Hausdorff compactum or metrizable, then
is a Hausdorff compactum or metrizable, then  ;
;
c) there exist normal spaces 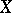 and
and 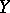 for which
for which 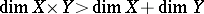 .
.
In the case of Hausdorff compacta 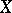 and
and 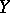 one always has
one always has 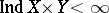 if
if 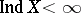 and
and 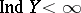 , but one may have
, but one may have 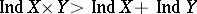 . If, however, the Hausdorff compacta
. If, however, the Hausdorff compacta 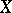 and
and 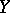 are perfectly normal or one-dimensional, then
are perfectly normal or one-dimensional, then 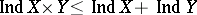 .
.
Dimension theory is most meaningful, first, for the class of metric spaces with a countable base, and, secondly, for the class of all metric spaces. In the class of metric spaces with a countable base one has the Urysohn equalities
 | (2) |
In the class of arbitrary metric spaces one has the Katětov equality
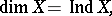 | (3) |
and 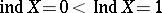 is possible.
is possible.
In the case of metric spaces the concept of an  -dimensional space can be reduced to the concept of a zero-dimensional space by the following two methods. For a metric space
-dimensional space can be reduced to the concept of a zero-dimensional space by the following two methods. For a metric space 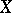 ,
, 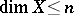 ,
, 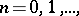 if and only if
if and only if
a) 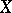 can be represented by at most
can be represented by at most 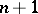 zero-dimensional summands; or
zero-dimensional summands; or
b) there exists a continuous closed mapping of multiplicity 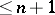 from a zero-dimensional metric space onto
from a zero-dimensional metric space onto  .
.
For any subset 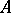 of a metric space
of a metric space 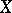 there is a subset
there is a subset 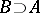 of type
of type 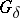 in
in 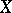 for which
for which 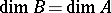 .
.
In the class of metric spaces of weight 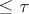 and dimension
and dimension 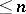 there exists a universal space (in the sense of imbedding). Dowker's theorem has played an important role in the dimension theory of metric (and more general) spaces:
there exists a universal space (in the sense of imbedding). Dowker's theorem has played an important role in the dimension theory of metric (and more general) spaces: 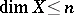 if and only if in any locally finite open covering of
if and only if in any locally finite open covering of 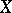 one can inscribe an open covering of multiplicity
one can inscribe an open covering of multiplicity 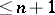 .
.
One of the most important problems in dimension theory is the problem of the relations between the Lebesgue dimension and the inductive dimensions. Although for an arbitrary space 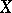 the values of the dimensions
the values of the dimensions 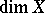 ,
, 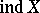 ,
, 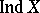 are, in general, pairwise distinct, for some classes of spaces that are in some sense close to metric spaces one has, e.g., the following:
are, in general, pairwise distinct, for some classes of spaces that are in some sense close to metric spaces one has, e.g., the following:
a) if the space 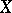 admits a continuous closed mapping
admits a continuous closed mapping 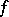 of dimension
of dimension 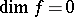 onto a metric space, then (3) holds, whence follow the equalities (2) for locally compact Hausdorff groups and their quotient spaces;
onto a metric space, then (3) holds, whence follow the equalities (2) for locally compact Hausdorff groups and their quotient spaces;
b) if there exists a continuous closed mapping from a metric space onto 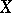 , then (2) holds.
, then (2) holds.
One more general condition for equality (3) to hold for a paracompactum 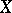 is as follows:
is as follows: 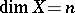 and
and 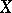 is the image of a zero-dimensional space under a closed mapping of multiplicity
is the image of a zero-dimensional space under a closed mapping of multiplicity 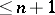 ,
, 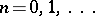 .
.
In the case of an arbitrary space 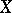 one always has the inequalities
one always has the inequalities 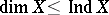 and
and 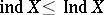 , while the equalities
, while the equalities 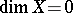 and
and 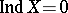 are equivalent. For a strongly paracompact (in particular, for a Hausdorff compact or Lindelöf compact) space
are equivalent. For a strongly paracompact (in particular, for a Hausdorff compact or Lindelöf compact) space 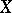 one has the inequality
one has the inequality 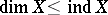 . For Hausdorff compacta the equalities
. For Hausdorff compacta the equalities 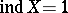 and
and 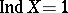 are equivalent. There exist Hausdorff compacta satisfying the first axiom of countability (and even perfectly-normal Hausdorff compacta, if one assumes the continuum hypothesis), for which
are equivalent. There exist Hausdorff compacta satisfying the first axiom of countability (and even perfectly-normal Hausdorff compacta, if one assumes the continuum hypothesis), for which 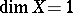 and
and 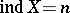 ,
, 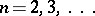 . An example of a topologically homogeneous Hausdorff compactum with
. An example of a topologically homogeneous Hausdorff compactum with 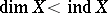 has been constructed. For perfectly-normal Hausdorff compacta one always has
has been constructed. For perfectly-normal Hausdorff compacta one always has 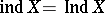 . There exist Hausdorff compacta, satisfying even the first axiom of countability, for which
. There exist Hausdorff compacta, satisfying even the first axiom of countability, for which 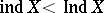 . It is not known (1983) whether there exists an
. It is not known (1983) whether there exists an 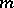 such that for every
such that for every 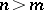 there is a Hausdorff compactum (a metric space)
there is a Hausdorff compactum (a metric space) 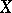 with
with 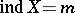 ,
, 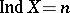 .
.
In the case of non-metrizable spaces, the dimension may not only fail to be monotone, but it also has other pathological properties. For any 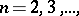 an example of a Hausdorff compactum
an example of a Hausdorff compactum 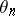 in which any closed set has dimension either 0 or
in which any closed set has dimension either 0 or 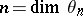 has been constructed. An analogous example for the inductive dimension is impossible. Also, for each
has been constructed. An analogous example for the inductive dimension is impossible. Also, for each 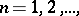 an example of a Hausdorff compactum
an example of a Hausdorff compactum  for which any closed set separating
for which any closed set separating 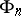 has dimension
has dimension 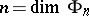 has been constructed. Thus, the approach to the definition of dimension in the case of a non-metrizable space differs in principle from the inductive approach of Poincaré based on the separation of the space by spaces of a smaller number of coordinates. The Hausdorff compacta
has been constructed. Thus, the approach to the definition of dimension in the case of a non-metrizable space differs in principle from the inductive approach of Poincaré based on the separation of the space by spaces of a smaller number of coordinates. The Hausdorff compacta 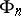 are directly related to the following statement: Any
are directly related to the following statement: Any  -dimensional Hausdorff compactum contains an
-dimensional Hausdorff compactum contains an  -dimensional Cantor manifold.
-dimensional Cantor manifold.
A subset of an  -dimensional Euclidean space
-dimensional Euclidean space 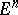 is
is  -dimensional if and only if it contains interior points with respect to
-dimensional if and only if it contains interior points with respect to 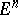 . A compactum has dimension
. A compactum has dimension 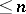 if and only if it has a mapping of dimension zero into
if and only if it has a mapping of dimension zero into 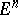 , hence, up to zero-dimensional mappings,
, hence, up to zero-dimensional mappings,  -dimensional compacta are indistinguishable from the bounded closed subsets of
-dimensional compacta are indistinguishable from the bounded closed subsets of 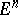 containing interior points (with respect to
containing interior points (with respect to 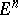 ).
).
See also Dimension theory.
References
| [1] | P.S. Aleksandrov, B.A. Pasynkov, "Introduction to dimension theory" , Moscow (1973) (In Russian) |
| [2] | W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948) |
| [3] | P.S. Urysohn, "Works on topology and other areas of mathematics" , 1–2 , Moscow-Leningrad (1951) (In Russian) |
Comments
Let 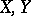 be topological spaces and let
be topological spaces and let 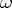 be a covering of
be a covering of 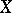 . A continuous mapping
. A continuous mapping 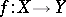 is an
is an 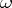 -mapping if each point
-mapping if each point 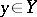 has a neighbourhood
has a neighbourhood 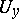 such that
such that 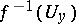 is included in some element of
is included in some element of 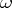 . Let
. Let 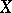 be metric; then
be metric; then 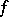 is called an
is called an  -mapping for an
-mapping for an 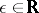 ,
, 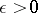 , if the diameter of each
, if the diameter of each 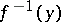 is
is 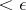 . Finally, a continuous mapping of a subset
. Finally, a continuous mapping of a subset 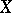 of a Euclidean or Hilbert space
of a Euclidean or Hilbert space  into
into 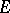 is called an
is called an  -shift if each point of
-shift if each point of 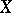 gets displaced at most by
gets displaced at most by  .
.
Lebesgue's theorem on tilings is also called the Lebesgue–Brouwer theorem on tilings or the Pflastersatz.
The Katětov equality (3) is also called the Katetov–Morito equality (of dimensions of metrizable spaces).
The Lebesgue dimension is also called the covering dimension. A metrizable space 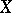 with
with 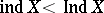 was constructed by P. Roy [a2].
was constructed by P. Roy [a2].
For still other notions of dimension cf. also Fractal dimension and Hausdorff dimension.
References
| [a1] | R. Engelking, "Dimension theory" , North-Holland & PWN (1978) |
| [a2] | P. Roy, "Nonequality of dimensions for metric spaces" Trans. Amer. Math. Soc. , 134 (1968) pp. 117–132 |
| [a3] | J.-I. Nagata, "Modern dimension theory" , Heldermann (1983) |
Dimension of an associative ring.
Comments
A number associated to a ring or module in such a way that its behaviour under some classical operations, e.g. subobjects, quotient objects, direct sums or products, extensions may be studied. It is possible to introduce many different notions of dimension; the success of the theory one can develop depends, however, on the properties with respect to the kind of operations mentioned above, so that good techniques for giving proofs by induction on the dimension become available. Several of the dimensions most used in algebra and ring theory may be defined on the lattice of submodules of some module, globalizing the definition by considering the supremum (or a similar invariant) of the dimension of all modules (perhaps restricting to a certain class of modules). In this way one may define the Goldie dimension, the dual Goldie dimension, the Krull dimension, and the Gabriel dimension, as well as relative versions of these defined by restricting to suitable subcategories of modules. Certain dimensions are defined starting from the principle of resolutions in the category of modules, these dimensions include the homological dimensions, e.g. the projective dimension of a module (or ring), the injective dimension of a module (or ring) and the weak or flat dimensions of a module (cf. also Homological dimension). Many concrete problems concerning rings or modules may be solved by the introduction of the appropriate notion of dimension. As another example one can mention the so-called
may be studied. It is possible to introduce many different notions of dimension; the success of the theory one can develop depends, however, on the properties with respect to the kind of operations mentioned above, so that good techniques for giving proofs by induction on the dimension become available. Several of the dimensions most used in algebra and ring theory may be defined on the lattice of submodules of some module, globalizing the definition by considering the supremum (or a similar invariant) of the dimension of all modules (perhaps restricting to a certain class of modules). In this way one may define the Goldie dimension, the dual Goldie dimension, the Krull dimension, and the Gabriel dimension, as well as relative versions of these defined by restricting to suitable subcategories of modules. Certain dimensions are defined starting from the principle of resolutions in the category of modules, these dimensions include the homological dimensions, e.g. the projective dimension of a module (or ring), the injective dimension of a module (or ring) and the weak or flat dimensions of a module (cf. also Homological dimension). Many concrete problems concerning rings or modules may be solved by the introduction of the appropriate notion of dimension. As another example one can mention the so-called 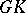 -dimension (Gel'fand–Kirillov) that is related to a notion of a non-commutative transcendence degree and that can be used to obtain information about the imbedding of free algebras in the ring considered, e.g. in certain rings of differential operators (the simplest cases of which are the Weyl algebras. The Weyl algebra
-dimension (Gel'fand–Kirillov) that is related to a notion of a non-commutative transcendence degree and that can be used to obtain information about the imbedding of free algebras in the ring considered, e.g. in certain rings of differential operators (the simplest cases of which are the Weyl algebras. The Weyl algebra 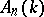 over a field of characteristic zero
over a field of characteristic zero 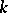 is the algebra
is the algebra 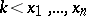 ;
; 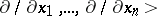 , i.e. the associative algebra generated by
, i.e. the associative algebra generated by 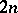 symbols
symbols 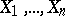 ,
, 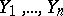 subject to the relations
subject to the relations 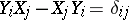 where
where  is the Kronecker symbol).
is the Kronecker symbol).
Below the definitions of those dimensions most commonly used in algebra are give.
Krull dimension. For a partially ordered set 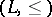 , let
, let 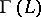 be the set
be the set 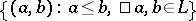 . By transfinite recursion one may define on
. By transfinite recursion one may define on 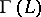 a filtration:
a filtration:
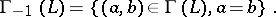 |
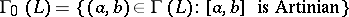 |
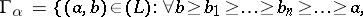 |
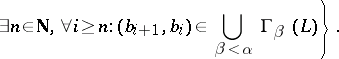 |
In this way one obtains an ascending chain:
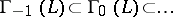 |
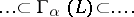 |
Since  is a set it follows that
is a set it follows that 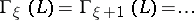 . If
. If 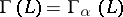 , one says that the Krull dimension
, one says that the Krull dimension 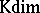 of
of 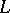 is defined. If
is defined. If 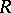 is a ring and
is a ring and 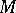 is a left
is a left 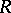 -module, one says that
-module, one says that 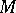 has Krull dimension if the lattice
has Krull dimension if the lattice 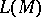 of left submodules of
of left submodules of 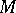 has Krull dimension. If the left
has Krull dimension. If the left 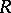 -module
-module 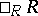 has Krull dimension, one says that the ring
has Krull dimension, one says that the ring 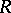 has Krull dimension.
has Krull dimension.
Gabriel dimension. For a modular upper-continuous lattice (cf. Continuous lattice; Modular lattice) 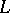 having 0 and 1 one defines
having 0 and 1 one defines 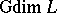 by transfinite recursion.
by transfinite recursion. 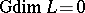 if and only if
if and only if 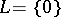 . Let
. Let  be a non-limit ordinal number and assume that the Gabriel dimension
be a non-limit ordinal number and assume that the Gabriel dimension 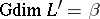 has already been defined for lattices with
has already been defined for lattices with 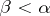 . One says that
. One says that 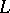 is
is 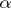 -simple if for each
-simple if for each 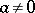 in
in 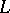 one has:
one has:  is not smaller that
is not smaller that 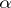 but
but 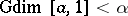 . One says that
. One says that 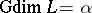 if
if 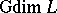 is not smaller than
is not smaller than 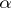 but for every
but for every 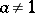 in
in 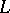 there is some
there is some 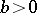 such that
such that 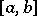 is
is 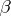 -simple for some
-simple for some 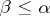 . If
. If 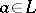 and
and 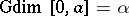 , one says that
, one says that  has Gabriel dimension
has Gabriel dimension 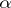 . If
. If 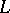 has Krull dimension, then
has Krull dimension, then 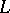 also has Gabriel dimension, and
also has Gabriel dimension, and 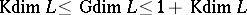 .
.
If 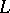 is a Noetherian lattice, then
is a Noetherian lattice, then 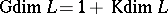 .
.
If 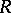 is a ring and
is a ring and 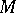 is a left
is a left 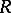 -module, then
-module, then 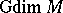 is defined to be
is defined to be 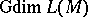 .
.
It is somewhat remarkable that affine PI-rings (cf. PI-algebra) need not have Krull dimension, while on the other hand these rings have finite Gabriel dimensions.
Projective dimension. A projective resolution of a left 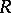 -module
-module  is an exact sequence
is an exact sequence
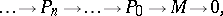 |
where each 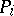 is a projective left
is a projective left 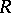 -module (cf. also Resolution). If
-module (cf. also Resolution). If 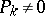 but
but 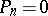 for all
for all 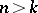 , then one says that the resolution has infinite length. It is easy to prove that each module
, then one says that the resolution has infinite length. It is easy to prove that each module 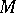 has a projective resolution and so one may define
has a projective resolution and so one may define 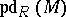 , the projective dimension of
, the projective dimension of 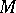 , to be the least
, to be the least  for which
for which 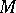 has a projective resolution of length
has a projective resolution of length  . If such an
. If such an  does not exist, one puts
does not exist, one puts 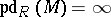 ; clearly,
; clearly, 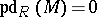 if and only if
if and only if 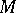 is projective (cf. Projective module). The (left) global dimension
is projective (cf. Projective module). The (left) global dimension 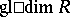 of
of 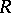 is defined to be
is defined to be 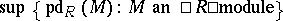 ; in fact, this global dimension is the same if one uses right modules for its determination.
; in fact, this global dimension is the same if one uses right modules for its determination.
One may define the injective dimension of a module 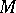 in a completely dual way, using injective resolutions, such that
in a completely dual way, using injective resolutions, such that 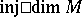 is the length of a minimal injective resolution for
is the length of a minimal injective resolution for 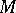 . The global (left) injective dimension of
. The global (left) injective dimension of 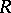 is defined to be the supremum of the injective dimensions of arbitrary (left)
is defined to be the supremum of the injective dimensions of arbitrary (left) 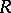 -modules, but one can establish that this dimension of the ring
-modules, but one can establish that this dimension of the ring 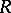 is the same as
is the same as 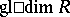 defined as above using projective resolutions.
defined as above using projective resolutions.
Moreover, if 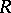 is a left and right Noetherian ring, then the left and right global dimensions of
is a left and right Noetherian ring, then the left and right global dimensions of 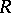 are the same. Note that the semi-simple Artinian rings are characterized by the fact that they have global dimension zero (cf. also Artinian ring).
are the same. Note that the semi-simple Artinian rings are characterized by the fact that they have global dimension zero (cf. also Artinian ring).
Instead of considering projective resolutions one may look at resolutions of 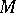 in terms of flat
in terms of flat 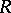 -modules (cf. Flat module). The dimension defined in this way is the flat dimension, or weak dimension, of
-modules (cf. Flat module). The dimension defined in this way is the flat dimension, or weak dimension, of 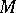 , denoted by
, denoted by 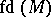 . The left weak dimension
. The left weak dimension 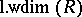 of
of 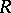 is defined to be
is defined to be 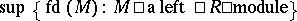 ; the right weak dimension
; the right weak dimension 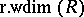 is defined similarly. Cf. also Homological dimension.
is defined similarly. Cf. also Homological dimension.
For a left Noetherian ring 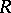 ,
, 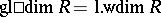 ; for a right Noetherian ring
; for a right Noetherian ring 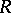 ,
, 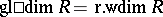 . So for left and right Noetherian rings the projective global dimension, the injective global dimension and the weak dimension coincide; this is not true for arbitrary
. So for left and right Noetherian rings the projective global dimension, the injective global dimension and the weak dimension coincide; this is not true for arbitrary 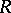 -modules though.
-modules though.
The global dimension is important in the study of commutative regular local rings that play an important part in basic algebraic geometry. Note that a local commutative ring is regular exactly then when it has finite global dimension, and in this case the global dimension equals the Krull dimension.
Gel'fand–Kirillov dimension. For an algebra 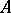 over a field
over a field 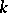 one considers subalgebras
one considers subalgebras 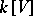 in
in 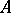 generated over
generated over 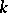 by a vector space
by a vector space 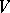 over
over 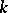 contained in
contained in 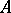 . If
. If 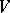 is finite dimensional over
is finite dimensional over 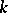 and
and 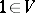 , then
, then 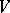 is called a frame for
is called a frame for 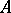 if
if 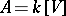 and a subframe otherwise. Let
and a subframe otherwise. Let  be a subframe of
be a subframe of 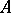 and let
and let 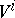 be the set of monomials of length
be the set of monomials of length 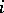 in
in  . Write
. Write 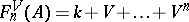 . Then
. Then 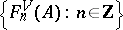 defines a filtration on
defines a filtration on 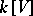 , where by definition
, where by definition 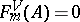 for
for 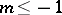 . The associated graded ring of this filtration is isomorphic to
. The associated graded ring of this filtration is isomorphic to 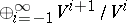 .
.
Define  and
and 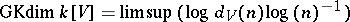 . This number is well-defined and it depends only on
. This number is well-defined and it depends only on 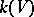 but not on the choice of
but not on the choice of 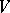 .
.
Put 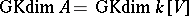 if
if 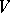 is a frame for
is a frame for 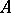 . If
. If 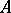 is algebraic over
is algebraic over 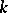 , then
, then  (cf. also Algebraic algebra). Note that
(cf. also Algebraic algebra). Note that  is a real number but not necessarily an integer; W. Borho and H. Kraft have shown that any
is a real number but not necessarily an integer; W. Borho and H. Kraft have shown that any 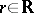 with
with 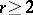 can appear as the GKdim of some
can appear as the GKdim of some 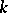 -algebra. In the interval
-algebra. In the interval 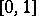 only 0 and 1 can appear as GKdim of a
only 0 and 1 can appear as GKdim of a 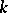 -algebra; G. Bergman proved that numbers in
-algebra; G. Bergman proved that numbers in 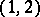 cannot appear as the GKdim of some
cannot appear as the GKdim of some 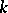 -algebra. That this dimension is sometimes related to the Krull dimension is not a big surprise, at least in the commutative case.
-algebra. That this dimension is sometimes related to the Krull dimension is not a big surprise, at least in the commutative case.
If  is a finitely-generated module over an affine commutative
is a finitely-generated module over an affine commutative 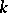 -algebra, then
-algebra, then 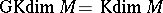 .
.
If 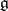 is a solvable Lie algebra over
is a solvable Lie algebra over 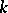 , say
, say 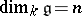 , then the GKdim of the universal enveloping algebra
, then the GKdim of the universal enveloping algebra 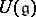 satisfies
satisfies 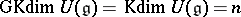 .
.
If 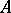 is a prime PI-algebra, then
is a prime PI-algebra, then 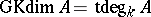 and in the affine case this number also equals the classical Krull dimension,
and in the affine case this number also equals the classical Krull dimension, 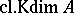 , defined in terms of the length of maximal chains of prime ideals of
, defined in terms of the length of maximal chains of prime ideals of 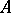 .
.
The Gel'fand–Kirillov transcendence degree 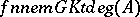 is defined to be
is defined to be 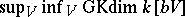 , where
, where 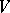 ranges over the subframes of
ranges over the subframes of 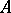 and
and 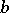 ranges over the regular elements of
ranges over the regular elements of 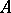 . If
. If 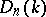 is the
is the  -th Weyl field, the quotient division algebra of
-th Weyl field, the quotient division algebra of 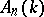 , then
, then 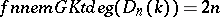 , whereas
, whereas 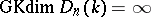 , so the transcendence degree is somewhat better behaved when dealing with rings of differential operators.
, so the transcendence degree is somewhat better behaved when dealing with rings of differential operators.
There are a large number of concepts called "dimension" in many parts of mathematics. The three principal groups appear to be the topological concepts (including the dimension of differentiable and analytic manifolds) and the algebraic ones described above, and the ideas of dimension in algebraic and analytic geometry; cf. also Analytic space; Rational function; Analytic set; Cohomological dimension; Spectrum of a ring. The last group of dimension ideas, i.e. those of algebraic and analytic geometry, are intermediate between the other two and form something of a bridge.
A topological space is irreducible if it can not be written as a union of two proper closed subspaces 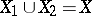 ,
, 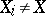 . A topological space
. A topological space 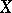 is called Noetherian if it satisfies the descending chain condition for closed subsets: For any sequence of closed subsets
is called Noetherian if it satisfies the descending chain condition for closed subsets: For any sequence of closed subsets 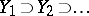 there is an
there is an  such that
such that 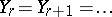 . Now define the (algebraic-geometrically inspired) dimension of
. Now define the (algebraic-geometrically inspired) dimension of 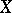 as the supremum of all integers
as the supremum of all integers  such that there exists a chain of irreducible closed subsets
such that there exists a chain of irreducible closed subsets
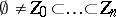 |
(proper inclusions everywhere) in 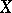 . To avoid confusion, this notion of dimension is written
. To avoid confusion, this notion of dimension is written 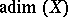 here. This is not a notion which makes a great deal of sense for Hausdorff spaces (the only irreducible Hausdorff spaces are one-point spaces), but it is just right for algebraic varieties and schemes (with the Zariski topology).
here. This is not a notion which makes a great deal of sense for Hausdorff spaces (the only irreducible Hausdorff spaces are one-point spaces), but it is just right for algebraic varieties and schemes (with the Zariski topology).
Indeed, if 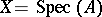 , where
, where 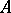 is a commutative Noetherian ring with unit element, then this is the Krull dimension of
is a commutative Noetherian ring with unit element, then this is the Krull dimension of 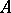 :
: 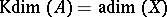 .
.
Let 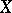 be an irreducible algebraic variety; then
be an irreducible algebraic variety; then 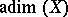 is also the transcendence degree of the field of rational functions on
is also the transcendence degree of the field of rational functions on 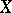 , another frequently used concept to define the dimension of an algebraic variety. The local dimension of
, another frequently used concept to define the dimension of an algebraic variety. The local dimension of 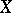 at a point
at a point  is defined as
is defined as 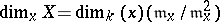 , where
, where 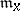 is the maximal ideal of the local ring
is the maximal ideal of the local ring 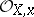 at
at  and
and 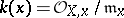 . One has
. One has 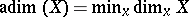 and
and 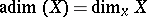 if and only if
if and only if  is a regular point if and only if
is a regular point if and only if 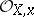 is a regular local ring.
is a regular local ring.
If 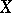 is an algebraic variety over
is an algebraic variety over 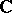 and
and 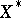 is its open subvariety of smooth points, then
is its open subvariety of smooth points, then 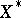 is also a complex manifold over
is also a complex manifold over 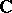 , of
, of 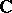 -dimension
-dimension 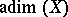 (meaning that locally one needs
(meaning that locally one needs  complex coordinates to describe it) and hence of dimension
complex coordinates to describe it) and hence of dimension 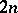 as a topological manifold.
as a topological manifold.
Finally it is possible to describe the topological dimension of a completely-regular space in terms of the algebra 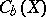 of bounded real-valued functions on
of bounded real-valued functions on 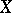 . The metric topology on
. The metric topology on 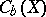 is defined by the norm
is defined by the norm
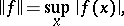 |
which is also determined algebraically by
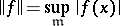 |
where 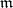 runs through the maximal ideals of
runs through the maximal ideals of 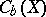 . A subring
. A subring 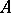 of
of 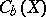 will be called an analytic subring if
will be called an analytic subring if
i) all constant functions belong to 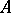 ;
;
ii) 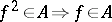 ;
;
iii) 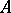 is closed in the metric topology on
is closed in the metric topology on 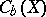 .
.
A set of functions 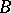 is said to be an analytic base for an analytic subring
is said to be an analytic base for an analytic subring 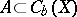 if
if 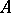 is the smallest analytic subring containing
is the smallest analytic subring containing 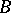 .
.
The following are equivalent for a completely-regular space  : 1)
: 1) 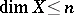 ; 2) every countable set in
; 2) every countable set in  is contained in an analytic subring with analytic base of cardinality
is contained in an analytic subring with analytic base of cardinality 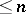 ; and 3) every finite subfamily of
; and 3) every finite subfamily of 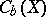 is contained in an analytic subring with an analytic base of cardinality
is contained in an analytic subring with an analytic base of cardinality 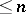 (Katětov's theorem). If
(Katětov's theorem). If 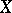 is a compact metric space, these three properties are also equivalent to
is a compact metric space, these three properties are also equivalent to 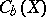 itself having an analytic base of cardinality
itself having an analytic base of cardinality 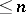 .
.
References
| [a1] | J.M. Gel'fand, A.A. Kirillov, "Sur les corps liés aux algèbres enveloppantes des algèbres de Lie" Publ. Math. IHES , 31 (1966) pp. 5–19 |
| [a2] | R. Gordon, J.C. Robson, "Krull dimension" , Amer. Math. Soc. (1973) |
| [a3] | G. Krause, T.H. Lenagom, "Growth of algebras and Gelfand–Kirillov dimension" , Pitman (1985) |
| [a4] | C. Năstăsecu, F. van Oystaeyen, "Dimensions of ring theory" , Reidel (1987) |
| [a5] | R. Rentschler, P. Gabriel, "Sur la dimension des anneaux et ensembles ordonnées" C.R. Acad. Sci. Paris , 265 (1967) pp. 712–715 |
| [a6] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 272 |
| [a7] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1974) (Translated from Russian) |
| [a8] | L. Gillman, M. Jerison, "Rings of continuous functions" , v. Nostrand (1960) |
| [a9] | N. Bourbaki, "Algèbre commutative" , Masson (1983) pp. Chapt. VIII. Dimension; Chapt. IX. Anneaux locaux noethériens complets |
Dimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dimension&oldid=15750