Diliberto-Straus algorithm
An algorithm first proposed in 1951 by S.P. Diliberto and E.G. Straus [a2]. It is concerned with the problem of finding a best approximation to 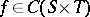 from the subspace
from the subspace 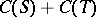 . In the original paper,
. In the original paper, 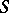 and
and 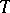 were closed, bounded intervals in
were closed, bounded intervals in 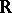 , but there is no difficulty in thinking of them as compact Hausdorff spaces, and then giving
, but there is no difficulty in thinking of them as compact Hausdorff spaces, and then giving 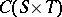 the usual supremum norm (cf. also Approximation theory). The subspace
the usual supremum norm (cf. also Approximation theory). The subspace 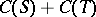 might be more properly written as
might be more properly written as 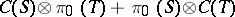 , where
, where 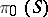 is the subspace of
is the subspace of 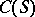 consisting of functions that are constant on
consisting of functions that are constant on 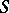 . For
. For 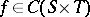 , one defines
, one defines
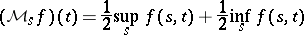 |
and
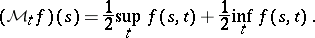 |
The algorithm is then given by 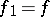 ,
, 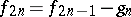 and
and 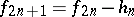 , where
, where 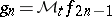 and
and 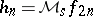 .
.
Diliberto and Straus showed that 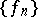 is an equicontinuous family of functions (cf. also Equicontinuity) and that
is an equicontinuous family of functions (cf. also Equicontinuity) and that 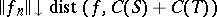 . These two facts may be used to deduce, via the Ascoli theorem, that the sequence
. These two facts may be used to deduce, via the Ascoli theorem, that the sequence 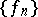 has cluster points (cf. also Cluster set), and that any such cluster point
has cluster points (cf. also Cluster set), and that any such cluster point 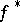 has the property that
has the property that 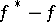 is a closest point to
is a closest point to 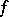 from
from 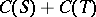 . These results are interesting, because they establish that every
. These results are interesting, because they establish that every 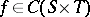 has a best approximation in the infinite-dimensional subspace
has a best approximation in the infinite-dimensional subspace 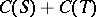 . Diliberto and Straus could not establish that the sequence
. Diliberto and Straus could not establish that the sequence 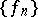 is convergent. However, they came intriguingly near to such a proof when they apparently verified that in the algorithm the incremental functions
is convergent. However, they came intriguingly near to such a proof when they apparently verified that in the algorithm the incremental functions 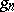 and
and 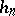 satisfy
satisfy 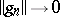 and
and 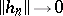 as
as 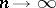 . Unfortunately, a referee demanded that the paper be shortened prior to publication, so the sequence of lemmas needed to establish this result appears without proof. Up till now (1998), no-one has been able to reproduce the series of arguments needed to support some of these lemmas. However, later work by G. Aumann [a1] established that
. Unfortunately, a referee demanded that the paper be shortened prior to publication, so the sequence of lemmas needed to establish this result appears without proof. Up till now (1998), no-one has been able to reproduce the series of arguments needed to support some of these lemmas. However, later work by G. Aumann [a1] established that 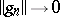 and
and 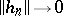 as
as 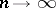 independently of the methods of Diliberto and Straus. Armed with this knowledge, Aumann was able to prove that the Diliberto–Straus algorithm converges. A relatively simple proof of the convergence of the algorithm, which contains Aumann's result on
independently of the methods of Diliberto and Straus. Armed with this knowledge, Aumann was able to prove that the Diliberto–Straus algorithm converges. A relatively simple proof of the convergence of the algorithm, which contains Aumann's result on 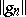 and
and 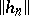 , can be found in [a6].
, can be found in [a6].
Generalizations.
There are two natural generalizations of the Diliberto–Straus algorithm. First, one can continue working in the space 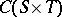 but increase the complexity of the subspace from
but increase the complexity of the subspace from 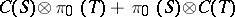 to
to 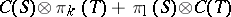 . Here,
. Here, 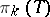 is the subspace of
is the subspace of 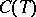 consisting of all polynomials of degree at most
consisting of all polynomials of degree at most 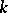 , and
, and 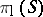 has a similar definition. One has to notice now that the operator
has a similar definition. One has to notice now that the operator 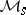 as defined above has the property that, for each
as defined above has the property that, for each 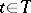 , the number
, the number 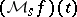 is the best approximation to
is the best approximation to 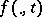 from
from 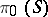 . In the present scenario, the correct generalization is to take the mapping
. In the present scenario, the correct generalization is to take the mapping 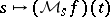 to be the polynomial of degree
to be the polynomial of degree 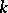 which is the best approximation to
which is the best approximation to 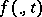 from
from 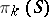 . One can then examine the convergence of the algorithm as before. This was done by N. Dyn [a3], who showed that convergence cannot be guaranteed. In fact, if
. One can then examine the convergence of the algorithm as before. This was done by N. Dyn [a3], who showed that convergence cannot be guaranteed. In fact, if 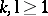 , then there exists a function
, then there exists a function 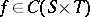 such that the algorithm is stationary, that is,
such that the algorithm is stationary, that is, 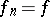 for all
for all 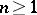 , but
, but 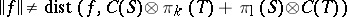 .
.
Another very natural generalization is to consider the algorithm in different spaces. For example, one could examine the behaviour of the analogous algorithm in 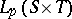 , with the subspace
, with the subspace 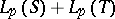 , where
, where 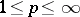 . In the case
. In the case 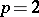 , the algorithm takes place in a Hilbert space, and becomes the alternating algorithm of von Neumann. Because of the uniform convexity of
, the algorithm takes place in a Hilbert space, and becomes the alternating algorithm of von Neumann. Because of the uniform convexity of 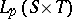 for
for 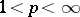 , the analysis of the algorithm can be carried out in considerable generality. The case
, the analysis of the algorithm can be carried out in considerable generality. The case 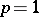 is more delicate. As with the case studied by Dyn, there exist functions
is more delicate. As with the case studied by Dyn, there exist functions 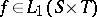 for which the algorithm is stationary, but
for which the algorithm is stationary, but 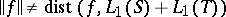 . However, a class of functions
. However, a class of functions 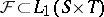 can be identified on which the algorithm can be shown to converge. When working within this set of functions, the task of verifying that the incremental functions satisfy that
can be identified on which the algorithm can be shown to converge. When working within this set of functions, the task of verifying that the incremental functions satisfy that 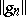 and
and 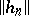 tend to
tend to  is actually easier than the original problem tackled by Aumann. These results can be found in [a4], [a5].
is actually easier than the original problem tackled by Aumann. These results can be found in [a4], [a5].
Finally, it was the intention of Diliberto and Straus to consider approximation of multivariate functions by sums of univariate functions, and their paper gives a number of such results. Other generalizations in 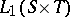 are given in [a7].
are given in [a7].
References
| [a1] | G. Aumann, "Uber approximative nomographie II" Bayer. Akad. Math. Natur. Kl. Sitzungsber. (1959) pp. 103–109 |
| [a2] | S.P. Diliberto, E.G. Straus, "On the approximation of a function of several variables by the sum of functions of fewer variables" Pacific J. Math. , 1 (1951) pp. 195–210 |
| [a3] | N. Dyn, "A straightforward generalization of Diliberto and Straus' algorithm does not work" J. Approx. Th. , 30 : 4 (1980) pp. 247–250 |
| [a4] | W.A. Light, "Convergence of the Diliberto–Straus algorithm in 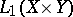 " Numer. Funct. Anal. Optim. , 3 : 2 (1981) pp. 137–146 " Numer. Funct. Anal. Optim. , 3 : 2 (1981) pp. 137–146 |
| [a5] | W.A. Light, "The Diliberto–Straus algorithm in 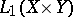 " J. Approx. Th. , 38 : 1 (1983) pp. 1–8 " J. Approx. Th. , 38 : 1 (1983) pp. 1–8 |
| [a6] | W.A. Light, E.W. Cheney, "On the approximation of a bivariate function by the sum of univariate functions" J. Approx. Th. , 29 : 4 (1980) pp. 305–322 |
| [a7] | W.A. Light, S.M. Holland, "The 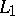 -version of the Diliberto–Straus algorithm in -version of the Diliberto–Straus algorithm in 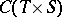 " Proc. Edinburgh Math. Soc. , 27 (1984) pp. 31–45 " Proc. Edinburgh Math. Soc. , 27 (1984) pp. 31–45 |
Diliberto-Straus algorithm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diliberto-Straus_algorithm&oldid=15787