Dihedral group
From Encyclopedia of Mathematics
dihedral group
A group isomorphic to the rotation group of a dihedron, i.e. of a regular doubled pyramid. If the base of the pyramid is an  -gon, the corresponding dihedron group is of order
-gon, the corresponding dihedron group is of order 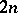 and is generated by two rotations
and is generated by two rotations 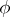 and
and 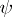 of orders
of orders  and
and  respectively, with the defining relation
respectively, with the defining relation 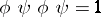 . A dihedral group is sometimes understood to denote the dihedral group of order 8 only. Two different elements of order 2 in any finite group generate a dihedral group.
. A dihedral group is sometimes understood to denote the dihedral group of order 8 only. Two different elements of order 2 in any finite group generate a dihedral group.
References
| [1] | G.G. Hall, "Applied group theory" , Longman (1967) |
How to Cite This Entry:
Dihedral group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dihedral_group&oldid=14889
Dihedral group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dihedral_group&oldid=14889
This article was adapted from an original article by V.D. Mazurov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article