Differential inequality
An inequality which interconnects the argument, the unknown function and its derivatives, e.g.
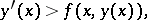 | (1) |
where  is an unknown function of the argument
is an unknown function of the argument  . The principal problem in the theory of differential inequalities is to describe, starting from a known differential inequality and additional (initial or boundary) conditions, all its solutions.
. The principal problem in the theory of differential inequalities is to describe, starting from a known differential inequality and additional (initial or boundary) conditions, all its solutions.
Differential inequalities obtained from differential equations by replacing the equality sign by the inequality sign — which is equivalent to adding some non-specified function of definite sign to one of the sides of the equation — form a large class. A comparison of the solutions of such inequalities with the solutions of the corresponding differential equations is of interest. Thus, the following estimates [1] are valid for any solution of (1):
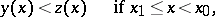 | (2) |
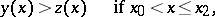 |
where
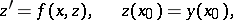 |
on any interval  of existence of both solutions. This simple statement is extensively employed in estimating the solutions of differential equations (by passing to the respective differential inequality with a particular solution which is readily found), the domain of extendability of solutions, the difference between two solutions, in deriving conditions for the uniqueness of a solution, etc. A similar theorem [2] is also valid for a differential inequality (Chaplygin's inequality) of the type
of existence of both solutions. This simple statement is extensively employed in estimating the solutions of differential equations (by passing to the respective differential inequality with a particular solution which is readily found), the domain of extendability of solutions, the difference between two solutions, in deriving conditions for the uniqueness of a solution, etc. A similar theorem [2] is also valid for a differential inequality (Chaplygin's inequality) of the type
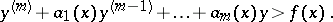 |
Here, estimates of the type (2) for solutions satisfying identical initial conditions at 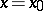 are only certainly true on some interval determined by the coefficients
are only certainly true on some interval determined by the coefficients  . E.g., this is the interval
. E.g., this is the interval 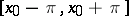 for
for 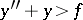 .
.
For a system of differential inequalities
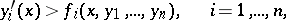 |
it has been shown [3] that if each function 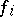 is non-decreasing with respect to the arguments
is non-decreasing with respect to the arguments 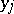 (for all
(for all  ), the estimate
), the estimate
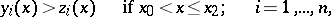 |
resembling (2), is valid. The development of these considerations leads to the theory of differential inequalities in spaces with a cone.
A variant of differential inequalities is the requirement that the total derivative of a given function is of constant sign:
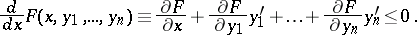 |
This requirement is used in stability theory.
A representative of another class is the differential inequality
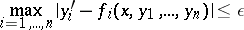 | (3) |
(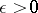 is given), which was first studied in the context of the general idea of an approximate description of a real problem by differential equations [4]. Here the description of the integral funnel, i.e. the set of all points of all solutions which satisfy the given initial conditions, in particular, the behaviour of the funnel as
is given), which was first studied in the context of the general idea of an approximate description of a real problem by differential equations [4]. Here the description of the integral funnel, i.e. the set of all points of all solutions which satisfy the given initial conditions, in particular, the behaviour of the funnel as  , is of interest. A natural generalization of the differential inequality (3) is a differential equation in contingencies, specified by a field of cones, which generalizes the concept of a field of directions.
, is of interest. A natural generalization of the differential inequality (3) is a differential equation in contingencies, specified by a field of cones, which generalizes the concept of a field of directions.
The theory of boundary value problems was also studied for differential inequalities. The inequality  , where
, where  is the Laplace operator, defines subharmonic functions; the differential inequality
is the Laplace operator, defines subharmonic functions; the differential inequality 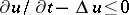 defines subparabolic functions. Studies were also made of differential inequalities of a more general type (in both the above classes) with partial derivatives for differential operators of various types.
defines subparabolic functions. Studies were also made of differential inequalities of a more general type (in both the above classes) with partial derivatives for differential operators of various types.
References
| [1] | M. Petrovitsch, "Sur une manière d'étendre le théorème de la moyence aux équations différentielles du premier ordre" Math. Ann. , 54 : 3 (1901) pp. 417–436 |
| [2] | S.A. Chaplygin, "Fundamentals of a new method of approximate integration of differential equations" , Moscow (1919) (In Russian) |
| [3] | T. Wazewski, "Systèmes des équations et des inégualités différentielles ordinaires aux deuxièmes membres monotones et leurs applications" Ann. Soc. Polon. Math. , 23 (1950) pp. 112–166 |
| [4] | P. Bohl, "Ueber Differentialungleichungen" J. Reine Angew. Math. , 144 (1914) pp. 284–313 |
| [5] | A. Haar, "Ueber Eindeutigkeit und analyzität der Lösungen partieller Differentialgleichungen" , Atti congress. internaz. mathematici (Bologna, 1928) , 3 , Zanichelli (1930) pp. 5–10 |
| [6] | W. Walter, "Differential- und Intergralgleichungen und ihre Anwendung bei Abschätzungs- und Eindeutigkeitsproblemen" , Springer (1964) |
| [7] | J. Szarski, "Differential inequalities" , PWN (1965) |
| [8] | V. Lakshmikantham, S. Leela, "Differential and integral inequalities" , 1–2 , Acad. Press (1969) |
Comments
More generally one considers functional inequalities and integral inequalities of the form
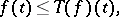 |
where  is a mapping of some space
is a mapping of some space  of functions on an interval into itself. Two useful uniqueness theorems in this setting are as follows. Let
of functions on an interval into itself. Two useful uniqueness theorems in this setting are as follows. Let 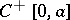 be the space of non-negative continuous functions on
be the space of non-negative continuous functions on  . Let
. Let 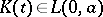 be continuous and non-negative. Now, if for
be continuous and non-negative. Now, if for  ,
,
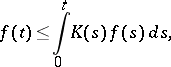 |
then  is identically zero. Now let
is identically zero. Now let 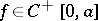 be such that
be such that  and
and 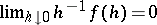 . Then if
. Then if
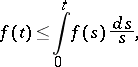 |
also 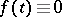 (Nagumo's lemma). let
(Nagumo's lemma). let  , let
, let  and suppose
and suppose
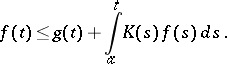 |
Then
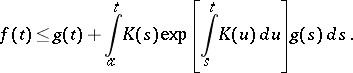 |
The last result is known as Gronwall's lemma (Gronwall's inequality). The case  is important. Another variant of Gronwall's lemma is as follows. Let
is important. Another variant of Gronwall's lemma is as follows. Let  and for some constant
and for some constant  ,
,
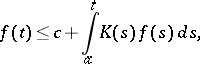 |
then
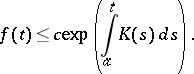 |
This last result is useful in discussing, e.g., the stability of (constantly acting) perturbations 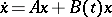 (with
(with 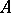 constant) in terms of the stability of
constant) in terms of the stability of 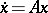 .
.
References
| [a1] | D.W. Jordan, P. Smith, "Nonlinear ordinary differential equations" , Clarendon Press (1977) |
| [a2] | E. Hille, "Ordinary differential equations in the complex plane" , Wiley (Interscience) (1976) |
Differential inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_inequality&oldid=30823