Differential inclusion
multi-valued differential equation, differential equation with multi-valued right-hand side
A relation
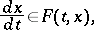 | (1) |
where  is an unknown vector function on some interval and
is an unknown vector function on some interval and  is a set in an
is a set in an  -dimensional space which depends on the number
-dimensional space which depends on the number  and on the vector
and on the vector  . The solution of a differential inclusion (1) is usually understood to mean an absolutely-continuous vector function
. The solution of a differential inclusion (1) is usually understood to mean an absolutely-continuous vector function  which satisfies the relation
which satisfies the relation
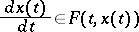 |
almost-everywhere on the interval of variation of  under consideration. In particular, if the set
under consideration. In particular, if the set 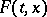 consists of a single point, a differential inclusion becomes an ordinary differential equation
consists of a single point, a differential inclusion becomes an ordinary differential equation 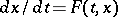 . Equations of the type
. Equations of the type 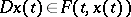 where
where 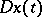 is a contingent, [1], are equivalent to differential inclusions in a large number of cases.
is a contingent, [1], are equivalent to differential inclusions in a large number of cases.
Differential inclusions are generated, for example, by the problem concerning functions which satisfy a differential equation to within required accuracy
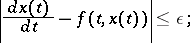 |
by differential inequalities
 |
by differential equations with discontinuous right-hand side [1], Chapt. 2; and by problems in the theory of optimal control [3], [2]. The equation which is most often considered in control problems is
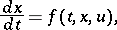 | (2) |
where 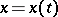 is the vector function sought, while
is the vector function sought, while 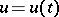 is the control, i.e. a vector function which may be arbitrarily chosen out of all permissible controls (i.e. such that
is the control, i.e. a vector function which may be arbitrarily chosen out of all permissible controls (i.e. such that 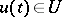 for each
for each 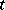 , where
, where 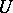 is a given set which may depend on
is a given set which may depend on  and on
and on 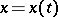 ). The set of solutions of equation (2) for all permissible controls
). The set of solutions of equation (2) for all permissible controls 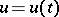 satisfies the differential inclusion (1), where
satisfies the differential inclusion (1), where 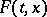 is the set of all values of the function
is the set of all values of the function 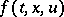 when
when  runs through the set
runs through the set 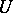 .
.
In the theory of differential inclusions it is usually assumed that for any 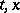 from the domain
from the domain 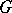 under consideration the set
under consideration the set 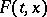 is a non-empty closed bounded set in an
is a non-empty closed bounded set in an  -dimensional space. If the set
-dimensional space. If the set  is everywhere convex, and, for any
is everywhere convex, and, for any  , it is an upper semi-continuous function in
, it is an upper semi-continuous function in  (i.e. for any
(i.e. for any 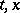 and any
and any  the set
the set 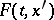 is contained in the
is contained in the  -neighbourhood of the set
-neighbourhood of the set 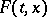 for all sufficiently small
for all sufficiently small 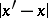 ), while for any
), while for any  it is a measurable function of
it is a measurable function of 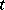 (i.e. for any
(i.e. for any  and any sphere
and any sphere 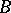 in the
in the  -dimensional space, the set of values of
-dimensional space, the set of values of 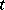 for which the set
for which the set  is non-empty is Lebesgue measurable), and if also
is non-empty is Lebesgue measurable), and if also 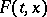 is always contained in a sphere
is always contained in a sphere  where the function
where the function 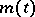 is Lebesgue integrable, then, for any initial conditions
is Lebesgue integrable, then, for any initial conditions 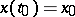 ,
, 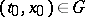 , a solution of the differential inclusion exists [4] and the integral funnel consisting of such solutions displays the usual properties [4]. The requirement that the set
, a solution of the differential inclusion exists [4] and the integral funnel consisting of such solutions displays the usual properties [4]. The requirement that the set  be convex may be dropped if it depends continuously on
be convex may be dropped if it depends continuously on  . The existence of a solution is preserved [5], but the properties of the integral funnels are not.
. The existence of a solution is preserved [5], but the properties of the integral funnels are not.
For a review of the publications on differential inclusions and on the connection of such inclusions with control problems see [6], [7]. For the concept of stability of differential inclusions see [8], [1]; for the existence of bounded and periodic solutions, and for other properties, see [1], [6], [7].
References
| [1] | A.F. Filippov, "Differential equations with discontinuous righthand sides" , Reidel (1988) (Translated from Russian) |
| [2] | A. Wazewski, "Systèmes de commande et équations au contingent" Bull. Acad. Polon. Sci. Ser. Math. , 9 : 3 (1961) pp. 151–155 |
| [3] | A.F. Filoppov, "On certain questions in the theory of optimal control" SIAM J. Control Ser. A , 1 : 1 (1962) pp. 76–84 Vestnik Moskov. Univ. Ser. Mat. Mekh. Astr. , 2 (1959) pp. 25–32 |
| [4] | J.L. Davy, "Properties of the solution set of a generalized differential equation" Bull. Austr. Math. Soc. , 6 : 3 (1972) pp. 379–398 |
| [5] | C. Olech, "Existence of solutions of non-convex orientor fields" Boll. Un. Mat. Ital. , 11 : 3 (1975) pp. 189–197 |
| [6] | V.I. Blagodatskikh, A.F. Filippov, "Differential inclusions and optimal control" Proc. Steklov Inst. Math. , 169 (To appear) Trudy Mat. Inst. Steklov. , 169 (To appear) |
| [7] | J.-P. Aubin, A. Cellina, "Differential inclusions" , Univ. Paris IX (1983) |
| [8] | E. Roxin, "Stability in general control systems" J. Diff. Equations , 1 : 2 (1965) pp. 115–150 |
Differential inclusion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_inclusion&oldid=13723