Differential form
A differential form of degree  , a
, a 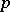 -form, on a differentiable manifold
-form, on a differentiable manifold 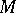 is a
is a 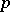 times covariant tensor field on
times covariant tensor field on 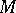 . It may also be interpreted as a
. It may also be interpreted as a 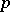 -linear (over the algebra
-linear (over the algebra 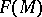 of smooth real-valued functions on
of smooth real-valued functions on 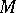 ) mapping
) mapping 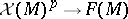 , where
, where 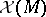 is the
is the 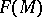 -module of smooth vector fields on
-module of smooth vector fields on 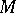 . Forms of degree one are also known as Pfaffian forms. An example of such a form is the differential
. Forms of degree one are also known as Pfaffian forms. An example of such a form is the differential 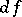 of a smooth function
of a smooth function 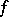 on
on 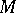 , which is defined as follows:
, which is defined as follows: 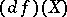 ,
, 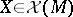 , is the derivative
, is the derivative 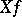 of
of 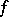 in the direction of the field
in the direction of the field 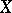 . Riemannian metrics on a manifold
. Riemannian metrics on a manifold 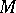 serve as examples of symmetric differential forms of degree two. However, the term "differential form" is often used to denote skew-symmetric or exterior differential forms, which have the greatest number of applications.
serve as examples of symmetric differential forms of degree two. However, the term "differential form" is often used to denote skew-symmetric or exterior differential forms, which have the greatest number of applications.
If 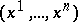 is a local system of coordinates in a domain
is a local system of coordinates in a domain 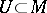 , the forms
, the forms 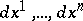 constitute a basis of the cotangent space
constitute a basis of the cotangent space 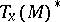 ,
, 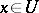 . For this reason (cf. Exterior algebra) any exterior
. For this reason (cf. Exterior algebra) any exterior  -form
-form 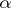 may be written in
may be written in 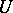 in the form
in the form
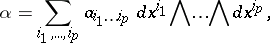 | (1) |
where the 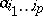 are functions on
are functions on 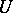 . In particular,
. In particular,
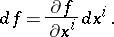 |
Let 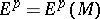 be the space of all exterior
be the space of all exterior 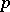 -forms of class
-forms of class 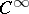 , where
, where 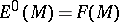 . The exterior multiplication
. The exterior multiplication 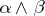 converts
converts 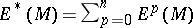 (where
(where  ) to an associative graded algebra over
) to an associative graded algebra over 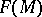 which satisfies the condition of graded commutativity
which satisfies the condition of graded commutativity
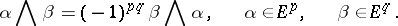 | (2) |
A smooth mapping between manifolds 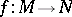 induces a homomorphism
induces a homomorphism 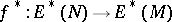 between
between 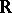 -algebras.
-algebras.
The concept of the differential of a function is generalized as follows. For any 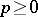 there exists a unique
there exists a unique 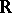 -linear mapping
-linear mapping 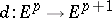 (exterior differentiation), which for
(exterior differentiation), which for 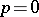 coincides with the differential introduced above, with the following properties:
coincides with the differential introduced above, with the following properties:
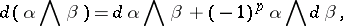 |
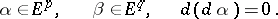 |
The exterior differential of a form 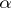 written in in local coordinates (see (1)) is expressed by the formula
written in in local coordinates (see (1)) is expressed by the formula
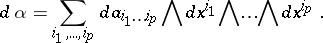 |
Its coordinate-free notation is
 |
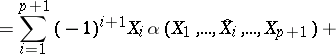 |
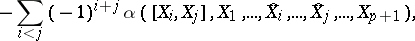 |
where 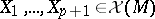 . The Lie derivative operator
. The Lie derivative operator 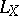 ,
, 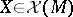 , on differential forms is connected with the exterior differentiation operator by the relation
, on differential forms is connected with the exterior differentiation operator by the relation
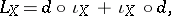 |
where 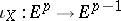 is the operator of interior multiplication by
is the operator of interior multiplication by 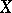 :
:
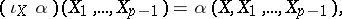 |
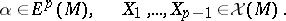 |
The complex 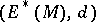 is a cochain complex (the de Rham complex). The cocycles of this complex are said to be closed forms, while the coboundaries are known as exact forms. According to the de Rham theorem, the cohomology algebra
is a cochain complex (the de Rham complex). The cocycles of this complex are said to be closed forms, while the coboundaries are known as exact forms. According to the de Rham theorem, the cohomology algebra
 |
of the de Rham complex is isomorphic to the real cohomology algebra 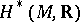 of the manifold
of the manifold 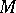 . In particular,
. In particular, 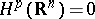 if
if 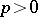 (Poincaré's lemma).
(Poincaré's lemma).
The de Rham theorem is closely connected with another operation, that of integration of differential forms. Let 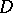 be a bounded domain in
be a bounded domain in 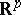 and let
and let  be a smooth mapping
be a smooth mapping 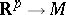 , defined in a neighbourhood of the closure
, defined in a neighbourhood of the closure 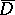 . If
. If 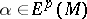 , then
, then 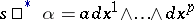 , where
, where  is a smooth function in
is a smooth function in  . The integral of the form
. The integral of the form 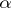 over the surface
over the surface  is defined by the formula:
is defined by the formula:
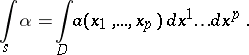 |
If the boundary of 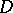 is piecewise smooth, the formula
is piecewise smooth, the formula
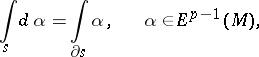 | (3) |
is valid; here 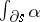 is defined as the sum of the integrals of the form
is defined as the sum of the integrals of the form  over the smooth pieces of the boundary, provided with their natural parametrizations. The classical formulas of Newton–Leibniz, Green–Ostrogradski and Stokes (see also Stokes theorem) are all special cases of this formula. By virtue of formula (3) each closed
over the smooth pieces of the boundary, provided with their natural parametrizations. The classical formulas of Newton–Leibniz, Green–Ostrogradski and Stokes (see also Stokes theorem) are all special cases of this formula. By virtue of formula (3) each closed 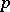 -form
-form  defines a
defines a 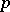 -dimensional singular cocycle whose value on the simplex
-dimensional singular cocycle whose value on the simplex  is
is 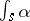 . This correspondence is a realization of the isomorphism given by de Rham's theorem.
. This correspondence is a realization of the isomorphism given by de Rham's theorem.
Formula (3) was published in 1899 by H. Poincaré [2], who regarded exterior forms as integrand expressions in integral invariants. At the same time E. Cartan [3] gave an almost-modern definition of exterior forms and of the exterior differentiation operator (at first on Pfaffian forms), stressing the connection between his own construction and exterior algebra.
As well as the exterior scalar forms defined above, one may also study exterior differential forms with values in a vector space 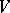 over
over 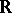 . If
. If 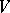 is an algebra, then a natural multiplication (an extension of the exterior multiplication) is defined on the space
is an algebra, then a natural multiplication (an extension of the exterior multiplication) is defined on the space 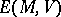 of forms with values in
of forms with values in 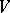 . If the algebra
. If the algebra 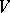 is also associative,
is also associative, 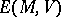 is associative as well; if
is associative as well; if 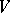 is commutative,
is commutative, 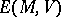 is graded-commutative (formula (2)); if
is graded-commutative (formula (2)); if 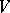 is a Lie algebra, then
is a Lie algebra, then  is a graded Lie algebra. The following, even more general, concept is also often considered. Let
is a graded Lie algebra. The following, even more general, concept is also often considered. Let 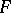 be a smooth vector bundle with base
be a smooth vector bundle with base 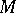 . If for each point
. If for each point 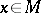 there is given a skew-symmetric
there is given a skew-symmetric 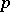 -linear function on
-linear function on 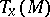 with values in the fibre
with values in the fibre 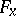 of the bundle
of the bundle 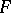 , a so-called
, a so-called 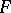 -valued
-valued 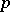 -form is obtained. An
-form is obtained. An 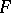 -valued
-valued 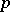 -form can also be interpreted as a
-form can also be interpreted as a 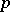 -linear (over
-linear (over  ) mapping of the module
) mapping of the module 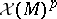 into the module of smooth sections of
into the module of smooth sections of 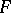 . The space of such forms is denoted by
. The space of such forms is denoted by 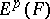 . If
. If 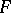 is given by locally constant transition functions or, which amounts to the same thing, if a flat connection is specified on
is given by locally constant transition functions or, which amounts to the same thing, if a flat connection is specified on 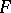 , it is possible to define the de Rham complex and to generalize the de Rham theorem to this case.
, it is possible to define the de Rham complex and to generalize the de Rham theorem to this case.
Forms with values in the tangent bundle 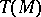 are also called vector differential forms; these forms may be identified with
are also called vector differential forms; these forms may be identified with 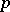 times covariant and one time contravariant tensor fields on
times covariant and one time contravariant tensor fields on 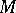 which are skew-symmetric with respect to the covariant indices. Vector differential forms are used to describe the derivations of the algebra of exterior forms
which are skew-symmetric with respect to the covariant indices. Vector differential forms are used to describe the derivations of the algebra of exterior forms 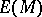 [4]. Vector forms (as well as their generalization — jet forms) are used in the theory of deformations of complex and other differential-geometric structures on manifolds.
[4]. Vector forms (as well as their generalization — jet forms) are used in the theory of deformations of complex and other differential-geometric structures on manifolds.
Analogues of differential forms are also constructed in simplicial theory. One such construction, whose idea is due to H. Whitney [5], may be used to calculate the rational cohomology of a simplicial complex 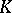 . A piecewise-linear form (or
. A piecewise-linear form (or 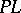 -form) on
-form) on 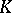 is a compatible family of differential forms defined on the simplices of the complex
is a compatible family of differential forms defined on the simplices of the complex 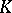 , with polynomials with rational coefficients as coefficients when written in barycentric coordinates. The
, with polynomials with rational coefficients as coefficients when written in barycentric coordinates. The  -forms on
-forms on 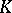 form a graded commutative differential algebra
form a graded commutative differential algebra 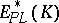 over
over 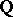 . The integration of forms determines an isomorphism of the cohomology algebra of this algebra onto the algebra
. The integration of forms determines an isomorphism of the cohomology algebra of this algebra onto the algebra 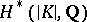 , where
, where 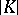 is the polyhedron corresponding to the complex
is the polyhedron corresponding to the complex 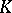 . The algebra
. The algebra  also completely defines the rational homotopy type (in particular, the ranks of homotopy groups) of
also completely defines the rational homotopy type (in particular, the ranks of homotopy groups) of 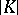 . In a similar manner, the algebra
. In a similar manner, the algebra  on a differentiable manifold
on a differentiable manifold 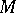 defines the real homotopy type of
defines the real homotopy type of 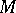 [9], [11].
[9], [11].
The calculus of exterior forms on a complex analytic manifold has a number of special features [6]. In this situation it is usual to consider the space  of complex-valued forms, or the spaces
of complex-valued forms, or the spaces 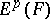 where
where 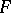 is a holomorphic vector bundle on
is a holomorphic vector bundle on 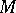 . The following decomposition is valid:
. The following decomposition is valid:
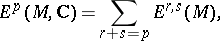 |
where 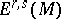 is the space of forms of type
is the space of forms of type 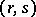 , i.e. of forms
, i.e. of forms 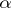 which are locally representable as
which are locally representable as
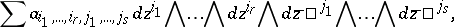 |
where 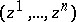 is a local analytic coordinate system on
is a local analytic coordinate system on 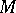 . Similarly,
. Similarly,
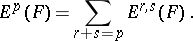 |
Further, 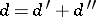 , where
, where
 |
Here 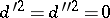 , so that
, so that 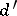 and
and  define cochain complexes. The best known is the complex of the operator
define cochain complexes. The best known is the complex of the operator  (the Dolbeault complex), the cohomology of which is denoted by
(the Dolbeault complex), the cohomology of which is denoted by  .
. 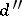 -cocycles of type
-cocycles of type 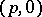 are holomorphic
are holomorphic 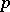 -forms (cf. Holomorphic form). The following Grothendieck lemma is valid for
-forms (cf. Holomorphic form). The following Grothendieck lemma is valid for  : If
: If 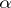 is a form of type
is a form of type  with
with 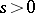 in a neighbourhood of zero of the space
in a neighbourhood of zero of the space 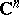 and
and 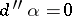 , then a smaller neighbourhood of zero contains a form
, then a smaller neighbourhood of zero contains a form 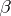 of type
of type  such that
such that 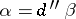 . The Dolbeault complex may also be defined for
. The Dolbeault complex may also be defined for  -valued forms where
-valued forms where 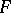 is a holomorphic vector bundle. This leads to the cohomology spaces
is a holomorphic vector bundle. This leads to the cohomology spaces 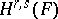 . The Grothendieck lemma implies the following isomorphism:
. The Grothendieck lemma implies the following isomorphism:
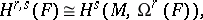 |
where 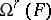 is the sheaf of germs of holomorphic
is the sheaf of germs of holomorphic 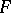 -valued
-valued  -forms (Dolbeault's theorem). In particular,
-forms (Dolbeault's theorem). In particular,
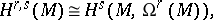 |
where 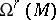 is the sheaf of germs of holomorphic
is the sheaf of germs of holomorphic  -forms on
-forms on 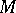 . There exists a spectral sequence with first term
. There exists a spectral sequence with first term 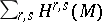 and converging to
and converging to 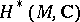 . The Euler characteristic
. The Euler characteristic 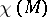 of a compact complex manifold
of a compact complex manifold 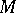 is expressed in terms of the Dolbeault cohomology spaces by the formula
is expressed in terms of the Dolbeault cohomology spaces by the formula
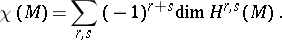 |
Differential forms are an important component of the apparatus of differential geometry [7], . They are also systematically employed in topology, in the theory of differential equations, in mechanics, in the theory of complex manifolds, and in the theory of functions of several complex variables. Currents are a generalization of differential forms, similar to generalized functions. The algebraic analogue of the theory of differential forms (cf. Derivations, module of) makes it possible to define differential forms on algebraic varieties and analytic spaces (cf. Differential calculus (on analytic spaces)). See also de Rham cohomology; Differential on a Riemann surface; Harmonic form; Holomorphic form; Laplace operator.
References
| [1] | G. de Rham, "Differentiable manifolds" , Springer (1984) (Translated from French) |
| [2] | H. Poincaré, "Les méthodes nouvelles de la mécanique céleste" , 3 , Gauthier-Villars (1899) pp. Chapt. 26 |
| [3] | E. Cartan, "Sur certaines expressions différentielles et le problème de Pfaff" , Oeuvres complètes , 1, Pt. 2 , Gauthier-Villars pp. 303–396 |
| [4] | A. Frölicher, A. Nijenhuis, "Theory of vector-valued differential forms. I. Derivations in the graded ring of differential forms" Proc. Koninkl. Ned. Akad. Wet. Ser. A , 59 : 3 (1956) pp. 338–359 |
| [5] | H. Whitney, "Geometric integration theory" , Princeton Univ. Press (1957) |
| [6] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
| [7] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
| [8a] | H. Cartan, "Calcul différentiel" , Hermann (1967) |
| [8b] | H. Cartan, "Formes différentielles" , Hermann (1967) |
| [9] | P. Deligne, P. Griffiths, J. Morgan, D. Sullivan, "The real homotopy of Kaehler manifolds" Invent. Math. , 29 (1975) pp. 245–274 |
| [10] | R. Bott, L.W. Tu, "Differential forms in algebraic topology" , Springer (1982) |
| [11] | D. Sullivan, "Infinitesimal computations in topology" Publ. Math. IHES , 47 (1977) pp. 269–331 |
Comments
In the Western literature, by a differential 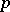 -form on a differentiable manifold
-form on a differentiable manifold 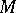 one always means a smooth section of the
one always means a smooth section of the 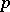 -th exterior power of the tangent bundle
-th exterior power of the tangent bundle 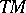 , i.e. a smooth section of
, i.e. a smooth section of 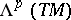 . (These are called exterior differential forms in the main article.)
. (These are called exterior differential forms in the main article.)
The value of the operator 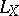 on a differential form
on a differential form  is also called the pullback of
is also called the pullback of  under the infinitesimal transformation generated by the vector field
under the infinitesimal transformation generated by the vector field 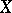 .
.
Let 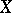 be a
be a  -manifold of dimension
-manifold of dimension  . A current on
. A current on 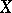 is a linear functional defined on the space
is a linear functional defined on the space 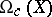 of smooth (anti-symmetric) differential forms of compact support on
of smooth (anti-symmetric) differential forms of compact support on 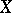 . The current
. The current 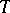 is said to be homogeneous of dimension
is said to be homogeneous of dimension 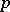 if
if 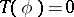 for all
for all 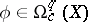 with
with 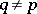 .
.
The degree of a current 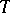 is
is  , if
, if 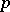 is its dimension (if
is its dimension (if 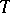 is homogeneous).
is homogeneous).
Define a chain element in 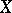 (of dimension
(of dimension 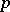 ) as a smooth mapping
) as a smooth mapping 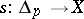 of the standard cube of dimension
of the standard cube of dimension 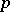 into
into 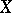 . If
. If 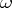 is a
is a 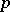 -form on
-form on 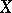 , then
, then 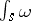 is defined as
is defined as 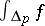 if
if 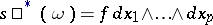 (cf. the main article above). If
(cf. the main article above). If  is smooth and orientation-preserving, the integral
is smooth and orientation-preserving, the integral 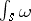 only depends on the image
only depends on the image 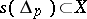 (and on
(and on 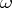 over
over 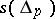 ). More generally, a
). More generally, a 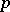 -chain on a manifold
-chain on a manifold 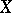 is a formal linear combination
is a formal linear combination 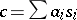 of chain elements. The corresponding integral is defined as
of chain elements. The corresponding integral is defined as 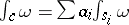 . Each
. Each 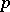 -chain thus defines a current on
-chain thus defines a current on 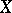 of dimension
of dimension 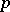 and degree
and degree 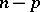 . If
. If 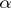 is a
is a 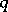 -form, it defines a homogeneous
-form, it defines a homogeneous  current by the formula
current by the formula 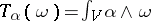 . Let
. Let 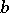 be a contravariant
be a contravariant 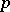 -vector with local coordinates
-vector with local coordinates 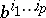 . Let the local coordinates of the
. Let the local coordinates of the 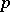 -form
-form 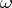 be
be 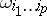 ; then
; then
 |
defines a current of dimension 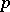 . Thus, currents generalize both forms (i.e. covariant vectors) and contravariant vectors. They are also a global generalization of the idea of distributions (as a generalization of functions). The role of a space of test functions is played by the smooth forms of compact support. The name "current" comes from the fact that in
. Thus, currents generalize both forms (i.e. covariant vectors) and contravariant vectors. They are also a global generalization of the idea of distributions (as a generalization of functions). The role of a space of test functions is played by the smooth forms of compact support. The name "current" comes from the fact that in 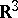 the currents of dimension 1 can be interpreted as electric currents.
the currents of dimension 1 can be interpreted as electric currents.
In the theory of several complex variables one defines the currents of type 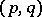 over a domain
over a domain 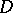 as the (complex-valued) linear functionals on the space
as the (complex-valued) linear functionals on the space  of
of  (complex-valued) forms with compact support. In this area currents and their applications are a very active field of research at the moment [a2].
(complex-valued) forms with compact support. In this area currents and their applications are a very active field of research at the moment [a2].
References
| [a1] | E.M. Chirka, "Complex analytic sets" , Kluwer (1989) (Translated from Russian) |
| [a2] | P. Lelong, L. Gruman, "Entire functions of several complex variables" , Springer (1986) |
A differential form on an algebraic variety is the analogue of the concept of a differential form on a differentiable manifold. Let 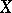 be an irreducible algebraic variety of dimension
be an irreducible algebraic variety of dimension 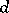 over an algebraically closed field
over an algebraically closed field 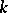 (cf. Irreducible variety) and let
(cf. Irreducible variety) and let 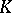 be its field of rational functions. A differential form of degree
be its field of rational functions. A differential form of degree  on
on 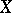 is an element of the
is an element of the 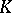 -space
-space
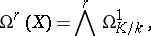 |
where 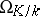 is the module of derivations (cf. Derivations, module of) of the field
is the module of derivations (cf. Derivations, module of) of the field 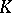 over the field
over the field 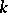 . If
. If  is a separable basis of transcendency of the extension
is a separable basis of transcendency of the extension 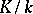 , any differential form
, any differential form 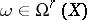 can be written as
can be written as
 |
where 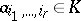 . A differential form
. A differential form 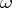 is called regular on an open set
is called regular on an open set 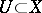 if
if 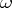 belongs to the submodule
belongs to the submodule 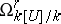 of
of 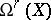 , regarded as a module over the ring
, regarded as a module over the ring 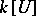 of regular functions on the subset
of regular functions on the subset 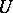 . A differential form
. A differential form 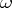 is called regular if any point
is called regular if any point 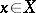 has a neighbourhood
has a neighbourhood 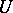 such that
such that 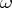 is regular on
is regular on 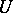 . The regular differential forms on
. The regular differential forms on 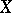 form a module over
form a module over 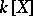 , denoted by
, denoted by 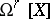 . Its elements are identified with the sections of the sheaf
. Its elements are identified with the sections of the sheaf 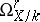 over the variety
over the variety 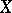 . In a neighbourhood of each point
. In a neighbourhood of each point 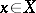 a regular differential form
a regular differential form  is written as
is written as
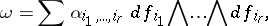 |
where the functions 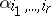 ,
,  are regular at the point
are regular at the point  . If
. If 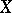 is a complete algebraic variety, the spaces
is a complete algebraic variety, the spaces 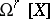 are finite-dimensional, and if
are finite-dimensional, and if 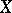 is non-singular, the dimension
is non-singular, the dimension 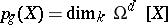 is known as the geometric genus of the variety
is known as the geometric genus of the variety 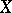 . If
. If 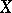 is a complete variety over the field of complex numbers, the space
is a complete variety over the field of complex numbers, the space 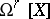 is identical with the space of holomorphic differential forms of degree
is identical with the space of holomorphic differential forms of degree  on the corresponding analytic space
on the corresponding analytic space  .
.
Let 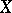 be a normal variety and let
be a normal variety and let 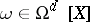 ; for any point
; for any point 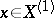 of codimension one the differential form
of codimension one the differential form 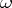 may be written as
may be written as
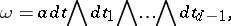 | (*) |
where  belongs to the field of fractions
belongs to the field of fractions  of the local ring
of the local ring 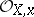 ,
, 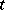 is the generator of its maximal ideal, and
is the generator of its maximal ideal, and 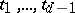 is a separable basis of transcendency over
is a separable basis of transcendency over 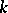 of the residue field of the ring
of the residue field of the ring 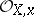 . The value of the valuation at the element
. The value of the valuation at the element  , as defined by the ring
, as defined by the ring 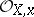 , does not depend on the choice of the representation of
, does not depend on the choice of the representation of 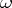 in the form (*) and is denoted by
in the form (*) and is denoted by 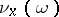 . The divisor
. The divisor
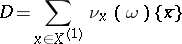 |
is defined and is known as divisor of the differential form 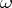 . A differential form
. A differential form 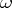 is regular if and only if its divisor
is regular if and only if its divisor 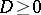 , i.e.
, i.e. 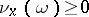 for all
for all 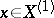 . The divisors of any two differential forms are equivalent and, moreover, the divisors of all differential forms on a given algebraic variety form a divisor class with respect to linear equivalence. This class is known as the canonical class of the variety
. The divisors of any two differential forms are equivalent and, moreover, the divisors of all differential forms on a given algebraic variety form a divisor class with respect to linear equivalence. This class is known as the canonical class of the variety 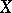 and is denoted by
and is denoted by 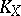 . For a non-singular variety
. For a non-singular variety 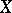 the class
the class 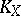 is identical with the first Chern class of the invertible sheaf
is identical with the first Chern class of the invertible sheaf 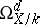 ; in particular,
; in particular,
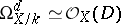 |
for any 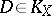 .
.
Any dominant rational mapping between algebraic varieties 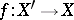 induces a canonical homomorphism
induces a canonical homomorphism
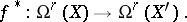 |
If 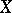 and
and 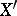 are non-singular and
are non-singular and 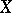 is complete,
is complete, 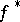 maps regular differential forms to regular ones. In particular, if two non-singular complete varieties
maps regular differential forms to regular ones. In particular, if two non-singular complete varieties 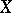 and
and 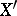 are birationally isomorphic, the vector spaces
are birationally isomorphic, the vector spaces 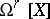 and
and 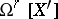 are isomorphic over the field
are isomorphic over the field 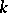 .
.
For any 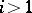 the elements of the
the elements of the 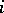 -th symmetric power
-th symmetric power 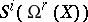 of the
of the 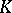 -space
-space 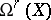 are known as
are known as  -tuple differential forms of degree
-tuple differential forms of degree  on
on 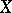 . Each such differential form may be considered as a rational section of the sheaf
. Each such differential form may be considered as a rational section of the sheaf 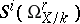 . The regular sections
. The regular sections
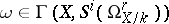 |
are known as regular 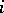 -tuple differential forms of degree
-tuple differential forms of degree  on
on 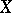 . For a non-singular complete variety
. For a non-singular complete variety 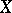 the dimension
the dimension
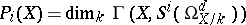 |
is known as the 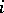 genus of the variety
genus of the variety 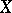 . The
. The 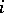 genera of birationally isomorphic varieties are identical.
genera of birationally isomorphic varieties are identical.
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
| [2] | M. Baldassarri, "Algebraic varieties" , Springer (1956) |
| [3] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
I.V. Dolgachev
Comments
In terms of the description of (Cartier) divisors by local functions (cf. Divisor), the divisor associated to a differential form 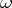 of degree
of degree  ,
, 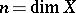 ,
,  smooth, can be described as follows. For each
smooth, can be described as follows. For each 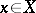 there is an open affine
there is an open affine 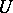 such that
such that 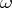 can be represented in
can be represented in 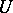 as
as 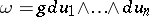 . Now cover
. Now cover 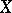 by open affine
by open affine 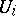 . Let the representation of
. Let the representation of 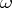 in
in 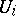 be
be 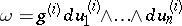 . Then on
. Then on  ,
, 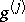 is equal to
is equal to 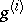 times the Jacobian of the
times the Jacobian of the 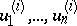 with respect to the
with respect to the 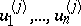 . Thus the local functions
. Thus the local functions 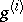 on
on 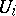 define a divisor on
define a divisor on 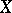 , denoted by
, denoted by 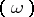 . One has
. One has 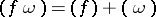 for all
for all 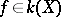 and thus, because
and thus, because 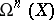 is one-dimensional over
is one-dimensional over 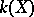 , all
, all 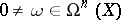 define the same divisor class, the canonical class (canonical divisor class) of
define the same divisor class, the canonical class (canonical divisor class) of  .
.
Differential form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_form&oldid=19108