Differential equations on a torus
flows on a torus
A class of dynamical systems (cf. Dynamical system). An example is the flow generated by all translations of a torus (considered as a Lie group) by the elements of some one-parameter subgroup of the torus. In "angular" or "cyclic" coordinates on the torus counted modulo 1 (which may be considered as ordinary coordinates in a Euclidean space $ \mathbf R ^ {n} $ from which the torus $ T ^ {n} $ is obtained as a quotient group modulo the integer lattice $ \mathbf Z ^ {n} $), this flow is described as follows: Within time $ t $ a point $ x = ( x _ {1} \dots x _ {n} ) $ transforms to the point
$$ \tag{1 } T ^ {t} x = x + t \omega , $$
where $ \omega = ( \omega _ {1} \dots \omega _ {n} ) $ is the set of so-called basic frequencies. All trajectories of this flow are quasi-periodic functions (cf. Quasi-periodic function) of time; their properties are determined by the arithmetical properties of the basic frequencies. Thus, the trajectories are periodic if all $ \omega _ {i} $ are integer multiples of the same number. In the other extreme case, when the $ \omega _ {i} $ are linearly independent over $ \mathbf Z $( i.e. no non-trivial linear combination $ \sum k _ {i} \omega _ {i} $ with integers $ k _ {i} $ is equal to zero), each trajectory is dense in the torus (an irrational winding of the torus), while the flow is ergodic (with respect to Haar measure on $ T ^ {n} $; Haar measure is naturally obtained from Lebesgue measure in $ \mathbf R ^ {n} $ under factorization by $ \mathbf Z ^ {n} $ and is preserved under the translations $ T ^ {t} $) and is even strictly ergodic; its spectrum is discrete.
Such flows often appear in various problems. Thus, in the case of integrable Hamiltonian systems (cf. Hamiltonian system), "typical" motions with compact support (i.e. remaining in a finite domain of the phase space) lead to such flows (the corresponding tori are level manifolds of the system of first integrals [8]). Such invariant tori with irrational windings are also frequently encountered in Hamiltonian systems sufficiently close to integrable ones (this problem is closely connected with small denominators).
The possible types of qualitative behaviour of trajectories of flows without equilibrium positions were fully clarified for a two-dimensional torus by H. Poincaré [1], A. Denjoy [2] (see also [3]) and H. Kneser [4] (for a modified presentation see [5], [6]). (Of all closed surfaces, only the torus and the Klein surface admit such flows, while the study of flows on the latter surface can be reduced, in principle, to the study of flows on the torus which is its two-sheeted covering surface.)

Figure: d032070a
The following is known about these flows. If there is a doubly-connected domain (a "Kneser ringKneser ring" ) on the surface, bounded by two closed trajectories, while inside that domain the trajectories spiral away from one of them and spiral towards the other in the opposite direction (see Fig.), then the qualitative behaviour of the trajectories on the surface resembles that of the trajectories in a bounded domain in the plane. In particular, all non-periodic trajectories in both time directions tend to become periodic. The case (which is possible only on a torus) when there are no Kneser rings is more interesting; this is equivalent to the existence of a closed transversal $ L $( i.e. a closed curve which is nowhere tangent to the trajectories) intersecting each trajectory an infinite number of times. On $ L $ the Poincaré return map of $ S $ — the homeomorphism sending a point $ x \in L $ into the first intersection point of the positive semi-trajectory through $ x $ with $ L $ — is defined. The cascade $ \{ S ^ {n} \} $ on $ L $ is characterized by its Poincaré rotation number $ \alpha $( see, for example, [3]; it is partly dependent on the specific choice of $ L $; the asymptotic cycle is a completely-invariant characteristic of the original flow [14]). According to Denjoy's theorem, if $ S $ is of class $ C ^ {2} $( which is always the case if the transversal and the initial flow on the torus are both suitably smooth), while $ \alpha $ is irrational, then $ S $ is topologically conjugate to the rotation of the circle through the angle $ 2 \pi \alpha $, i.e. it is possible to introduce a cyclic coordinate $ x $ on $ L $ so that $ S $ can be represented as $ x \rightarrow x + \alpha $ $ \mathop{\rm mod} 1 $. (If $ S $ is of class $ C ^ {1} $, this is not necessarily true [2].) The partition of the torus into trajectories will then be the same, up to a homeomorphism, as in the case described by (1) (except for the velocity of motion along the trajectories). The smoothness of the coordinate change, which is ensured by Denjoy's theorem, will depend (in addition to the smoothness of $ S $) on the arithmetical properties of the rotation number $ \alpha $. For almost-all $ \alpha $ it follows from $ S \in C ^ {n} $, $ n \geq 3 $, that the coordinate change belongs to the class $ C ^ {n-} 2 $[9], but such a change need not be smooth for rotation numbers which can be very rapidly approximated by rational numbers, even if the transformation $ S $ is analytic [7].
If the original flow on $ T ^ {2} $ has an integral invariant, a Kneser ring cannot exist, and $ S $ is smoothly conjugate to a rotation of the circle, irrespective of whether $ \alpha $ is rational or irrational. Thus, in the absence of equilibrium positions there exist on the torus cyclic coordinates $ x , y $ of the same smoothness class as the flow itself, and the form of the flow in these coordinates becomes
$$ \tag{2 } \dot{x} = f ( x , y ) ,\ \dot{y} = \alpha f ( x , y ) ,\ f ( x ,\ y ) > 0 $$
(where $ \alpha $ is the rotation number corresponding to the closed transversal $ x = \textrm{ const } $). If $ f $ is sufficiently smooth and if $ \alpha $ displays suitable properties, the flow (2) can be reduced to (1) (with $ n = 2 $ and $ \omega = ( 1 , \alpha ) $) with the aid of some diffeomorphism, but in the general case this is not always possible, and even ergodic properties of the flow (2) may differ from those of the flows (1) (a continuous spectrum is possible, but mixing is not possible in the smooth case). See [10]; the missing proofs are produced in [11], [12], [13], [15].
References
| [1] | H. Poincaré, "Mémoire sur les courbes définiés par une équation différentielle" J. Math. Pures Appl. , 1 (1885) pp. 167–244 (Also: Oeuvres, Vol.1) |
| [2] | A. Denjoy, "Sur les courbes définies par les équations différentielles à la surface du tore" J. Math. Pures Appl. (9) , 11 : 4 (1932) pp. 333–375 |
| [3] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17 |
| [4] | H. Kneser, "Reguläre Kurvenscharen auf Ringflächen" Math. Ann. , 91 : 1–2 (1924) pp. 135–154 |
| [5] | B.L. Reinhart, "Line elements on the torus" Amer. J. Math. , 81 : 3 (1959) pp. 617–631 |
| [6] | A. Aepply, L. Markus, "Integral equivalence of vector fields on manifolds and bifurcation of differential systems" Amer. J. Math. , 85 : 4 (1963) pp. 633–654 |
| [7] | V.I. Arnol'd, "Small denominators I. On maps of the circumference onto itself" Transl. Amer. Math. Soc. , 46 (1965) pp. 213–284 Izv. Akad. Nauk SSSR Ser. Mat. , 25 : 1 (1961) pp. 21–86 |
| [8] | V.I. Arnol'd, "On a theorem by Liouville concerning integrable problems" Sibirsk. Mat. Zh. , 4 : 2 (1963) pp. 471–474 (In Russian) |
| [9] | M.R. Herman, "Conjugaison 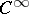 des diffeomorphismes du cercle pour presque tout nombre de rotation" C.R. Acad. Sci. , 283 : 8 (1976) pp. 579–582 des diffeomorphismes du cercle pour presque tout nombre de rotation" C.R. Acad. Sci. , 283 : 8 (1976) pp. 579–582 |
| [10] | A.N. Kolmogorov, "On dynamical systems with an integral invariant on the torus" Dokl. Akad. Nauk SSSR , 93 : 5 (1953) pp. 763–766 (In Russian) |
| [11] | S. Sternberg, "On differential equations on the torus" Amer. J. Math. , 79 : 2 (1957) pp. 397–402 |
| [12] | M.D. Shklover, "Classical dynamical systems on the torus with continuous spectrum" Izv. Vyssh. Uchebn. Zaved. Mat. , 10 (1967) pp. 113–124 (In Russian) |
| [13] | A.V. Kochergin, "On the absence of mixing in special flows over the rotation of a circle and in flows on a two-dimensional torus" Soviet Math. Dokl. , 13 (1972) pp. 949–952 Dokl. Akad. Nauk SSSR , 205 : 3 (1972) pp. 515–518 |
| [14] | S. Schwartzman, "Asymptotic cycles" Ann. of Math. , 66 : 2 (1957) pp. 270–284 |
| [15] | D.V. Anosov, "On an additive functional homology equation connected with an ergodic rotation of the circle" Math. USSR-Izv. , 7 : 6 (1973) pp. 1257–1271 Izv. Akad. Nauk. SSSR , 37 : 6 (1973) pp. 1259–1273 |
Comments
Instead of [8] (the existence of invariant tori for integrable Hamiltonian systems) one may also consult § 49 in [a1]. As to the appearance of flows on tori one may add the fact that every compact minimal subset of a $ C ^ {2} $- flow on a two-dimensional manifold is either a point, a periodic orbit or equal to the full manifold, in which case the manifold is homeomorphic to a torus; see [a5].
A good introduction into the classical theory of flows on tori can be found in [a3]. Instead of [7] and [9] (smoothness of coordinate transformation) one may consult [a4]. For the results concerning flows with an integral invariant (including the results of [10] and [12]), see Chapt. 16 of [a2].
References
| [a1] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) |
| [a2] | I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian) |
| [a3] | C. Godbillon, "Dynamical systems on surfaces" , Springer (1983) (Translated from French) |
| [a4] | M.R. Herman, "Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations" Publ. Math. IHES , 49 (1979) pp. 5–234 |
| [a5] | A.J. Schwartz, "A generalization of a Poincaré–Bendixson theorem to closed two dimensional manifolds" Amer. J. Math. , 85 (1963) pp. 453–458 |
Differential equations on a torus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_equations_on_a_torus&oldid=46682