Differential equation, partial, discontinuous initial (boundary) conditions
A problem involving partial differential equations in which the functions specifying the initial (boundary) conditions are not continuous.
For instance, consider the second-order hyperbolic equation
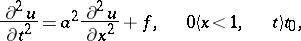 |
and pose for it the mixed problem with initial conditions
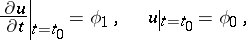 |
and boundary conditions
 |
In this case the discontinuities of the initial functions 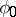 and
and 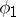 entail discontinuities of
entail discontinuities of  and
and 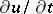 along the characteristic rays
along the characteristic rays  and
and 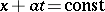 , and the measure of discontinuity
, and the measure of discontinuity
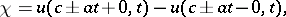 |
or
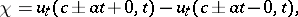 |
where 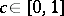 is a discontinuity point of the function
is a discontinuity point of the function 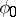 or
or 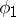 , satisfies the equation
, satisfies the equation
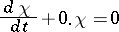 |
along the characteristic ray, i.e. 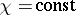 . Similar results are valid for second-order hyperbolic equations with variable coefficients:
. Similar results are valid for second-order hyperbolic equations with variable coefficients:
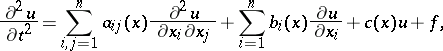 |
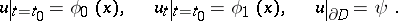 |
In this case the discontinuities of the initial functions and the boundary conditions also entail discontinuities in  and
and  along characteristic rays, which can be determined from the systems of equations
along characteristic rays, which can be determined from the systems of equations
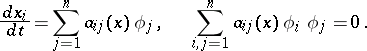 |
The measure of discontinuity 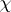 satisfies the equation:
satisfies the equation:
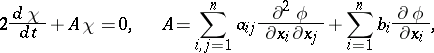 |
where the function 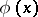 defines the characteristic surface in the form of the equation
defines the characteristic surface in the form of the equation 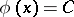 .
.
In the case of equations of elliptic type the discontinuities of the boundary conditions do not propagate inside 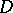 because in this case the characteristic rays are complex. For equations of elliptic type studies were made of the existence and uniqueness of the solution, and of the solution satisfying the boundary conditions. Thus, it has been proved for second-order elliptic equations in an arbitrary domain,
because in this case the characteristic rays are complex. For equations of elliptic type studies were made of the existence and uniqueness of the solution, and of the solution satisfying the boundary conditions. Thus, it has been proved for second-order elliptic equations in an arbitrary domain,
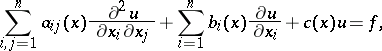 |
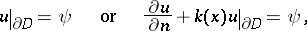 |
that if the boundary function 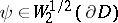 for the first boundary condition and
for the first boundary condition and 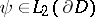 for the second boundary condition, then there exists a generalized solution in
for the second boundary condition, then there exists a generalized solution in 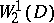 which satisfies the boundary condition on the average, i.e.
which satisfies the boundary condition on the average, i.e. 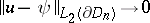 , where the surfaces
, where the surfaces 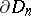 approximate the surface
approximate the surface 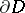 . In the case of parabolic (and also elliptic) equations, the discontinuities do not propagate inside
. In the case of parabolic (and also elliptic) equations, the discontinuities do not propagate inside 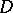 if discontinuities are present in the initial or in the boundary conditions. Problems of the existence and uniqueness of a generalized solution to the boundary condition have also been studied for these problems.
if discontinuities are present in the initial or in the boundary conditions. Problems of the existence and uniqueness of a generalized solution to the boundary condition have also been studied for these problems.
References
| [1] | A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [2] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) |
| [3] | A.V. Bitsadze, "Equations of mathematical physics" , MIR (1980) (Translated from Russian) |
| [4] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
| [5] | L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1964) |
| [6] | O.A. Ladyzhenskaya, N.N. Ural'tseva, "Linear and quasilinear elliptic equations" , Acad. Press (1968) (Translated from Russian) |
| [7] | O.A. Ladyzhenskaya, V.A. Solonnikov, N.N. Ural'tseva, "Linear and quasilinear parabolic equations" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [8] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) |
| [9] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
| [10] | S. Agmon, A. Douglis, L. Nirenberg, "Estimates near the boundary for solutions of elliptic equations" Comm. Pure Appl. Math. , 12 (1959) pp. 623–727 |
Comments
Far-reaching results have been obtained recently concerning harmonic analysis of singularities and propagation of singularities, cf. [a1].
References
| [a1] | L.V. Hörmander, "The analysis of linear partial differential operators" , 3 , Springer (1985) |
Differential equation, partial, discontinuous initial (boundary) conditions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_equation,_partial,_discontinuous_initial_(boundary)_conditions&oldid=11237