Difference between revisions of "Differential equation, partial, complex-variable methods"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | d0319301.png | ||
| + | $#A+1 = 291 n = 2 | ||
| + | $#C+1 = 291 : ~/encyclopedia/old_files/data/D031/D.0301930 Differential equation, partial, complex\AAhvariable methods | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
Methods for solving elliptic partial differential equations involving the representation of solutions by way of analytic functions of a complex variable. | Methods for solving elliptic partial differential equations involving the representation of solutions by way of analytic functions of a complex variable. | ||
The theory of analytic functions | The theory of analytic functions | ||
| − | + | $$ | |
| + | w ( z) = u ( x , y ) + i v ( x , y ) | ||
| + | $$ | ||
| − | of the complex variable | + | of the complex variable $ z = x + iy $ |
| + | is the theory of two real-valued functions $ u ( x , y ) $ | ||
| + | and $ v ( x , y ) $ | ||
| + | satisfying the Cauchy–Riemann system of equations $ u _ {x} - v _ {y} = 0 $, | ||
| + | $ u _ {y} + v _ {x} = 0 $, | ||
| + | which is essentially equivalent to the Laplace equation | ||
| − | + | $$ | |
| + | \Delta u \equiv u _ {xx} + u _ {yy} = 0 . | ||
| + | $$ | ||
Since the 1930s, methods of analytic function theory have been used to an increasing extent in the general theory of equations of elliptic type. Thus arose a new branch of analysis, a substantial extension of the classical theory of analytic functions and their applications. The main subject of this branch are representation formulas for all solutions of a very extensive class of equations of elliptic type by analytic functions of one complex variable. For linear equations these representations are realized using certain linear operators, expressed in terms of the coefficients of the equations. These formulas make it possible to extend the properties of analytic functions to solutions of an equation of elliptic type, and important properties such as the uniqueness theorem, the principle of the argument, Liouville's theorem, etc., are often literally preserved. Taylor and Laurent series, the Cauchy integral formula, the compactness principle, the principle of analytic continuation, etc., are extended in a natural way. | Since the 1930s, methods of analytic function theory have been used to an increasing extent in the general theory of equations of elliptic type. Thus arose a new branch of analysis, a substantial extension of the classical theory of analytic functions and their applications. The main subject of this branch are representation formulas for all solutions of a very extensive class of equations of elliptic type by analytic functions of one complex variable. For linear equations these representations are realized using certain linear operators, expressed in terms of the coefficients of the equations. These formulas make it possible to extend the properties of analytic functions to solutions of an equation of elliptic type, and important properties such as the uniqueness theorem, the principle of the argument, Liouville's theorem, etc., are often literally preserved. Taylor and Laurent series, the Cauchy integral formula, the compactness principle, the principle of analytic continuation, etc., are extended in a natural way. | ||
| Line 16: | Line 37: | ||
Let the second-order equation of elliptic type | Let the second-order equation of elliptic type | ||
| − | + | $$ \tag{1 } | |
| + | \Delta u + a ( x , y ) | ||
| + | \frac{\partial u }{\partial x } | ||
| + | + b | ||
| + | ( x , y ) | ||
| + | \frac{\partial u }{\partial y } | ||
| + | + c ( x , y ) u = 0 | ||
| + | $$ | ||
| + | |||
| + | be given, where $ a $, | ||
| + | $ b $ | ||
| + | and $ c $ | ||
| + | are analytic functions in the real variables $ x $ | ||
| + | and $ y $ | ||
| + | in some domain of the $ z $- | ||
| + | plane, $ z = x + iy $. | ||
| + | Analytic continuation of the coefficients into the domain of the independent complex variables $ z = x + iy $, | ||
| + | $ \zeta = x - iy $ | ||
| + | yields the following form of equation (1): | ||
| + | |||
| + | $$ \tag{2 } | ||
| − | + | \frac{\partial ^ {2} u }{\partial z \partial \zeta } | |
| + | + A ( z , \zeta ) | ||
| − | + | \frac{\partial u }{\partial z } | |
| + | + B ( z , \zeta ) | ||
| + | \frac{\partial u }{\partial | ||
| + | \zeta } | ||
| + | + C ( z , \zeta ) u = 0 . | ||
| + | $$ | ||
| − | A simply-connected domain | + | A simply-connected domain $ D _ {0} $ |
| + | is said to be a fundamental domain for equation (1) if $ A $, | ||
| + | $ B $ | ||
| + | and $ C $ | ||
| + | are analytic functions of two independent variables in the cylindrical domain $ ( D _ {0} , {\overline{D}\; } _ {0} ) $, | ||
| + | where $ {\overline{D}\; } _ {0} $ | ||
| + | denotes the mirror image of $ D _ {0} $ | ||
| + | with respect to the real axis. | ||
| − | If | + | If $ D \subset D _ {0} $ |
| + | is a simply-connected domain, all solutions of equation (1) regular in the domain $ D $ | ||
| + | are expressed by the formula | ||
| − | + | $$ \tag{3 } | |
| + | u ( x , y ) = \mathop{\rm Re} \left \{ G ( z , z _ {0} ; z , z | ||
| + | bar ) \Phi ( z) \right . - | ||
| + | $$ | ||
| − | + | $$ | |
| + | - \left . | ||
| + | \int\limits _ {z _ {1} } ^ { z } \Phi ( t) | ||
| + | \frac \partial { | ||
| + | \partial t } | ||
| + | G ( t , {\overline{z}\; } _ {0} , z , \overline{z}\; ) d t \right \} , | ||
| + | $$ | ||
| − | where | + | where $ \Phi ( z) $ |
| + | is an arbitrary holomorphic function in $ D $, | ||
| + | $ z _ {1} , z _ {0} \in D $ | ||
| + | are arbitrary fixed points; the analytic function $ G ( z , \zeta ; y , \tau ) $ | ||
| + | of four independent complex arguments in the cylindrical domain $ ( D _ {0} , {\overline{D}\; } _ {0} , D _ {0} , {\overline{D}\; } _ {0} ) $ | ||
| + | is said to be the Riemann function of equation (1). It is the solution of the integral equation of Volterra type: | ||
| − | + | $$ \tag{4 } | |
| + | G ( z , \zeta ; t , \tau ) - \int\limits _ \tau ^ \zeta A ( z , \eta ,\ | ||
| + | t , \tau ) d \eta + | ||
| + | $$ | ||
| − | + | $$ | |
| + | - \int\limits _ { t } ^ { z } B ( \xi , \zeta ) G ( \xi , \zeta ; t , \tau ) d \xi + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | \int\limits _ { t } ^ { z } d \xi \int\limits _ \tau ^ \zeta C ( \xi , \eta | ||
| + | ) G ( \xi , \eta ; t , \tau ) d \eta = 1 . | ||
| + | $$ | ||
| − | The correspondence between the family of solutions | + | The correspondence between the family of solutions $ \{ u \} $ |
| + | of equation (1) and the family of holomorphic functions $ \{ \Phi \} $ | ||
| + | produced by formula (3) will be a one-to-one correspondence if the values of the imaginary parts of $ \Phi $ | ||
| + | are fixed in a given point $ z _ {1} $ | ||
| + | of $ D $. | ||
| + | If $ z _ {1} = z _ {0} = 0 $, | ||
| + | the inversion formula | ||
| − | + | $$ | |
| + | \Phi ( z) = 2 u \left ( | ||
| + | \frac{z}{2} | ||
| + | , | ||
| + | \frac{z}{2i} | ||
| + | \right ) - u | ||
| + | ( 0 , 0 ) G ( 0 , 0 ; z , 0 ) | ||
| + | $$ | ||
is valid. Equation (4) can be solved by the method of successive approximation. An approximate expression of the Riemann function can be obtained in this way. | is valid. Equation (4) can be solved by the method of successive approximation. An approximate expression of the Riemann function can be obtained in this way. | ||
| − | If the domain | + | If the domain $ D $ |
| + | is multiply connected, formula (3) usually gives multi-valued solutions. In order to obtain all single-valued solutions of equation (1) in this case, multi-valued functions of a certain type must be taken for $ \Phi $ | ||
| + | in (3). | ||
| − | Let | + | Let $ D $ |
| + | be a doubly-connected domain $ ( D \subset D _ {0} ) $; | ||
| + | let $ D ^ \prime $ | ||
| + | be a bounded continuum completing $ D $ | ||
| + | to a simply-connected domain. All solutions of equation (1) which are single-valued in $ D $ | ||
| + | are then given by the formula | ||
| − | + | $$ \tag{5 } | |
| + | u ( x , y ) = \mathop{\rm Re} \left \{ G ( z , {\overline{z}\; } _ {0} ; z ,\ | ||
| + | \overline{z}\; ) \Phi ( z) \right . - | ||
| + | $$ | ||
| − | + | $$ | |
| + | - \left . | ||
| + | \int\limits _ {z _ {1} } ^ { z } \Phi ( t) H ( t ,\ | ||
| + | {\overline{z}\; } _ {0} , z , \overline{z}\; ) d t \right \} , | ||
| + | $$ | ||
| − | where | + | where $ z _ {1} \in D $, |
| + | $ z _ {0} \in D ^ \prime $ | ||
| + | are fixed points, and $ \Phi ( z) $ | ||
| + | is a multi-valued analytic function of the form | ||
| − | + | $$ | |
| + | \Phi ( z) = \Phi _ {0} ( z) + \left [ \alpha G ( z _ {0} , {\overline{z}\; } _ {0} ; z , \overline{z}\; ) \right . - | ||
| + | $$ | ||
| − | + | $$ | |
| + | - \left . | ||
| − | + | \frac{1}{2 \pi i } | |
| + | \int\limits _ { L } \overline{ {\Phi _ {0} ( t) }}\; H ^ {*} ( z _ {0} , t , z , {\overline{z}\; } _ {0} ) dt \right ] \mathop{\rm ln} ( z - z _ {0} ) . | ||
| + | $$ | ||
| − | + | Here, $ \alpha $ | |
| + | is an arbitrary real constant, $ \Phi _ {0} ( z) $ | ||
| + | is an arbitrary holomorphic function in $ D $, | ||
| + | and $ L $ | ||
| + | is any simple, closed, piecewise-smooth curve lying in $ D $ | ||
| + | and enclosing $ D ^ \prime $. | ||
| + | The functions $ H $ | ||
| + | and $ H ^ {*} $ | ||
| + | are expressed by the formulas | ||
| − | + | $$ | |
| + | H ( t , \tau , z , \zeta ) = | ||
| + | \frac \partial {\partial t } | ||
| + | G | ||
| + | ( t , \tau ; z , \zeta ) - B ( t , \tau ) G ( t , \tau ; z , | ||
| + | \zeta ) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | H ^ {*} ( t , \tau , z , \zeta ) = | ||
| + | \frac \partial {\partial \tau } | ||
| + | G ( t , | ||
| + | \tau ; z , \zeta ) - A ( t , \tau ) G ( t , \tau ; z , \zeta ) . | ||
| + | $$ | ||
| − | + | Complex representations of the type (3) are also extended to a system of equations written in a vector form (1), where $ u $ | |
| + | is a vector with components $ u _ {1} \dots u _ {n} $, | ||
| + | and $ a , b , c $ | ||
| + | are square matrices of order $ n $ | ||
| + | whose entries are analytic functions of the variables $ x , y $. | ||
| − | + | In a domain in which there is at least one positive solution $ u _ {0} > 0 $ | |
| + | for (1), equation (1) may be converted to the form | ||
| − | + | $$ | |
| + | \Delta v + a v _ {x} + b v _ {y} = 0 | ||
| + | $$ | ||
| − | + | by substituting $ u= u _ {0} v $. | |
| + | (Such a solution always exists in a small neighbourhood of any fixed point, and also in any domain where $ c \leq 0 $.) | ||
| + | In this case equation (1) is equivalent to the system of equations | ||
| − | + | $$ \tag{6 } | |
| + | u _ {x} - v _ {y} + a u + b v = 0 ,\ \ | ||
| + | u _ {y} + v _ {x} + c u + d v = 0 , | ||
| + | $$ | ||
| − | + | which is a special case of the generalized Cauchy–Riemann system. Introducing the complex function $ w = u + i v $, | |
| + | the system may be written as | ||
| − | + | $$ \tag{7 } | |
| + | \partial _ {\overline{z}\; } w + A ( z) w + B ( z) \overline{w}\; = 0 ,\ \ | ||
| + | 2 \partial _ {\overline{z}\; } = \partial _ {x} + i \partial _ {y} . | ||
| + | $$ | ||
| − | + | If the coefficients $ A $ | |
| + | and $ B $ | ||
| + | are analytic functions of the complex arguments $ z $ | ||
| + | and $ \zeta $( | ||
| + | $ z = x + i y $, | ||
| + | $ \zeta = x - i y $) | ||
| + | in some cylindrical domain $ ( D _ {0} , {\overline{D}\; } _ {0} ) $, | ||
| + | where $ D _ {0} $ | ||
| + | is a simply-connected domain, then the solution of equation (7) in a simply-connected domain $ D \subset D _ {0} $ | ||
| + | is given by the formula: | ||
| − | + | $$ \tag{8 } | |
| + | w ( z) = \mathop{\rm exp} \left \{ \int\limits _ {z _ {0} } ^ { z } A ( z ,\ | ||
| + | \tau ) d \tau \right \} \times | ||
| + | $$ | ||
| − | + | $$ | |
| + | \times | ||
| + | \left \{ \Phi ( z) + \int\limits _ {z _ {0} } ^ { z } {\widetilde \Gamma } _ {1} ( z , \overline{z}\; , t ) \Phi ( t) d t + \int\limits _ | ||
| + | { {\overline{z}\; } _ {0} } ^ { {z } bar } {\widetilde \Gamma } _ {2} ( | ||
| + | z , \overline{z}\; , t ) \Phi ( t) d t \right \} , | ||
| + | $$ | ||
| − | If | + | where $ {\widetilde \Gamma } _ {1} $ |
| + | and $ {\widetilde \Gamma } _ {2} $ | ||
| + | are analytic functions of their arguments, defined in terms of $ A $ | ||
| + | and $ B $ | ||
| + | and constructed by the method of successive approximation; $ \Phi $ | ||
| + | is an arbitrary analytic function of the variable $ z $. | ||
| + | |||
| + | If $ A $ | ||
| + | and $ B $ | ||
| + | are entire functions of the variables $ x $ | ||
| + | and $ y $, | ||
| + | the representation (8) is valid for any simply-connected domain of the $ z $- | ||
| + | plane, irrespective of the behaviour of the coefficients $ A $ | ||
| + | and $ B $ | ||
| + | near infinity. | ||
Let the elliptic equation | Let the elliptic equation | ||
| − | + | $$ \tag{9 } | |
| + | \Delta ^ {n} u + \sum _ {k = 1 } ^ { n } \sum _ {0 \leq p + q | ||
| + | \leq k } a _ {p , q } ^ {( k) } | ||
| + | \frac{\partial ^ {p+} q \Delta ^ {n-} k u | ||
| + | }{\partial x ^ {p} \partial y ^ {q} } | ||
| + | = 0 | ||
| + | $$ | ||
| − | be given, where | + | be given, where $ a _ {p,q} ^ {( k) } $ |
| + | are analytic functions of $ x $ | ||
| + | and $ y $. | ||
| + | If $ D _ {0} $ | ||
| + | is a fundamental domain for equation (9), any regular solution of this equation in a simply-connected domain $ D \subset D _ {0} $ | ||
| + | is expressed by the formula | ||
| − | + | $$ \tag{10 } | |
| + | u ( x , y ) = \mathop{\rm Re} \left \{ G ( z , z _ {0} ; z , z | ||
| + | bar ) \Phi _ {0} ( z) \right . - | ||
| + | $$ | ||
| − | + | $$ | |
| + | - \left . | ||
| + | \sum _ {k = 0 } ^ { n- } 1 \int\limits _ {z _ {1} } ^ { z } \Phi _ {k} ( t) | ||
| + | \frac \partial {\partial t } | ||
| + | G _ {k} ( t , {z | ||
| + | bar } _ {0} ; z , \overline{z}\; ) d t \right \} , | ||
| + | $$ | ||
| − | where | + | where $ \Phi _ {0} \dots \Phi _ {n-} 1 $ |
| + | are arbitrary functions holomorphic in $ D $, | ||
| + | and | ||
| − | + | $$ | |
| + | G _ {k} ( t , \tau ; z , \zeta ) = | ||
| + | \frac{\partial ^ {2 ( n - k - 1 | ||
| + | ) } G ( t , \tau ; z , \zeta ) }{\partial t ^ {n-} k- 1 \partial \tau | ||
| + | ^ {n-} k- 1 } | ||
| + | ,\ k = 0 \dots n - 1 . | ||
| + | $$ | ||
| − | Here | + | Here $ G $ |
| + | is the complex Riemann function of equation (9) which depends analytically on the complex arguments $ ( t , \tau , z , \zeta ) $ | ||
| + | in the cylindrical domain $ ( D _ {0} , {\overline{D}\; } _ {0} , D _ {0} , {\overline{D}\; } _ {0} ) $. | ||
| + | If the conditions | ||
| − | + | $$ | |
| + | \Phi _ {k} ( z _ {1} ) = \overline{ {\Phi _ {k} ( z _ {1} ) }}\; , | ||
| + | \ k = 0 \dots n - 1 , | ||
| + | $$ | ||
| − | are satisfied, formula (10) realizes a one-to-one correspondence between the family of solutions | + | are satisfied, formula (10) realizes a one-to-one correspondence between the family of solutions $ \{ u \} $ |
| + | of equation (9) and the family of holomorphic functions $ \{ ( \Phi _ {0} \dots \Phi _ {n-} 1 ) \} $. | ||
| + | If $ D $ | ||
| + | is a multiply-connected domain, formula (10) usually yields multi-valued solutions. However, as for equations of the second order, the formula may be modified so that it yields all single-valued solutions of equation (9) in a multiply-connected domain as well. Formula (10) may also be extended to a system of equations such as (9), where $ u $ | ||
| + | is a vector and the coefficients are matrices. | ||
For several equations of mathematical physics the Riemann function is explicitly given using elementary or special functions. | For several equations of mathematical physics the Riemann function is explicitly given using elementary or special functions. | ||
| Line 112: | Line 330: | ||
For the equation of the vibrating membrane, | For the equation of the vibrating membrane, | ||
| − | + | $$ | |
| + | \Delta u + \lambda ^ {2} u = 0 ,\ \lambda = \textrm{ const } , | ||
| + | $$ | ||
| − | + | $$ | |
| + | G ( z , \zeta ; t , \tau ) = J _ {0} ( \lambda \sqrt {( z - t ) ( \zeta - \tau ) } ) , | ||
| + | $$ | ||
| − | where | + | where $ J _ {0} $ |
| + | is the Bessel function of order zero, and the complex plane is taken as fundamental domain. The case $ \lambda = 0 $ | ||
| + | yields the Laplace equation $ \Delta u = 0 $; | ||
| + | then $ G = 1 $ | ||
| + | and formula (3) assumes the form | ||
| − | + | $$ | |
| + | u = \mathop{\rm Re} [ \Phi ( z) ] . | ||
| + | $$ | ||
For the equation of spherical functions, | For the equation of spherical functions, | ||
| − | + | $$ | |
| + | \Delta u + n ( n + 1 ) ( 1 + x ^ {2} + y ^ {2} ) ^ {-} 2 u = \ | ||
| + | 0 ,\ n = \textrm{ const } , | ||
| + | $$ | ||
| − | + | $$ | |
| + | G ( z , \zeta ; t , \tau ) = P _ {n} \left ( | ||
| + | \frac{( 1 - z \zeta ) ( | ||
| + | 1 - t \tau ) + 2 z \tau + 2 \zeta t }{( 1 + z \zeta ) ( 1 + t \tau ) } | ||
| + | \right ) , | ||
| + | $$ | ||
| − | where | + | where $ P _ {n} $ |
| + | is the Legendre function of the first kind; any simply-connected domain $ D _ {0} $ | ||
| + | which satisfies the condition: if $ z \in D _ {0} $, | ||
| + | $ \zeta \in D _ {0} $, | ||
| + | then $ z \zeta \neq 1 $( | ||
| + | e.g. the disc $ | z | < 1 $), | ||
| + | may be taken as fundamental domain. In the case of the Euler–Darboux equation | ||
| − | + | $$ | |
| + | \Delta u + y ^ {-} 1 ( \alpha u _ {x} + \alpha ^ \prime u _ {y} ) = \ | ||
| + | 0 ,\ \alpha , \alpha ^ \prime = \textrm{ const } , | ||
| + | $$ | ||
| − | + | $$ | |
| + | G ( z , \zeta ; t , \tau ) = ( \tau - z ) ^ {- \beta ^ \prime | ||
| + | } ( \zeta - t ) ^ {- \beta } ( \zeta - z ) ^ {\beta + \beta ^ \prime } \times | ||
| + | $$ | ||
| − | + | $$ | |
| + | \times | ||
| + | F \left ( \beta ^ \prime , \beta , 1 , | ||
| + | \frac{( z - t ) ( | ||
| + | \zeta - \tau ) }{( z - t ) ( \zeta - t ) } | ||
| + | \right ) , | ||
| + | $$ | ||
| − | where | + | where $ 2 \beta = \alpha ^ \prime + i \alpha $, |
| + | $ 2 \beta ^ \prime = \alpha ^ \prime - i \alpha $, | ||
| + | and $ F $ | ||
| + | is the hypergeometric series; the half-planes $ y > 0 $ | ||
| + | or $ y < 0 $ | ||
| + | may be taken as fundamental domains. | ||
For the equation | For the equation | ||
| − | + | $$ | |
| + | \Delta ^ {n} u = 0 ,\ n = 1 , 2 \dots | ||
| + | $$ | ||
| − | + | $$ | |
| + | G ( z , \zeta ; t , \tau ) = | ||
| + | \frac{( z - 1 ) ^ {n-} 1 ( | ||
| + | \zeta - t ) ^ {n-} 1 }{( n - 1 ) ! ( n - 1 ) ! } | ||
| + | , | ||
| + | $$ | ||
Goursat's formula | Goursat's formula | ||
| − | + | $$ | |
| + | u = \mathop{\rm Re} [ ( z \overline{z}\; ) ^ {n-} 1 \Phi _ {n-} 1 + ( z \overline{z}\; ) | ||
| + | ^ {n-} 2 \Phi _ {n-} 2 + \dots + \Phi _ {0} ] | ||
| + | $$ | ||
is valid. | is valid. | ||
| Line 150: | Line 419: | ||
The method of complex representation of solutions is also applicable to a certain class of non-linear equations. For instance, let the Gauss equation | The method of complex representation of solutions is also applicable to a certain class of non-linear equations. For instance, let the Gauss equation | ||
| − | + | $$ | |
| + | \Delta u = - 2 k e ^ {u} | ||
| + | $$ | ||
| − | be given, where | + | be given, where $ k ( x , y ) $ |
| + | is a given function (this is a well-known equation in differential geometry). If $ v _ {0} ( z) $ | ||
| + | is any particular solution of this equation, the functions of the type | ||
| − | + | $$ | |
| + | u ( z) = v _ {0} [ \Phi ( z) ] | \Phi ^ \prime ( z) | ^ {2} , | ||
| + | $$ | ||
| − | where | + | where $ \Phi ( z) $ |
| + | is an arbitrary analytic function, are also solutions. If $ k = \textrm{ const } $, | ||
| + | then $ v _ {0} = 4 ( 1 - k z \overline{z}\; ) ^ {-} 2 $ | ||
| + | and all solutions of the Gauss equation may be expressed by the formula: | ||
| − | + | $$ | |
| + | u ( x , y ) = 4 | \Phi ^ \prime ( z) | ^ {2} ( 1 + k | \Phi | ||
| + | ( z) | ^ {2} ) ^ {-} 2 . | ||
| + | $$ | ||
| − | If < | + | If $ k < 0 $, |
| + | it should be assumed that $ | \Phi ( z) | < - k ^ {-} 1 $. | ||
==Elliptic equations with non-analytic coefficients.== | ==Elliptic equations with non-analytic coefficients.== | ||
| − | Let there be given a generalized system of Cauchy–Riemann equations (7) with coefficients | + | Let there be given a generalized system of Cauchy–Riemann equations (7) with coefficients $ A $ |
| + | and $ B $ | ||
| + | defined on the whole complex $ z $- | ||
| + | plane $ E $ | ||
| + | and belonging to the class $ L _ {p,2} ( E) $, | ||
| + | i.e. | ||
| + | |||
| + | $$ | ||
| + | A ( z) , B ( z) \in L _ {p} ,\ | z | ^ {-} 2 A \left ( | ||
| + | \frac{1}{z} | ||
| − | + | \right ) , | z | ^ {-} 2 B \left ( | |
| + | \frac{1}{z} | ||
| + | \right ) \in \ | ||
| + | L _ {p} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | p > 2 ,\ | z | \leq 1 . | ||
| + | $$ | ||
| − | If the coefficients are given in a bounded domain | + | If the coefficients are given in a bounded domain $ S $ |
| + | and belong to the class $ L _ {p} ( S) $, | ||
| + | $ p > 2 $, | ||
| + | they will satisfy the above conditions when extended by zero outside $ S $. | ||
| + | Under these assumptions, equation (7) usually has no solutions in the classical sense. One accordingly considers a so-called generalized solution: A function $ w ( z) \in L _ {1} ( S) $ | ||
| + | is called a solution of equation (7) in $ S $ | ||
| + | if it has a derivative in the generalized sense (as defined by S.L. Sobolev) $ \partial _ {\overline{z}\; } w \in L _ {1} ( S) $ | ||
| + | and satisfies the equation almost-everywhere in $ S $. | ||
| − | The theory of functions satisfying equation (7) is a far-reaching generalization of the classical theory of analytic functions | + | The theory of functions satisfying equation (7) is a far-reaching generalization of the classical theory of analytic functions $ ( A \equiv B \equiv 0 ) $ |
| + | and retains their principal features. For this reason solutions of equations of the type (7) are known as generalized analytic functions (cf. [[Generalized analytic function|Generalized analytic function]]). | ||
| − | Any solution of equation (7) (in | + | Any solution of equation (7) (in $ S $) |
| + | satisfies the integral equation | ||
| − | + | $$ \tag{11 } | |
| + | w ( z) - | ||
| + | \frac{1} \pi | ||
| + | {\int\limits \int\limits } _ { S } | ||
| + | \frac{A ( \zeta ) w ( \zeta ) + B ( \zeta ) | ||
| + | \overline{ {w ( \zeta ) }}\; }{\zeta - z } | ||
| + | d \xi d \eta = \Phi ( z) , | ||
| + | $$ | ||
| − | where | + | where $ \zeta = \xi + i \eta $ |
| + | and $ \Phi ( z) $ | ||
| + | is a holomorphic function in $ S $. | ||
| + | If $ \Phi \in L _ {q} ( \overline{S}\; ) $, | ||
| + | $ q \geq p / ( p - 1 ) $, | ||
| + | $ p > 2 $, | ||
| + | equation (11) has a unique solution, which is expressed by the formula | ||
| − | + | $$ \tag{12 } | |
| + | w ( z) = \Phi ( z) + {\int\limits \int\limits } _ { S } \Gamma _ {1} ( z , \zeta ) \Phi ( | ||
| + | \zeta ) d \xi d \eta + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | {\int\limits \int\limits } _ { S } \Gamma _ {2} ( z , \zeta ) \overline{ {\Phi ( \zeta ) }}\; d \xi d \eta . | ||
| + | $$ | ||
| − | The resolvents | + | The resolvents $ \Gamma _ {1} $ |
| + | and $ \Gamma _ {2} $ | ||
| + | depend on the coefficients of equation (7) and are constructed by the method of successive approximation. | ||
| − | Formula (12) gives a general (linear) representation of solutions of (7) by analytic functions | + | Formula (12) gives a general (linear) representation of solutions of (7) by analytic functions $ \Phi ( z) $. |
| + | In particular, it permits the construction of the so-called fundamental kernels | ||
| − | + | $$ | |
| + | \Omega _ {1} ( z , t ) = X _ {1} ( z , t ) + i X _ {2} ( z , t) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \Omega _ {2} ( z , t ) = X _ {1} ( z , t ) - i X _ {2} ( z , t ), | ||
| + | $$ | ||
| − | where | + | where $ t $ |
| + | is some fixed point, and $ X _ {1} $ | ||
| + | and $ X _ {2} $ | ||
| + | are solutions of the integral equation (11) corresponding to the functions | ||
| − | + | $$ | |
| + | 2 \Phi _ {1} = ( t - z ) ^ {-} 1 ,\ 2 i \Phi _ {2} = ( t - z ) ^ {-} 1 . | ||
| + | $$ | ||
These kernels permit one to state the generalized Cauchy formula: | These kernels permit one to state the generalized Cauchy formula: | ||
| − | + | $$ \tag{13 } | |
| + | |||
| + | \frac{1}{2 \pi i } | ||
| + | \int\limits _ {\partial S } \Omega _ {1} ( z , \zeta ) w ( | ||
| + | \zeta ) d \zeta - \Omega _ {2} ( z , \zeta ) \overline{ {w ( \zeta ) }}\; d \zeta | ||
| + | bar = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | \left \{ | ||
| + | \begin{array}{ll} | ||
| + | w ( z) , & z \in S , \\ | ||
| + | w( | ||
| + | \frac{z)}{2} | ||
| + | , & z \in \partial S , \\ | ||
| + | 0 , & z \notin \overline{S}\; . \\ | ||
| + | \end{array} | ||
| − | If | + | \right .$$ |
| + | |||
| + | If $ A \equiv B \equiv 0 $, | ||
| + | this formula becomes the classical Cauchy formula. Formula (13) may serve to extend many properties of analytic functions which are usually demonstrated by the Cauchy formula to generalized analytic functions. In particular, it is possible to generalize the classical theorems on analytic continuation, to construct a theory of generalized integrals of Cauchy type to obtain representations of generalized analytic functions in the form of contour integrals with a real density, etc. | ||
The functions | The functions | ||
| − | + | $$ | |
| + | \Omega _ {1} ^ {*} ( z , t ) = - \Omega _ {1} ( t , z ) ,\ \ | ||
| + | \Omega _ {2} ^ {*} ( z , t ) = - \overline{ {\Omega _ {2} ( t , z ) }}\; | ||
| + | $$ | ||
are the fundamental kernels of the adjoint equation | are the fundamental kernels of the adjoint equation | ||
| − | + | $$ \tag{14 } | |
| + | \partial _ {\overline{z}\; } w _ {*} - A w _ {*} - \overline{ {B w _ {*} }}\; = 0 . | ||
| + | $$ | ||
| − | If, in | + | If, in $ S $, |
| + | $ w $ | ||
| + | and $ w _ {*} $ | ||
| + | satisfy the equations (7) and (14), respectively, and if they are continuous in $ \overline{S}\; $, | ||
| + | one has the identity (the analogue of the classical Cauchy theorem): | ||
| − | + | $$ | |
| + | \mathop{\rm Re} \left [ i \int\limits _ {\partial S } w ( z) w _ {*} ( z) d z \right ] = 0 . | ||
| + | $$ | ||
| − | If | + | If $ w ( z) $ |
| + | is a solution of equation (7) in the domain $ S $, | ||
| + | there exists an analytic function $ \Phi ( z) $ | ||
| + | in $ S $ | ||
| + | such that | ||
| − | + | $$ \tag{15 } | |
| + | w ( z) = \Phi ( z) e ^ {\omega ( z) } , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ \tag{16 } | |
| + | \omega ( z) = | ||
| + | \frac{1} \pi | ||
| + | {\int\limits \int\limits } _ { S } | ||
| + | \frac{A ( \zeta ) + B ( \zeta ) ( w | ||
| + | bar ( \zeta ) / w ( \zeta )) }{\zeta - z } | ||
| + | d \xi d \eta , | ||
| + | $$ | ||
| + | |||
| + | and which belongs to the class $ C _ \alpha ( E) $, | ||
| + | $ \alpha = p / ( p - 2 ) $; | ||
| + | moreover, $ \omega ( z) \rightarrow 0 $ | ||
| + | as $ z \rightarrow \infty $. | ||
| − | + | In particular, this formula permits the extension of fundamental theorems of the classical theory of analytic functions — the uniqueness theorem, Liouville's theorem, the principle of the argument, the compactness principle, etc. — to the solutions of equations such as (7). Formula (16) may be reversed: Given an analytic function $ \Phi $ | |
| + | it is possible to find a function $ w ( z) $ | ||
| + | satisfying the non-linear integral equation (16). | ||
| − | + | Let $ \Phi ( z) $ | |
| + | be an analytic function in a domain $ S $, | ||
| + | which may have arbitrary singularities, and let $ t $ | ||
| + | be a fixed point. Then there exists a solution $ w ( z) $ | ||
| + | of equation (7) such that the function $ w _ {0} = w / \Phi $ | ||
| + | is continuously extendable onto the whole plane $ E $, | ||
| + | belongs to the class $ C _ \alpha ( E) $, | ||
| + | $ \alpha = ( p - 2 ) / p $, | ||
| + | does not vanish anywhere in $ E $, | ||
| + | and $ w _ {0} ( t)= 1 $. | ||
| + | The function $ w _ {0} $ | ||
| + | satisfies the integral equation | ||
| − | + | $$ \tag{17 } | |
| + | w _ {0} ( z) - | ||
| + | \frac{z - t } \pi | ||
| + | {\int\limits \int\limits } _ { S } | ||
| − | + | \frac{A ( \zeta ) w _ {0} ( \zeta ) + B _ {0} ( \zeta ) {w _ {0} ( \zeta ) | |
| + | } bar }{( \zeta - z ) ( \zeta - t ) } | ||
| + | d \xi d \eta = 1 , | ||
| + | $$ | ||
| − | + | $$ | |
| + | B _ {0} = B | ||
| + | \frac{\overline \Phi \; } \Phi | ||
| + | , | ||
| + | $$ | ||
| − | which has a unique solution, while the function | + | which has a unique solution, while the function $ w = \Phi ( z) w _ {0} $ |
| + | satisfies the non-linear integral equation | ||
| − | + | $$ \tag{18 } | |
| + | w ( z) = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | \Phi ( z) \mathop{\rm exp} \left \{ | ||
| + | \frac{z - t } \pi | ||
| + | {\int\limits \int\limits } _ { S } | ||
| + | \frac{A ( | ||
| + | \zeta ) w ( \zeta ) + B ( \zeta ) \overline{ {w ( \zeta ) }}\; }{ | ||
| + | ( \zeta - z ) ( \zeta - t ) w } | ||
| + | d \xi d \eta \right \} , | ||
| + | $$ | ||
| − | from which, as | + | from which, as $ t \rightarrow \infty $, |
| + | the representation (15) is obtained. | ||
The problem of reducing a second-order elliptic equation of general type | The problem of reducing a second-order elliptic equation of general type | ||
| − | + | $$ \tag{19 } | |
| + | a | ||
| + | \frac{\partial ^ {2} u }{\partial x ^ {2} } | ||
| + | + 2 b | ||
| + | \frac{\partial ^ {2} u }{\partial x \partial y } | ||
| + | + c | ||
| + | \frac{\partial ^ {2} u }{\partial y ^ {2} } | ||
| + | + d | ||
| + | \frac{ | ||
| + | \partial u }{\partial x } | ||
| + | + e | ||
| + | \frac{\partial u }{\partial y } | ||
| + | + f ( u) = 0 | ||
| + | $$ | ||
to the form (1) is equivalent to the problem of reducing the positive quadratic form | to the form (1) is equivalent to the problem of reducing the positive quadratic form | ||
| − | + | $$ | |
| + | a d x ^ {2} + 2 b d x d y + c d y ^ {2} ,\ a > 0 ,\ \Delta | ||
| + | \equiv a c - b ^ {2} > 0 , | ||
| + | $$ | ||
to canonical form. This problem is equivalent to finding the homeomorphisms defined by the solution of the Beltrami equation | to canonical form. This problem is equivalent to finding the homeomorphisms defined by the solution of the Beltrami equation | ||
| − | + | $$ \tag{20 } | |
| + | \partial _ {\overline{z}\; } w - q ( z) \partial _ {z} w = 0 ,\ \ | ||
| + | w = \widetilde{x} + i \widetilde{y} , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | q ( z) = ( a - \sqrt \Delta - i b ) ( a + \sqrt \Delta + | ||
| + | i b ) ^ {-} 1 ,\ | q ( z) | < 1 . | ||
| + | $$ | ||
| − | If (19) is a uniformly elliptic equation ( | + | If (19) is a uniformly elliptic equation ( $ \Delta \geq \Delta _ {0} = \textrm{ const } > 0 $), |
| + | then $ | q ( z) | \leq q _ {0} = \textrm{ const } < 1 $. | ||
| − | The principal problem in the study of the Beltrami equation is the construction of a solution in a given domain | + | The principal problem in the study of the Beltrami equation is the construction of a solution in a given domain $ S $; |
| + | if $ \omega ( z) $ | ||
| + | is a solution of the Beltrami equation realizing a homeomorphism of the domain $ S $ | ||
| + | onto the domain $ \omega ( S) $, | ||
| + | then any other solution of the equation in $ S $ | ||
| + | has the form | ||
| − | + | $$ \tag{21 } | |
| + | w ( z) = \Phi [ \omega ( z) ] , | ||
| + | $$ | ||
| − | where | + | where $ \Phi $ |
| + | is an arbitrary analytic function in $ \omega ( S) $. | ||
| − | If | + | If $ q ( z) $ |
| + | is measurable, $ q ( z) \equiv 0 $ | ||
| + | outside $ S $ | ||
| + | and $ | q ( z) | \leq q _ {0} < 1 $, | ||
| + | the Beltrami equation has a solution of the form | ||
| − | + | $$ \tag{22 } | |
| + | w ( z) = z - | ||
| + | \frac{1} \pi | ||
| + | {\int\limits \int\limits } _ { E } | ||
| + | \frac{\rho ( \zeta ) d \xi d \eta }{\zeta - z } | ||
| + | , | ||
| + | $$ | ||
| − | where | + | where $ \rho $ |
| + | satisfies the singular integral equation | ||
| − | + | $$ \tag{23 } | |
| + | \rho ( z) - | ||
| + | \frac{q ( z) } \pi | ||
| + | {\int\limits \int\limits } _ { E } | ||
| + | \frac{\rho ( \zeta ) d \xi d \eta }{( \zeta - z ) ^ {2} } | ||
| + | = q ( z) , | ||
| + | $$ | ||
| − | in which the integral is understood in the sense of the Cauchy principal value. This equation has a unique solution in some class | + | in which the integral is understood in the sense of the Cauchy principal value. This equation has a unique solution in some class $ L _ {p} ( E) $, |
| + | $ p > 2 $, | ||
| + | and may be obtained by the method of successive approximation. The function (22) belongs to the class $ C _ \alpha ( E) $, | ||
| + | $ \alpha = p / ( p - 2 ) $, | ||
| + | realizes a homeomorphism of the plane onto itself, and $ w ( \infty ) = \infty $, | ||
| + | $ z ^ {-} 1 w ( z) \rightarrow 1 $ | ||
| + | as $ z \rightarrow \infty $. | ||
| + | If $ q \in C _ \alpha ^ {m} ( E) $, | ||
| + | $ 0 < \alpha < 1 $, | ||
| + | $ m \geq 0 $, | ||
| + | then $ w ( z) \in C _ \alpha ^ {m+} 1 ( E) $. | ||
A first-order uniformly elliptic system of general type in complex notation has the form | A first-order uniformly elliptic system of general type in complex notation has the form | ||
| − | + | $$ \tag{24 } | |
| + | \partial _ {\overline{z}\; } w - q _ {1} ( z) \partial _ {z} w - q _ {2} ( z) \partial _ {\overline{z}\; } \overline{w}\; + A w + B \overline{w}\; = 0 , | ||
| + | $$ | ||
| − | + | $$ | |
| + | | q _ {1} | + | q _ {2} | \leq q _ {0} = \textrm{ const } < 1 . | ||
| + | $$ | ||
It may be reduced to the form (7) with the aid of a homeomorphism defined by a solution of an equation of the type (20). | It may be reduced to the form (7) with the aid of a homeomorphism defined by a solution of an equation of the type (20). | ||
| − | Any solution of equation (24) in some bounded domain | + | Any solution of equation (24) in some bounded domain $ S $, |
| + | for the case $ A , B \in L _ {p} ( S) $, | ||
| + | $ p > 2 $, | ||
| + | can be represented in the form | ||
| − | + | $$ \tag{25 } | |
| + | w ( z) = \Phi [ \omega ( z) ] e ^ {\phi ( z) } , | ||
| + | $$ | ||
| − | where | + | where $ \omega ( z) $ |
| + | is some homeomorphism defined by a solution of the Beltrami equation (20) with the coefficient | ||
| − | + | $$ | |
| + | q ( z) = q _ {1} ( z) + q _ {2} ( z) | ||
| + | \frac{\partial _ {\overline{z}\; } \overline{w}\; | ||
| + | }{\partial _ {z} w } | ||
| + | , | ||
| + | $$ | ||
| − | + | $ \Phi ( \omega ) $ | |
| + | is an analytic function in the domain $ \omega ( S) $, | ||
| + | and the function $ \phi ( z) \in C _ \alpha ( E) $, | ||
| + | $ \alpha = ( p - 2 ) / p $, | ||
| + | is holomorphic outside $ S $ | ||
| + | and vanishes at infinity. The representation (25) is also valid if the coefficients of the left-hand side of equation (24) depend on $ w $ | ||
| + | and on its derivatives of any order, provided the above conditions hold for the solutions under study. Formula (25) is reversible, as is formula (15). | ||
Formula (25) permits one to transfer several properties of the classical theory of analytic functions to solutions of equation (24): the uniqueness theorem, the principle of the argument, the maximum principle, etc. | Formula (25) permits one to transfer several properties of the classical theory of analytic functions to solutions of equation (24): the uniqueness theorem, the principle of the argument, the maximum principle, etc. | ||
| − | A general quasi-conformal mapping | + | A general quasi-conformal mapping $ Q $ |
| + | is a solution of some uniformly elliptic system of the form (24) (if $ A \equiv B \equiv 0 $). | ||
| + | The converse proposition is also true. Accordingly, the above results permit one to solve the main problems in the theory of [[Quasi-conformal mapping|quasi-conformal mapping]] by a purely analytical method. | ||
| − | Systems of first-order equations of elliptic type with | + | Systems of first-order equations of elliptic type with $ 2n $, |
| + | $ n > 1 $, | ||
| + | unknown functions in two independent variables may, with certain natural restrictions, be reduced to the canonical form | ||
| − | + | $$ \tag{26 } | |
| + | \partial _ {\overline{z}\; } w - Q ( z) \partial _ {z} w + A w + B \overline{w}\; = 0 , | ||
| + | $$ | ||
| − | where | + | where $ w $ |
| + | is the unknown vector with $ n $ | ||
| + | complex-valued components, and $ Q $, | ||
| + | $ A $ | ||
| + | and $ B $ | ||
| + | are square matrices of order $ n $. | ||
| + | The theory of equations of the form (26) has many features in common with the case $ n = 1 $, | ||
| + | but has also its own special features. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.N. Vekua, "New methods for solving elliptic equations" , North-Holland (1967) (Translated from Russian) {{MR|0212370}} {{ZBL|0146.34301}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.N. Vekua, "Generalized analytic functions" , Pergamon (1962) (Translated from Russian) {{MR|0152665}} {{MR|0150320}} {{MR|0138774}} {{ZBL|0127.03505}} {{ZBL|0100.07603}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.N. Vekua, "Systems of first-order differential equations of elliptic type and boundary value problems, with an application to shell theory" ''Mat. Sb.'' , '''31''' : 2 (1952) pp. 217–314 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S. Bergman, "Integral operators in the theory of linear partial differential equations" , Springer (1961) {{MR|0141880}} {{ZBL|0093.28701}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> L. Bers, "Theory of pseudo-analytic functions" , New York Univ. Inst. Math. Mech. (1953) {{MR|0057347}} {{ZBL|0051.31603}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B.V. Boyarskii, "A general representation of solutions of an elliptic system of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031930/d031930292.png" /> equations in the plane" ''Dokl. Akad. Nauk. SSSR'' , '''122''' : 4 (1958) pp. 543–546 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B.V. Boyarskii, "Some boundary value problems for systems of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031930/d031930293.png" /> elliptic equations in the plane" ''Dokl. Akad. Nauk. SSSR'' , '''124''' : 1 (1959) pp. 15–18 (In Russian) {{MR|116140}} {{ZBL|}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> T. Carleman, "Sur les systèmes linéaires aux dérivées partielles du premier ordre à deux variables" ''C.R. Acad. Sci.'' , '''197''' (1933) pp. 471–474 {{MR|}} {{ZBL|0007.16202}} {{ZBL|59.0469.03}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A.V. Bitsadze, "Boundary value problems for second-order elliptic equations" , North-Holland (1968) (Translated from Russian) {{MR|0226183}} {{ZBL|0167.09401}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> Z.I. Khalilov, "On boundary value problems for an elliptic equation" ''Izv. Akad. Nauk. SSSR Ser. Mat.'' , '''11''' (1947) pp. 345–362 (In Russian) (French summary)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German) {{MR|0195654}} {{ZBL|}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.N. Vekua, "New methods for solving elliptic equations" , North-Holland (1967) (Translated from Russian) {{MR|0212370}} {{ZBL|0146.34301}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.N. Vekua, "Generalized analytic functions" , Pergamon (1962) (Translated from Russian) {{MR|0152665}} {{MR|0150320}} {{MR|0138774}} {{ZBL|0127.03505}} {{ZBL|0100.07603}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.N. Vekua, "Systems of first-order differential equations of elliptic type and boundary value problems, with an application to shell theory" ''Mat. Sb.'' , '''31''' : 2 (1952) pp. 217–314 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S. Bergman, "Integral operators in the theory of linear partial differential equations" , Springer (1961) {{MR|0141880}} {{ZBL|0093.28701}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> L. Bers, "Theory of pseudo-analytic functions" , New York Univ. Inst. Math. Mech. (1953) {{MR|0057347}} {{ZBL|0051.31603}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B.V. Boyarskii, "A general representation of solutions of an elliptic system of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031930/d031930292.png" /> equations in the plane" ''Dokl. Akad. Nauk. SSSR'' , '''122''' : 4 (1958) pp. 543–546 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B.V. Boyarskii, "Some boundary value problems for systems of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031930/d031930293.png" /> elliptic equations in the plane" ''Dokl. Akad. Nauk. SSSR'' , '''124''' : 1 (1959) pp. 15–18 (In Russian) {{MR|116140}} {{ZBL|}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> T. Carleman, "Sur les systèmes linéaires aux dérivées partielles du premier ordre à deux variables" ''C.R. Acad. Sci.'' , '''197''' (1933) pp. 471–474 {{MR|}} {{ZBL|0007.16202}} {{ZBL|59.0469.03}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A.V. Bitsadze, "Boundary value problems for second-order elliptic equations" , North-Holland (1968) (Translated from Russian) {{MR|0226183}} {{ZBL|0167.09401}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> Z.I. Khalilov, "On boundary value problems for an elliptic equation" ''Izv. Akad. Nauk. SSSR Ser. Mat.'' , '''11''' (1947) pp. 345–362 (In Russian) (French summary)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German) {{MR|0195654}} {{ZBL|}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Tutschke, "Partielle komplexe Differentialgleichungen in einer und mehreren komplexen Variablen" , Deutsch. Verlag Wissenschaft. (1977) {{MR|481388}} {{ZBL|0361.35002}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G.F. Carrier, C.E. Pearson, "Partial differential equations" , Acad. Press (1976) {{MR|0404823}} {{ZBL|0323.35001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> L. Bers, "An outline of the theory of pseudoanalytic functions" ''Bull. Amer. Math. Soc.'' , '''62''' (1956) pp. 291–331 {{MR|0081936}} {{ZBL|0072.07703}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Tutschke, "Partielle komplexe Differentialgleichungen in einer und mehreren komplexen Variablen" , Deutsch. Verlag Wissenschaft. (1977) {{MR|481388}} {{ZBL|0361.35002}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G.F. Carrier, C.E. Pearson, "Partial differential equations" , Acad. Press (1976) {{MR|0404823}} {{ZBL|0323.35001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> L. Bers, "An outline of the theory of pseudoanalytic functions" ''Bull. Amer. Math. Soc.'' , '''62''' (1956) pp. 291–331 {{MR|0081936}} {{ZBL|0072.07703}} </TD></TR></table> | ||
Revision as of 17:33, 5 June 2020
Methods for solving elliptic partial differential equations involving the representation of solutions by way of analytic functions of a complex variable.
The theory of analytic functions
$$ w ( z) = u ( x , y ) + i v ( x , y ) $$
of the complex variable $ z = x + iy $ is the theory of two real-valued functions $ u ( x , y ) $ and $ v ( x , y ) $ satisfying the Cauchy–Riemann system of equations $ u _ {x} - v _ {y} = 0 $, $ u _ {y} + v _ {x} = 0 $, which is essentially equivalent to the Laplace equation
$$ \Delta u \equiv u _ {xx} + u _ {yy} = 0 . $$
Since the 1930s, methods of analytic function theory have been used to an increasing extent in the general theory of equations of elliptic type. Thus arose a new branch of analysis, a substantial extension of the classical theory of analytic functions and their applications. The main subject of this branch are representation formulas for all solutions of a very extensive class of equations of elliptic type by analytic functions of one complex variable. For linear equations these representations are realized using certain linear operators, expressed in terms of the coefficients of the equations. These formulas make it possible to extend the properties of analytic functions to solutions of an equation of elliptic type, and important properties such as the uniqueness theorem, the principle of the argument, Liouville's theorem, etc., are often literally preserved. Taylor and Laurent series, the Cauchy integral formula, the compactness principle, the principle of analytic continuation, etc., are extended in a natural way.
The complex representation formulas permit the construction of various families of particular solutions of equations displaying certain properties. For instance, it is possible to construct various classes of so-called elementary solutions with point singularities, which are employed to obtain various integral formulas. So-called complete systems of particular solutions can be constructed; the latter have the property that their linear combinations approximate any solution. Complex representation formulas also make it possible to reduce many boundary value problems to equivalent problems for analytic functions, and to construct Fredholm or singular integral equations which are equivalent to these problems. Boundary value problems of non-Fredholm type may also be studied and a condition of normal solvability and explicit formulas for the index may thus be obtained. See Boundary value problem, complex-variable methods.
Elliptic equations with analytic coefficients.
Let the second-order equation of elliptic type
$$ \tag{1 } \Delta u + a ( x , y ) \frac{\partial u }{\partial x } + b ( x , y ) \frac{\partial u }{\partial y } + c ( x , y ) u = 0 $$
be given, where $ a $, $ b $ and $ c $ are analytic functions in the real variables $ x $ and $ y $ in some domain of the $ z $- plane, $ z = x + iy $. Analytic continuation of the coefficients into the domain of the independent complex variables $ z = x + iy $, $ \zeta = x - iy $ yields the following form of equation (1):
$$ \tag{2 } \frac{\partial ^ {2} u }{\partial z \partial \zeta } + A ( z , \zeta ) \frac{\partial u }{\partial z } + B ( z , \zeta ) \frac{\partial u }{\partial \zeta } + C ( z , \zeta ) u = 0 . $$
A simply-connected domain $ D _ {0} $ is said to be a fundamental domain for equation (1) if $ A $, $ B $ and $ C $ are analytic functions of two independent variables in the cylindrical domain $ ( D _ {0} , {\overline{D}\; } _ {0} ) $, where $ {\overline{D}\; } _ {0} $ denotes the mirror image of $ D _ {0} $ with respect to the real axis.
If $ D \subset D _ {0} $ is a simply-connected domain, all solutions of equation (1) regular in the domain $ D $ are expressed by the formula
$$ \tag{3 } u ( x , y ) = \mathop{\rm Re} \left \{ G ( z , z _ {0} ; z , z bar ) \Phi ( z) \right . - $$
$$ - \left . \int\limits _ {z _ {1} } ^ { z } \Phi ( t) \frac \partial { \partial t } G ( t , {\overline{z}\; } _ {0} , z , \overline{z}\; ) d t \right \} , $$
where $ \Phi ( z) $ is an arbitrary holomorphic function in $ D $, $ z _ {1} , z _ {0} \in D $ are arbitrary fixed points; the analytic function $ G ( z , \zeta ; y , \tau ) $ of four independent complex arguments in the cylindrical domain $ ( D _ {0} , {\overline{D}\; } _ {0} , D _ {0} , {\overline{D}\; } _ {0} ) $ is said to be the Riemann function of equation (1). It is the solution of the integral equation of Volterra type:
$$ \tag{4 } G ( z , \zeta ; t , \tau ) - \int\limits _ \tau ^ \zeta A ( z , \eta ,\ t , \tau ) d \eta + $$
$$ - \int\limits _ { t } ^ { z } B ( \xi , \zeta ) G ( \xi , \zeta ; t , \tau ) d \xi + $$
$$ + \int\limits _ { t } ^ { z } d \xi \int\limits _ \tau ^ \zeta C ( \xi , \eta ) G ( \xi , \eta ; t , \tau ) d \eta = 1 . $$
The correspondence between the family of solutions $ \{ u \} $ of equation (1) and the family of holomorphic functions $ \{ \Phi \} $ produced by formula (3) will be a one-to-one correspondence if the values of the imaginary parts of $ \Phi $ are fixed in a given point $ z _ {1} $ of $ D $. If $ z _ {1} = z _ {0} = 0 $, the inversion formula
$$ \Phi ( z) = 2 u \left ( \frac{z}{2} , \frac{z}{2i} \right ) - u ( 0 , 0 ) G ( 0 , 0 ; z , 0 ) $$
is valid. Equation (4) can be solved by the method of successive approximation. An approximate expression of the Riemann function can be obtained in this way.
If the domain $ D $ is multiply connected, formula (3) usually gives multi-valued solutions. In order to obtain all single-valued solutions of equation (1) in this case, multi-valued functions of a certain type must be taken for $ \Phi $ in (3).
Let $ D $ be a doubly-connected domain $ ( D \subset D _ {0} ) $; let $ D ^ \prime $ be a bounded continuum completing $ D $ to a simply-connected domain. All solutions of equation (1) which are single-valued in $ D $ are then given by the formula
$$ \tag{5 } u ( x , y ) = \mathop{\rm Re} \left \{ G ( z , {\overline{z}\; } _ {0} ; z ,\ \overline{z}\; ) \Phi ( z) \right . - $$
$$ - \left . \int\limits _ {z _ {1} } ^ { z } \Phi ( t) H ( t ,\ {\overline{z}\; } _ {0} , z , \overline{z}\; ) d t \right \} , $$
where $ z _ {1} \in D $, $ z _ {0} \in D ^ \prime $ are fixed points, and $ \Phi ( z) $ is a multi-valued analytic function of the form
$$ \Phi ( z) = \Phi _ {0} ( z) + \left [ \alpha G ( z _ {0} , {\overline{z}\; } _ {0} ; z , \overline{z}\; ) \right . - $$
$$ - \left . \frac{1}{2 \pi i } \int\limits _ { L } \overline{ {\Phi _ {0} ( t) }}\; H ^ {*} ( z _ {0} , t , z , {\overline{z}\; } _ {0} ) dt \right ] \mathop{\rm ln} ( z - z _ {0} ) . $$
Here, $ \alpha $ is an arbitrary real constant, $ \Phi _ {0} ( z) $ is an arbitrary holomorphic function in $ D $, and $ L $ is any simple, closed, piecewise-smooth curve lying in $ D $ and enclosing $ D ^ \prime $. The functions $ H $ and $ H ^ {*} $ are expressed by the formulas
$$ H ( t , \tau , z , \zeta ) = \frac \partial {\partial t } G ( t , \tau ; z , \zeta ) - B ( t , \tau ) G ( t , \tau ; z , \zeta ) , $$
$$ H ^ {*} ( t , \tau , z , \zeta ) = \frac \partial {\partial \tau } G ( t , \tau ; z , \zeta ) - A ( t , \tau ) G ( t , \tau ; z , \zeta ) . $$
Complex representations of the type (3) are also extended to a system of equations written in a vector form (1), where $ u $ is a vector with components $ u _ {1} \dots u _ {n} $, and $ a , b , c $ are square matrices of order $ n $ whose entries are analytic functions of the variables $ x , y $.
In a domain in which there is at least one positive solution $ u _ {0} > 0 $ for (1), equation (1) may be converted to the form
$$ \Delta v + a v _ {x} + b v _ {y} = 0 $$
by substituting $ u= u _ {0} v $. (Such a solution always exists in a small neighbourhood of any fixed point, and also in any domain where $ c \leq 0 $.) In this case equation (1) is equivalent to the system of equations
$$ \tag{6 } u _ {x} - v _ {y} + a u + b v = 0 ,\ \ u _ {y} + v _ {x} + c u + d v = 0 , $$
which is a special case of the generalized Cauchy–Riemann system. Introducing the complex function $ w = u + i v $, the system may be written as
$$ \tag{7 } \partial _ {\overline{z}\; } w + A ( z) w + B ( z) \overline{w}\; = 0 ,\ \ 2 \partial _ {\overline{z}\; } = \partial _ {x} + i \partial _ {y} . $$
If the coefficients $ A $ and $ B $ are analytic functions of the complex arguments $ z $ and $ \zeta $( $ z = x + i y $, $ \zeta = x - i y $) in some cylindrical domain $ ( D _ {0} , {\overline{D}\; } _ {0} ) $, where $ D _ {0} $ is a simply-connected domain, then the solution of equation (7) in a simply-connected domain $ D \subset D _ {0} $ is given by the formula:
$$ \tag{8 } w ( z) = \mathop{\rm exp} \left \{ \int\limits _ {z _ {0} } ^ { z } A ( z ,\ \tau ) d \tau \right \} \times $$
$$ \times \left \{ \Phi ( z) + \int\limits _ {z _ {0} } ^ { z } {\widetilde \Gamma } _ {1} ( z , \overline{z}\; , t ) \Phi ( t) d t + \int\limits _ { {\overline{z}\; } _ {0} } ^ { {z } bar } {\widetilde \Gamma } _ {2} ( z , \overline{z}\; , t ) \Phi ( t) d t \right \} , $$
where $ {\widetilde \Gamma } _ {1} $ and $ {\widetilde \Gamma } _ {2} $ are analytic functions of their arguments, defined in terms of $ A $ and $ B $ and constructed by the method of successive approximation; $ \Phi $ is an arbitrary analytic function of the variable $ z $.
If $ A $ and $ B $ are entire functions of the variables $ x $ and $ y $, the representation (8) is valid for any simply-connected domain of the $ z $- plane, irrespective of the behaviour of the coefficients $ A $ and $ B $ near infinity.
Let the elliptic equation
$$ \tag{9 } \Delta ^ {n} u + \sum _ {k = 1 } ^ { n } \sum _ {0 \leq p + q \leq k } a _ {p , q } ^ {( k) } \frac{\partial ^ {p+} q \Delta ^ {n-} k u }{\partial x ^ {p} \partial y ^ {q} } = 0 $$
be given, where $ a _ {p,q} ^ {( k) } $ are analytic functions of $ x $ and $ y $. If $ D _ {0} $ is a fundamental domain for equation (9), any regular solution of this equation in a simply-connected domain $ D \subset D _ {0} $ is expressed by the formula
$$ \tag{10 } u ( x , y ) = \mathop{\rm Re} \left \{ G ( z , z _ {0} ; z , z bar ) \Phi _ {0} ( z) \right . - $$
$$ - \left . \sum _ {k = 0 } ^ { n- } 1 \int\limits _ {z _ {1} } ^ { z } \Phi _ {k} ( t) \frac \partial {\partial t } G _ {k} ( t , {z bar } _ {0} ; z , \overline{z}\; ) d t \right \} , $$
where $ \Phi _ {0} \dots \Phi _ {n-} 1 $ are arbitrary functions holomorphic in $ D $, and
$$ G _ {k} ( t , \tau ; z , \zeta ) = \frac{\partial ^ {2 ( n - k - 1 ) } G ( t , \tau ; z , \zeta ) }{\partial t ^ {n-} k- 1 \partial \tau ^ {n-} k- 1 } ,\ k = 0 \dots n - 1 . $$
Here $ G $ is the complex Riemann function of equation (9) which depends analytically on the complex arguments $ ( t , \tau , z , \zeta ) $ in the cylindrical domain $ ( D _ {0} , {\overline{D}\; } _ {0} , D _ {0} , {\overline{D}\; } _ {0} ) $. If the conditions
$$ \Phi _ {k} ( z _ {1} ) = \overline{ {\Phi _ {k} ( z _ {1} ) }}\; , \ k = 0 \dots n - 1 , $$
are satisfied, formula (10) realizes a one-to-one correspondence between the family of solutions $ \{ u \} $ of equation (9) and the family of holomorphic functions $ \{ ( \Phi _ {0} \dots \Phi _ {n-} 1 ) \} $. If $ D $ is a multiply-connected domain, formula (10) usually yields multi-valued solutions. However, as for equations of the second order, the formula may be modified so that it yields all single-valued solutions of equation (9) in a multiply-connected domain as well. Formula (10) may also be extended to a system of equations such as (9), where $ u $ is a vector and the coefficients are matrices.
For several equations of mathematical physics the Riemann function is explicitly given using elementary or special functions.
For the equation of the vibrating membrane,
$$ \Delta u + \lambda ^ {2} u = 0 ,\ \lambda = \textrm{ const } , $$
$$ G ( z , \zeta ; t , \tau ) = J _ {0} ( \lambda \sqrt {( z - t ) ( \zeta - \tau ) } ) , $$
where $ J _ {0} $ is the Bessel function of order zero, and the complex plane is taken as fundamental domain. The case $ \lambda = 0 $ yields the Laplace equation $ \Delta u = 0 $; then $ G = 1 $ and formula (3) assumes the form
$$ u = \mathop{\rm Re} [ \Phi ( z) ] . $$
For the equation of spherical functions,
$$ \Delta u + n ( n + 1 ) ( 1 + x ^ {2} + y ^ {2} ) ^ {-} 2 u = \ 0 ,\ n = \textrm{ const } , $$
$$ G ( z , \zeta ; t , \tau ) = P _ {n} \left ( \frac{( 1 - z \zeta ) ( 1 - t \tau ) + 2 z \tau + 2 \zeta t }{( 1 + z \zeta ) ( 1 + t \tau ) } \right ) , $$
where $ P _ {n} $ is the Legendre function of the first kind; any simply-connected domain $ D _ {0} $ which satisfies the condition: if $ z \in D _ {0} $, $ \zeta \in D _ {0} $, then $ z \zeta \neq 1 $( e.g. the disc $ | z | < 1 $), may be taken as fundamental domain. In the case of the Euler–Darboux equation
$$ \Delta u + y ^ {-} 1 ( \alpha u _ {x} + \alpha ^ \prime u _ {y} ) = \ 0 ,\ \alpha , \alpha ^ \prime = \textrm{ const } , $$
$$ G ( z , \zeta ; t , \tau ) = ( \tau - z ) ^ {- \beta ^ \prime } ( \zeta - t ) ^ {- \beta } ( \zeta - z ) ^ {\beta + \beta ^ \prime } \times $$
$$ \times F \left ( \beta ^ \prime , \beta , 1 , \frac{( z - t ) ( \zeta - \tau ) }{( z - t ) ( \zeta - t ) } \right ) , $$
where $ 2 \beta = \alpha ^ \prime + i \alpha $, $ 2 \beta ^ \prime = \alpha ^ \prime - i \alpha $, and $ F $ is the hypergeometric series; the half-planes $ y > 0 $ or $ y < 0 $ may be taken as fundamental domains.
For the equation
$$ \Delta ^ {n} u = 0 ,\ n = 1 , 2 \dots $$
$$ G ( z , \zeta ; t , \tau ) = \frac{( z - 1 ) ^ {n-} 1 ( \zeta - t ) ^ {n-} 1 }{( n - 1 ) ! ( n - 1 ) ! } , $$
Goursat's formula
$$ u = \mathop{\rm Re} [ ( z \overline{z}\; ) ^ {n-} 1 \Phi _ {n-} 1 + ( z \overline{z}\; ) ^ {n-} 2 \Phi _ {n-} 2 + \dots + \Phi _ {0} ] $$
is valid.
The method of complex representation of solutions is also applicable to a certain class of non-linear equations. For instance, let the Gauss equation
$$ \Delta u = - 2 k e ^ {u} $$
be given, where $ k ( x , y ) $ is a given function (this is a well-known equation in differential geometry). If $ v _ {0} ( z) $ is any particular solution of this equation, the functions of the type
$$ u ( z) = v _ {0} [ \Phi ( z) ] | \Phi ^ \prime ( z) | ^ {2} , $$
where $ \Phi ( z) $ is an arbitrary analytic function, are also solutions. If $ k = \textrm{ const } $, then $ v _ {0} = 4 ( 1 - k z \overline{z}\; ) ^ {-} 2 $ and all solutions of the Gauss equation may be expressed by the formula:
$$ u ( x , y ) = 4 | \Phi ^ \prime ( z) | ^ {2} ( 1 + k | \Phi ( z) | ^ {2} ) ^ {-} 2 . $$
If $ k < 0 $, it should be assumed that $ | \Phi ( z) | < - k ^ {-} 1 $.
Elliptic equations with non-analytic coefficients.
Let there be given a generalized system of Cauchy–Riemann equations (7) with coefficients $ A $ and $ B $ defined on the whole complex $ z $- plane $ E $ and belonging to the class $ L _ {p,2} ( E) $, i.e.
$$ A ( z) , B ( z) \in L _ {p} ,\ | z | ^ {-} 2 A \left ( \frac{1}{z} \right ) , | z | ^ {-} 2 B \left ( \frac{1}{z} \right ) \in \ L _ {p} , $$
$$ p > 2 ,\ | z | \leq 1 . $$
If the coefficients are given in a bounded domain $ S $ and belong to the class $ L _ {p} ( S) $, $ p > 2 $, they will satisfy the above conditions when extended by zero outside $ S $. Under these assumptions, equation (7) usually has no solutions in the classical sense. One accordingly considers a so-called generalized solution: A function $ w ( z) \in L _ {1} ( S) $ is called a solution of equation (7) in $ S $ if it has a derivative in the generalized sense (as defined by S.L. Sobolev) $ \partial _ {\overline{z}\; } w \in L _ {1} ( S) $ and satisfies the equation almost-everywhere in $ S $.
The theory of functions satisfying equation (7) is a far-reaching generalization of the classical theory of analytic functions $ ( A \equiv B \equiv 0 ) $ and retains their principal features. For this reason solutions of equations of the type (7) are known as generalized analytic functions (cf. Generalized analytic function).
Any solution of equation (7) (in $ S $) satisfies the integral equation
$$ \tag{11 } w ( z) - \frac{1} \pi {\int\limits \int\limits } _ { S } \frac{A ( \zeta ) w ( \zeta ) + B ( \zeta ) \overline{ {w ( \zeta ) }}\; }{\zeta - z } d \xi d \eta = \Phi ( z) , $$
where $ \zeta = \xi + i \eta $ and $ \Phi ( z) $ is a holomorphic function in $ S $. If $ \Phi \in L _ {q} ( \overline{S}\; ) $, $ q \geq p / ( p - 1 ) $, $ p > 2 $, equation (11) has a unique solution, which is expressed by the formula
$$ \tag{12 } w ( z) = \Phi ( z) + {\int\limits \int\limits } _ { S } \Gamma _ {1} ( z , \zeta ) \Phi ( \zeta ) d \xi d \eta + $$
$$ + {\int\limits \int\limits } _ { S } \Gamma _ {2} ( z , \zeta ) \overline{ {\Phi ( \zeta ) }}\; d \xi d \eta . $$
The resolvents $ \Gamma _ {1} $ and $ \Gamma _ {2} $ depend on the coefficients of equation (7) and are constructed by the method of successive approximation.
Formula (12) gives a general (linear) representation of solutions of (7) by analytic functions $ \Phi ( z) $. In particular, it permits the construction of the so-called fundamental kernels
$$ \Omega _ {1} ( z , t ) = X _ {1} ( z , t ) + i X _ {2} ( z , t) , $$
$$ \Omega _ {2} ( z , t ) = X _ {1} ( z , t ) - i X _ {2} ( z , t ), $$
where $ t $ is some fixed point, and $ X _ {1} $ and $ X _ {2} $ are solutions of the integral equation (11) corresponding to the functions
$$ 2 \Phi _ {1} = ( t - z ) ^ {-} 1 ,\ 2 i \Phi _ {2} = ( t - z ) ^ {-} 1 . $$
These kernels permit one to state the generalized Cauchy formula:
$$ \tag{13 } \frac{1}{2 \pi i } \int\limits _ {\partial S } \Omega _ {1} ( z , \zeta ) w ( \zeta ) d \zeta - \Omega _ {2} ( z , \zeta ) \overline{ {w ( \zeta ) }}\; d \zeta bar = $$
$$ = \ \left \{ \begin{array}{ll} w ( z) , & z \in S , \\ w( \frac{z)}{2} , & z \in \partial S , \\ 0 , & z \notin \overline{S}\; . \\ \end{array} \right .$$
If $ A \equiv B \equiv 0 $, this formula becomes the classical Cauchy formula. Formula (13) may serve to extend many properties of analytic functions which are usually demonstrated by the Cauchy formula to generalized analytic functions. In particular, it is possible to generalize the classical theorems on analytic continuation, to construct a theory of generalized integrals of Cauchy type to obtain representations of generalized analytic functions in the form of contour integrals with a real density, etc.
The functions
$$ \Omega _ {1} ^ {*} ( z , t ) = - \Omega _ {1} ( t , z ) ,\ \ \Omega _ {2} ^ {*} ( z , t ) = - \overline{ {\Omega _ {2} ( t , z ) }}\; $$
are the fundamental kernels of the adjoint equation
$$ \tag{14 } \partial _ {\overline{z}\; } w _ {*} - A w _ {*} - \overline{ {B w _ {*} }}\; = 0 . $$
If, in $ S $, $ w $ and $ w _ {*} $ satisfy the equations (7) and (14), respectively, and if they are continuous in $ \overline{S}\; $, one has the identity (the analogue of the classical Cauchy theorem):
$$ \mathop{\rm Re} \left [ i \int\limits _ {\partial S } w ( z) w _ {*} ( z) d z \right ] = 0 . $$
If $ w ( z) $ is a solution of equation (7) in the domain $ S $, there exists an analytic function $ \Phi ( z) $ in $ S $ such that
$$ \tag{15 } w ( z) = \Phi ( z) e ^ {\omega ( z) } , $$
where
$$ \tag{16 } \omega ( z) = \frac{1} \pi {\int\limits \int\limits } _ { S } \frac{A ( \zeta ) + B ( \zeta ) ( w bar ( \zeta ) / w ( \zeta )) }{\zeta - z } d \xi d \eta , $$
and which belongs to the class $ C _ \alpha ( E) $, $ \alpha = p / ( p - 2 ) $; moreover, $ \omega ( z) \rightarrow 0 $ as $ z \rightarrow \infty $.
In particular, this formula permits the extension of fundamental theorems of the classical theory of analytic functions — the uniqueness theorem, Liouville's theorem, the principle of the argument, the compactness principle, etc. — to the solutions of equations such as (7). Formula (16) may be reversed: Given an analytic function $ \Phi $ it is possible to find a function $ w ( z) $ satisfying the non-linear integral equation (16).
Let $ \Phi ( z) $ be an analytic function in a domain $ S $, which may have arbitrary singularities, and let $ t $ be a fixed point. Then there exists a solution $ w ( z) $ of equation (7) such that the function $ w _ {0} = w / \Phi $ is continuously extendable onto the whole plane $ E $, belongs to the class $ C _ \alpha ( E) $, $ \alpha = ( p - 2 ) / p $, does not vanish anywhere in $ E $, and $ w _ {0} ( t)= 1 $. The function $ w _ {0} $ satisfies the integral equation
$$ \tag{17 } w _ {0} ( z) - \frac{z - t } \pi {\int\limits \int\limits } _ { S } \frac{A ( \zeta ) w _ {0} ( \zeta ) + B _ {0} ( \zeta ) {w _ {0} ( \zeta ) } bar }{( \zeta - z ) ( \zeta - t ) } d \xi d \eta = 1 , $$
$$ B _ {0} = B \frac{\overline \Phi \; } \Phi , $$
which has a unique solution, while the function $ w = \Phi ( z) w _ {0} $ satisfies the non-linear integral equation
$$ \tag{18 } w ( z) = $$
$$ = \ \Phi ( z) \mathop{\rm exp} \left \{ \frac{z - t } \pi {\int\limits \int\limits } _ { S } \frac{A ( \zeta ) w ( \zeta ) + B ( \zeta ) \overline{ {w ( \zeta ) }}\; }{ ( \zeta - z ) ( \zeta - t ) w } d \xi d \eta \right \} , $$
from which, as $ t \rightarrow \infty $, the representation (15) is obtained.
The problem of reducing a second-order elliptic equation of general type
$$ \tag{19 } a \frac{\partial ^ {2} u }{\partial x ^ {2} } + 2 b \frac{\partial ^ {2} u }{\partial x \partial y } + c \frac{\partial ^ {2} u }{\partial y ^ {2} } + d \frac{ \partial u }{\partial x } + e \frac{\partial u }{\partial y } + f ( u) = 0 $$
to the form (1) is equivalent to the problem of reducing the positive quadratic form
$$ a d x ^ {2} + 2 b d x d y + c d y ^ {2} ,\ a > 0 ,\ \Delta \equiv a c - b ^ {2} > 0 , $$
to canonical form. This problem is equivalent to finding the homeomorphisms defined by the solution of the Beltrami equation
$$ \tag{20 } \partial _ {\overline{z}\; } w - q ( z) \partial _ {z} w = 0 ,\ \ w = \widetilde{x} + i \widetilde{y} , $$
where
$$ q ( z) = ( a - \sqrt \Delta - i b ) ( a + \sqrt \Delta + i b ) ^ {-} 1 ,\ | q ( z) | < 1 . $$
If (19) is a uniformly elliptic equation ( $ \Delta \geq \Delta _ {0} = \textrm{ const } > 0 $), then $ | q ( z) | \leq q _ {0} = \textrm{ const } < 1 $.
The principal problem in the study of the Beltrami equation is the construction of a solution in a given domain $ S $; if $ \omega ( z) $ is a solution of the Beltrami equation realizing a homeomorphism of the domain $ S $ onto the domain $ \omega ( S) $, then any other solution of the equation in $ S $ has the form
$$ \tag{21 } w ( z) = \Phi [ \omega ( z) ] , $$
where $ \Phi $ is an arbitrary analytic function in $ \omega ( S) $.
If $ q ( z) $ is measurable, $ q ( z) \equiv 0 $ outside $ S $ and $ | q ( z) | \leq q _ {0} < 1 $, the Beltrami equation has a solution of the form
$$ \tag{22 } w ( z) = z - \frac{1} \pi {\int\limits \int\limits } _ { E } \frac{\rho ( \zeta ) d \xi d \eta }{\zeta - z } , $$
where $ \rho $ satisfies the singular integral equation
$$ \tag{23 } \rho ( z) - \frac{q ( z) } \pi {\int\limits \int\limits } _ { E } \frac{\rho ( \zeta ) d \xi d \eta }{( \zeta - z ) ^ {2} } = q ( z) , $$
in which the integral is understood in the sense of the Cauchy principal value. This equation has a unique solution in some class $ L _ {p} ( E) $, $ p > 2 $, and may be obtained by the method of successive approximation. The function (22) belongs to the class $ C _ \alpha ( E) $, $ \alpha = p / ( p - 2 ) $, realizes a homeomorphism of the plane onto itself, and $ w ( \infty ) = \infty $, $ z ^ {-} 1 w ( z) \rightarrow 1 $ as $ z \rightarrow \infty $. If $ q \in C _ \alpha ^ {m} ( E) $, $ 0 < \alpha < 1 $, $ m \geq 0 $, then $ w ( z) \in C _ \alpha ^ {m+} 1 ( E) $.
A first-order uniformly elliptic system of general type in complex notation has the form
$$ \tag{24 } \partial _ {\overline{z}\; } w - q _ {1} ( z) \partial _ {z} w - q _ {2} ( z) \partial _ {\overline{z}\; } \overline{w}\; + A w + B \overline{w}\; = 0 , $$
$$ | q _ {1} | + | q _ {2} | \leq q _ {0} = \textrm{ const } < 1 . $$
It may be reduced to the form (7) with the aid of a homeomorphism defined by a solution of an equation of the type (20).
Any solution of equation (24) in some bounded domain $ S $, for the case $ A , B \in L _ {p} ( S) $, $ p > 2 $, can be represented in the form
$$ \tag{25 } w ( z) = \Phi [ \omega ( z) ] e ^ {\phi ( z) } , $$
where $ \omega ( z) $ is some homeomorphism defined by a solution of the Beltrami equation (20) with the coefficient
$$ q ( z) = q _ {1} ( z) + q _ {2} ( z) \frac{\partial _ {\overline{z}\; } \overline{w}\; }{\partial _ {z} w } , $$
$ \Phi ( \omega ) $ is an analytic function in the domain $ \omega ( S) $, and the function $ \phi ( z) \in C _ \alpha ( E) $, $ \alpha = ( p - 2 ) / p $, is holomorphic outside $ S $ and vanishes at infinity. The representation (25) is also valid if the coefficients of the left-hand side of equation (24) depend on $ w $ and on its derivatives of any order, provided the above conditions hold for the solutions under study. Formula (25) is reversible, as is formula (15).
Formula (25) permits one to transfer several properties of the classical theory of analytic functions to solutions of equation (24): the uniqueness theorem, the principle of the argument, the maximum principle, etc.
A general quasi-conformal mapping $ Q $ is a solution of some uniformly elliptic system of the form (24) (if $ A \equiv B \equiv 0 $). The converse proposition is also true. Accordingly, the above results permit one to solve the main problems in the theory of quasi-conformal mapping by a purely analytical method.
Systems of first-order equations of elliptic type with $ 2n $, $ n > 1 $, unknown functions in two independent variables may, with certain natural restrictions, be reduced to the canonical form
$$ \tag{26 } \partial _ {\overline{z}\; } w - Q ( z) \partial _ {z} w + A w + B \overline{w}\; = 0 , $$
where $ w $ is the unknown vector with $ n $ complex-valued components, and $ Q $, $ A $ and $ B $ are square matrices of order $ n $. The theory of equations of the form (26) has many features in common with the case $ n = 1 $, but has also its own special features.
References
| [1] | I.N. Vekua, "New methods for solving elliptic equations" , North-Holland (1967) (Translated from Russian) MR0212370 Zbl 0146.34301 |
| [2] | I.N. Vekua, "Generalized analytic functions" , Pergamon (1962) (Translated from Russian) MR0152665 MR0150320 MR0138774 Zbl 0127.03505 Zbl 0100.07603 |
| [3] | I.N. Vekua, "Systems of first-order differential equations of elliptic type and boundary value problems, with an application to shell theory" Mat. Sb. , 31 : 2 (1952) pp. 217–314 (In Russian) |
| [4] | S. Bergman, "Integral operators in the theory of linear partial differential equations" , Springer (1961) MR0141880 Zbl 0093.28701 |
| [5] | L. Bers, "Theory of pseudo-analytic functions" , New York Univ. Inst. Math. Mech. (1953) MR0057347 Zbl 0051.31603 |
| [6] | B.V. Boyarskii, "A general representation of solutions of an elliptic system of 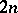 equations in the plane" Dokl. Akad. Nauk. SSSR , 122 : 4 (1958) pp. 543–546 (In Russian) equations in the plane" Dokl. Akad. Nauk. SSSR , 122 : 4 (1958) pp. 543–546 (In Russian) |
| [7] | B.V. Boyarskii, "Some boundary value problems for systems of 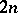 elliptic equations in the plane" Dokl. Akad. Nauk. SSSR , 124 : 1 (1959) pp. 15–18 (In Russian) MR116140 elliptic equations in the plane" Dokl. Akad. Nauk. SSSR , 124 : 1 (1959) pp. 15–18 (In Russian) MR116140 |
| [8] | T. Carleman, "Sur les systèmes linéaires aux dérivées partielles du premier ordre à deux variables" C.R. Acad. Sci. , 197 (1933) pp. 471–474 Zbl 0007.16202 Zbl 59.0469.03 |
| [9] | A.V. Bitsadze, "Boundary value problems for second-order elliptic equations" , North-Holland (1968) (Translated from Russian) MR0226183 Zbl 0167.09401 |
| [10] | Z.I. Khalilov, "On boundary value problems for an elliptic equation" Izv. Akad. Nauk. SSSR Ser. Mat. , 11 (1947) pp. 345–362 (In Russian) (French summary) |
| [11] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) MR0195654 |
Comments
References
| [a1] | W. Tutschke, "Partielle komplexe Differentialgleichungen in einer und mehreren komplexen Variablen" , Deutsch. Verlag Wissenschaft. (1977) MR481388 Zbl 0361.35002 |
| [a2] | G.F. Carrier, C.E. Pearson, "Partial differential equations" , Acad. Press (1976) MR0404823 Zbl 0323.35001 |
| [a3] | L. Bers, "An outline of the theory of pseudoanalytic functions" Bull. Amer. Math. Soc. , 62 (1956) pp. 291–331 MR0081936 Zbl 0072.07703 |
Differential equation, partial, complex-variable methods. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_equation,_partial,_complex-variable_methods&oldid=24413