Differential calculus (on analytic spaces)
A generalization of the classical calculus of differential forms and differential operators to analytic spaces. For the calculus of differential forms on complex manifolds see Differential form. Let 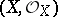 be an analytic space over a field
be an analytic space over a field 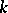 , let
, let 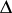 be the diagonal in
be the diagonal in 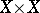 , let
, let 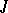 be the sheaf of ideals defining
be the sheaf of ideals defining 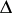 and generated by all germs of the form
and generated by all germs of the form 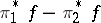 , where
, where 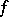 is an arbitrary germ from
is an arbitrary germ from 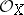 , and let
, and let 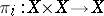 be projection on the
be projection on the  -th factor.
-th factor.
The analytic sheaf 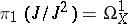 is known as the sheaf of analytic differential forms of the first order on
is known as the sheaf of analytic differential forms of the first order on 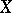 . If
. If 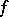 is the germ of an analytic function on
is the germ of an analytic function on 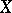 , then the germ
, then the germ 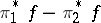 belongs to
belongs to 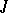 and defines the element
and defines the element 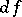 of
of 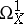 known as the differential of the germ
known as the differential of the germ 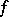 . This defines a sheaf homomorphism of vector spaces
. This defines a sheaf homomorphism of vector spaces 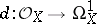 . If
. If 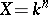 , then
, then 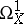 is the free sheaf generated by
is the free sheaf generated by 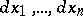 , where
, where  are the coordinates in
are the coordinates in 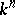 . If
. If 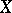 is an analytic subspace in
is an analytic subspace in 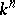 , defined by a sheaf of ideals
, defined by a sheaf of ideals 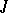 , then
, then
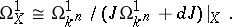 |
Each analytic mapping 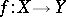 may be related to a sheaf of relative differentials
may be related to a sheaf of relative differentials 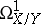 . This is the analytic sheaf
. This is the analytic sheaf 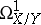 inducing
inducing 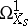 on each fibre
on each fibre 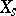 (
(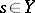 ) of
) of 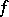 ; it is defined from the exact sequence
; it is defined from the exact sequence
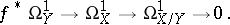 |
The sheaf 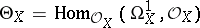 is called the sheaf of germs of analytic vector fields on
is called the sheaf of germs of analytic vector fields on  . If
. If  is a manifold,
is a manifold,  and
and 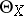 are locally free sheaves, which are naturally isomorphic to the sheaf of analytic sections of the cotangent and the tangent bundle over
are locally free sheaves, which are naturally isomorphic to the sheaf of analytic sections of the cotangent and the tangent bundle over 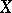 , respectively.
, respectively.
The analytic sheaves 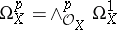 are called sheaves of analytic exterior differential forms of degree
are called sheaves of analytic exterior differential forms of degree 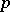 on
on 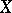 (if
(if 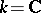 , they are also called holomorphic forms). For any
, they are also called holomorphic forms). For any 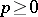 one may define a sheaf homomorphism of vector spaces
one may define a sheaf homomorphism of vector spaces 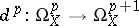 , which for
, which for 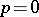 coincides with the one introduced above, and which satisfies the condition
coincides with the one introduced above, and which satisfies the condition 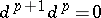 . The complex of sheaves
. The complex of sheaves 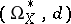 is called the de Rham complex of the space
is called the de Rham complex of the space 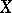 . If
. If 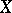 is a manifold and
is a manifold and 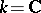 or
or 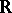 , the de Rham complex is an exact complex of sheaves. If
, the de Rham complex is an exact complex of sheaves. If 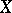 is a Stein manifold or a real-analytic manifold, the cohomology groups of the complex of sections
is a Stein manifold or a real-analytic manifold, the cohomology groups of the complex of sections 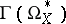 , which is also often referred to as the de Rham complex, are isomorphic to
, which is also often referred to as the de Rham complex, are isomorphic to 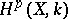 .
.
If 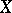 has singular points, the de Rham complex need not be exact. If
has singular points, the de Rham complex need not be exact. If 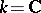 , a sufficient condition for the exactness of the de Rham complex at a point
, a sufficient condition for the exactness of the de Rham complex at a point 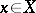 is the presence of a complex-analytic contractible neighbourhood at
is the presence of a complex-analytic contractible neighbourhood at  . The hyperhomology groups of the complex
. The hyperhomology groups of the complex 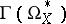 contain, for
contain, for 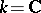 , the cohomology groups of the space
, the cohomology groups of the space 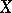 with coefficients in
with coefficients in 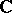 as direct summands, and are identical with them if
as direct summands, and are identical with them if 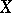 is smooth. The sections of the sheaf
is smooth. The sections of the sheaf 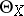 are called analytic (and if
are called analytic (and if 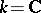 , also holomorphic) vector fields on
, also holomorphic) vector fields on 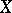 . For any open
. For any open 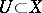 the field
the field 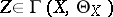 defines a derivation in the algebra of analytic functions
defines a derivation in the algebra of analytic functions 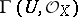 , acting according to the formula
, acting according to the formula 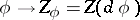 . If
. If 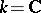 or
or 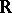 , then
, then 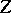 defines a local one-parameter group
defines a local one-parameter group 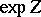 of automorphisms of the space
of automorphisms of the space 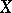 . If, in addition,
. If, in addition, 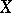 is compact, the group
is compact, the group 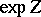 is globally definable.
is globally definable.
The space 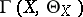 provided with the Lie bracket is a Lie algebra over
provided with the Lie bracket is a Lie algebra over 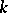 . If
. If 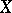 is a compact complex space,
is a compact complex space, 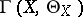 is the Lie algebra of the group
is the Lie algebra of the group 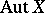 .
.
Differential operators on an analytic space 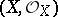 are defined in analogy to the differential operators on a module (cf. Differential operator on a module). If
are defined in analogy to the differential operators on a module (cf. Differential operator on a module). If 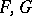 are analytic sheaves on
are analytic sheaves on 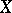 , then a linear differential operator of order
, then a linear differential operator of order 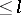 , acting from
, acting from 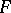 into
into 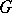 , is a sheaf homomorphism of vector spaces
, is a sheaf homomorphism of vector spaces 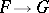 which extends to an analytic homomorphism
which extends to an analytic homomorphism 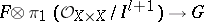 . If
. If 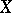 is smooth and
is smooth and 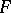 and
and 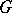 are locally free, this definition gives the usual concept of a differential operator on a vector bundle , [4].
are locally free, this definition gives the usual concept of a differential operator on a vector bundle , [4].
The germs of the linear differential operators 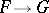 form an analytic sheaf
form an analytic sheaf 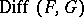 with filtration
with filtration
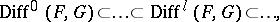 |
where 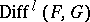 is the sheaf of germs of operators of order
is the sheaf of germs of operators of order 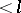 . In particular,
. In particular, 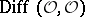 is a filtered sheaf of associative algebras over
is a filtered sheaf of associative algebras over 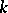 under composition of mappings. One has
under composition of mappings. One has
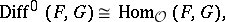 |
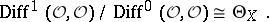 |
The sheaf 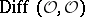 was studied (for the non-smooth case) only for certain special types of singular points. In particular, it was proved in the case of an irreducible one-dimensional complex space
was studied (for the non-smooth case) only for certain special types of singular points. In particular, it was proved in the case of an irreducible one-dimensional complex space 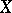 that the sheaf of algebras
that the sheaf of algebras 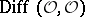 and the corresponding sheaf of graded algebras have finite systems of generators [5].
and the corresponding sheaf of graded algebras have finite systems of generators [5].
References
| [1] | B. Malgrange, "Analytic spaces" Enseign. Math. Ser. 2 , 14 : 1 (1968) pp. 1–28 |
| [2] | W. Kaup, "Infinitesimal Transformationsgruppen komplexer Räume" Math. Ann. , 160 : 1 (1965) pp. 72–92 |
| [3a] | L. Schwartz, "Variedades analiticas complejas elipticas" , Univ. Nac. Colombia (1956) |
| [3b] | L. Schwartz, "Ecuaciones differenciales parciales" , Univ. Nac. Colombia (1956) |
| [4] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
| [5] | Th. Bloom, "Differential operators on curves" Rice Univ. Stud. , 59 : 2 (1973) pp. 13–19 |
| [6] | R. Berger, R. Kiehl, E. Kunz, H.-J. Nastold, "Differentialrechnung in der analytischen Geometrie" , Springer (1967) |
| [7] | G. Fischer, "Complex analytic geometry" , Springer (1976) |
Differential calculus (on analytic spaces). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_calculus_(on_analytic_spaces)&oldid=14009