Differential algebra
A branch of algebra which deals with objects which involve not only addition and multiplication operations but also the operation of differentiation: differential rings, differential modules, differential fields, and differential algebraic varieties.
One of the main objects of differential algebra is the algebra of differential polynomials 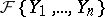 , which is the analogue of the ring of polynomials in commutative algebra (cf. Extension of a differential field). Each system of differential equations
, which is the analogue of the ring of polynomials in commutative algebra (cf. Extension of a differential field). Each system of differential equations
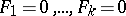 |
corresponds to the perfect differential ideal 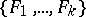 generated by this system in the algebra of differential polynomials. The Ritt–Raudenbush basis theorem states that all perfect differential ideals are obtained in this way (a differential ideal
generated by this system in the algebra of differential polynomials. The Ritt–Raudenbush basis theorem states that all perfect differential ideals are obtained in this way (a differential ideal 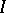 is called perfect if whenever
is called perfect if whenever 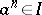 for some
for some 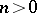 , then
, then 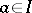 ), i.e. it is possible to select in any such ideal a finite number of differential polynomials such that the perfect differential ideal generated by these polynomials corresponds to the given ideal. As distinct from Hilbert's basis theorem in a polynomial ring, the essential feature of the Ritt–Raudenbush theorem is that the ideals are perfect, i.e. differential ideals (even perfect differential ideals) need not be finitely-generated differential modules.
), i.e. it is possible to select in any such ideal a finite number of differential polynomials such that the perfect differential ideal generated by these polynomials corresponds to the given ideal. As distinct from Hilbert's basis theorem in a polynomial ring, the essential feature of the Ritt–Raudenbush theorem is that the ideals are perfect, i.e. differential ideals (even perfect differential ideals) need not be finitely-generated differential modules.
A perfect differential ideal corresponds to a differential algebraic variety — the set of points in an affine space over some universal extension of the field of coefficients on which any polynomial from this ideal vanishes. The analogue of Hilbert's Nullstellensatz is valid. Let 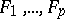 be a finite system of differential polynomials and let
be a finite system of differential polynomials and let 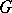 be a differential polynomial which vanishes in all solutions of this system. A certain power of
be a differential polynomial which vanishes in all solutions of this system. A certain power of 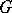 will then be a linear combination of the
will then be a linear combination of the 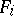 and their derivatives of various orders with coefficients from the algebra of differential polynomials. In particular, if the system
and their derivatives of various orders with coefficients from the algebra of differential polynomials. In particular, if the system 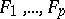 has no zeros, then some linear combination of the
has no zeros, then some linear combination of the 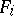 and their derivatives of various orders will be equal to one.
and their derivatives of various orders will be equal to one.
A perfect differential ideal may be represented as the intersection of a finite number of prime differential ideals. To such a representation corresponds the decomposition of a variety into a finite number of irreducible components. As in algebraic geometry, the concept of a generic zero and its dimension is introduced for prime differential ideals. For an irreducible closed set 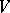 in a differential affine space, i.e. in an affine space over a universal extension
in a differential affine space, i.e. in an affine space over a universal extension 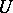 of the field of coefficients, one defines a differential dimension polynomial
of the field of coefficients, one defines a differential dimension polynomial
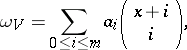 |
where 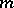 is the number of differentiations in
is the number of differentiations in 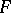 . The coefficient
. The coefficient  is known as the differential dimension of
is known as the differential dimension of 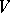 , the degree
, the degree 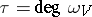 of the polynomial is known as the differential type of the set
of the polynomial is known as the differential type of the set 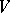 , while the coefficient
, while the coefficient 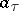 is called its typical differential dimension. The polynomial
is called its typical differential dimension. The polynomial 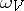 is a birational invariant, but is not a differential birational invariant. This is the case for
is a birational invariant, but is not a differential birational invariant. This is the case for 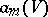 ,
, 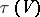 and
and 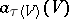 . The determination of differential birational invariants is of major interest. Another problem is to estimate the possible values of the invariants obtained. Let
. The determination of differential birational invariants is of major interest. Another problem is to estimate the possible values of the invariants obtained. Let 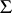 be a set in
be a set in 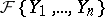 . If the orders of the elements of
. If the orders of the elements of 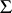 are bounded, then the differential dimension polynomials of the components of
are bounded, then the differential dimension polynomials of the components of 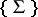 are subject to certain restrictions. In particular, if for each
are subject to certain restrictions. In particular, if for each 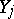 the order of any element of
the order of any element of 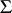 with respect to
with respect to 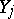 does not exceed
does not exceed 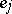 , it follows from the condition
, it follows from the condition 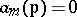 that, for any component of the variety
that, for any component of the variety 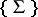 , one has
, one has 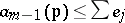 . The hypothesis in the general case is
. The hypothesis in the general case is
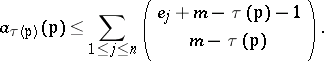 |
This hypothesis is not valid, as was shown by M. Kondrat'eva. If the set 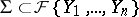 consists of
consists of  differential polynomials
differential polynomials 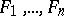 , two additional hypotheses are also postulated. Let
, two additional hypotheses are also postulated. Let
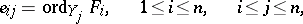 |
and
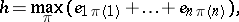 |
where 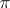 runs through the symmetric group
runs through the symmetric group  . The first hypothesis states that for any component
. The first hypothesis states that for any component 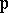 of the variety
of the variety 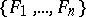 it follows from
it follows from 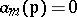 that
that 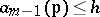 . This statement has been proved in a number of special cases. According to the second hypothesis, for any component
. This statement has been proved in a number of special cases. According to the second hypothesis, for any component 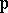 of the variety
of the variety 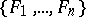 it follows from
it follows from 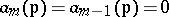 that
that 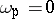 . This hypothesis has been proved.
. This hypothesis has been proved.
A difficult problem in differential algebra is the decomposition of a differential algebraic variety into irreducible components. Even if 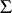 consists of a single irreducible differential polynomial
consists of a single irreducible differential polynomial 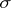 the corresponding variety usually consists of several components, one of which contains all non-singular solutions of the equation
the corresponding variety usually consists of several components, one of which contains all non-singular solutions of the equation 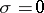 (and may also contain singular solutions), while all the remaining components consist of solutions in which any separant of the differential polynomial
(and may also contain singular solutions), while all the remaining components consist of solutions in which any separant of the differential polynomial 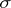 vanishes. The case of a hypersurface (a system
vanishes. The case of a hypersurface (a system 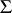 of one equation) is especially important, since any differential algebraic variety over an ordinary differential field is differentially birationally isomorphic to a hypersurface.
of one equation) is especially important, since any differential algebraic variety over an ordinary differential field is differentially birationally isomorphic to a hypersurface.
Since any prime differential ideal is completely defined by its characteristic set, one may subdivide the problem of the decomposition of a differential algebraic variety 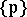 into two parts: 1) to find a finite set
into two parts: 1) to find a finite set 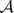 of autoreduced subsets of
of autoreduced subsets of 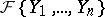 each of which is a characteristic set of a prime differential ideal containing
each of which is a characteristic set of a prime differential ideal containing 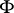 such that
such that 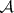 contains a characteristic set of each component of
contains a characteristic set of each component of 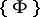 ; 2) to determine, for a given autoreduced set in
; 2) to determine, for a given autoreduced set in 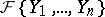 whether or not it is a characteristic set of any component of
whether or not it is a characteristic set of any component of 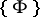 .
.
The solution of 2) is not known (1987) in the general case, but the important special case when 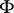 consists of one differential polynomial can be solved with the aid of two theorems of Ritt: The component theorem and the low power theorem (see below).
consists of one differential polynomial can be solved with the aid of two theorems of Ritt: The component theorem and the low power theorem (see below).
The problem of finding the components of the variety 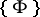 may also be decomposed into problem 1) and the following problem: 3) to determine, for given characteristic sets
may also be decomposed into problem 1) and the following problem: 3) to determine, for given characteristic sets 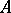 and
and 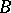 of prime differential ideals
of prime differential ideals 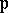 and
and 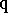 respectively, if the inclusion
respectively, if the inclusion 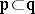 holds.
holds.
Problem 3) is also still far from being solved. In the particular case when 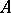 consists of one irreducible differential polynomial
consists of one irreducible differential polynomial  and
and 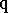 is a differential ideal
is a differential ideal 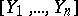 , the problem is to find whether or not the point
, the problem is to find whether or not the point 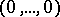 is comprised in the general solution of the differential equation
is comprised in the general solution of the differential equation 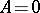 .
.
Problem 1) has been solved, "in principle" , for a finite set 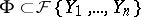 : An inductive procedure (the theory of elimination for systems of algebraic differential equations) converts it to a number of "easier" problems involving polynomials in a finite number of unknowns over
: An inductive procedure (the theory of elimination for systems of algebraic differential equations) converts it to a number of "easier" problems involving polynomials in a finite number of unknowns over 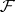 , i.e. a problem involving algebraic differential equations is reduced to one involving algebraic equations.
, i.e. a problem involving algebraic differential equations is reduced to one involving algebraic equations.
The components theorem says that the singular components are in their turn generic components of other differential polynomials. More exactly, let 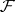 be a differential field and let
be a differential field and let 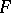 denote a non-zero differential polynomial in
denote a non-zero differential polynomial in 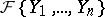 . If
. If 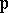 is some component of the ideal
is some component of the ideal 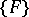 of the ring
of the ring 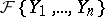 , then there exists an irreducible differential polynomial
, then there exists an irreducible differential polynomial 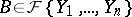 such that
such that 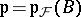 is a generic component of the variety
is a generic component of the variety 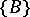 .
.
The low power theorem provides a criterion for determining whether or not the component of an irreducible differential polynomial 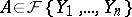 is a component of
is a component of 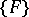 . More exactly, let
. More exactly, let 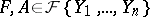 , let the orders of
, let the orders of 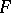 and
and 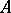 with respect to
with respect to 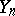 be equal to
be equal to 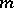 and
and 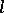 , respectively, let
, respectively, let 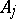 be the
be the 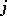 -th derivative of
-th derivative of 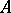 and let
and let 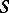 be the separant of
be the separant of 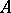 . There exist a
. There exist a 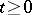 and an
and an 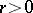 such that
such that
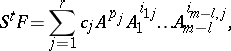 |
where 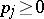 ,
, 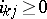 , no two sets
, no two sets  coincide, the order of
coincide, the order of 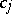 with respect to
with respect to 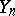 does not exceed
does not exceed 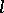 , and
, and 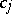 is not divisible by
is not divisible by 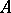 . If such a decomposition has been found, the low power theorem states that a generic component of the variety
. If such a decomposition has been found, the low power theorem states that a generic component of the variety 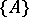 is a component of the variety
is a component of the variety 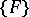 if and only if the decomposition, when written out, contains a term
if and only if the decomposition, when written out, contains a term 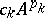 which does not contain derivatives of
which does not contain derivatives of 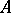 and the degree of which is lower than the degree of any other term in the decomposition, regarded as a polynomial in
and the degree of which is lower than the degree of any other term in the decomposition, regarded as a polynomial in 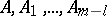 (if the characteristic is non-zero, this condition is neither necessary nor sufficient).
(if the characteristic is non-zero, this condition is neither necessary nor sufficient).
The second trend of studies in differential algebra concerns the problem of extensions of specializations. Let 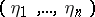 and
and 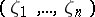 be points in
be points in 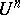 , where
, where 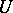 is a universal extension of a differential field
is a universal extension of a differential field 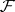 . A point
. A point 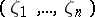 is said to be a differential specialization of the point
is said to be a differential specialization of the point 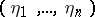 over
over 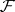 (this is denoted by
(this is denoted by  ) if any differential polynomial which vanishes in
) if any differential polynomial which vanishes in  also vanishes in
also vanishes in 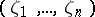 . If
. If 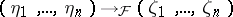 and
and 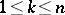 , it is clear that
, it is clear that 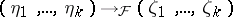 . One says that the first specialization is an extension of the second.
. One says that the first specialization is an extension of the second.
Let 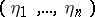 and
and 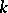 be given, and let
be given, and let 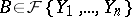 be such that
be such that 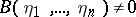 . It can be shown that there exists a non-zero differential polynomial
. It can be shown that there exists a non-zero differential polynomial 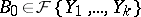 satisfying the condition
satisfying the condition 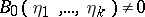 such that any differential specialization
such that any differential specialization 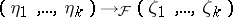 for which
for which 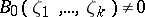 may be extended to a differential specialization
may be extended to a differential specialization 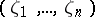 where
where 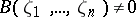 . However, unlike the situation in algebraic geometry, a differential specialization
. However, unlike the situation in algebraic geometry, a differential specialization 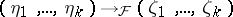 cannot always be extended to a differential specialization
cannot always be extended to a differential specialization 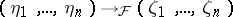 , even if the elements
, even if the elements 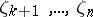 assume the value
assume the value 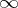 . Thus, the resulting problem is to find a criterion for the possibility of an extension of a specialization
. Thus, the resulting problem is to find a criterion for the possibility of an extension of a specialization 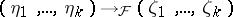 to a differential specialization
to a differential specialization 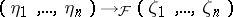 .
.
A special case of this problem is encountered in the problem of indeterminate forms. Let the polynomials 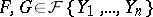 be relatively prime, let
be relatively prime, let 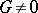 , and let
, and let 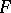 and
and 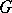 vanish at
vanish at 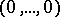 . The problem is to assign to the ratio
. The problem is to assign to the ratio 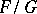 a value at the point
a value at the point 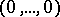 . Let the elements
. Let the elements 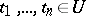 be differentially algebraically independent over
be differentially algebraically independent over 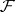 and let
and let
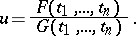 |
It is natural to say that 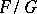 admits the value
admits the value 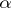 at
at 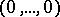 if
if 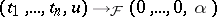 . Thus, the problem is reduced to finding the extensions of
. Thus, the problem is reduced to finding the extensions of 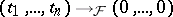 to
to 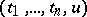 . This is equivalent to determining the elements
. This is equivalent to determining the elements 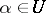 such that
such that 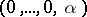 is a zero of the generic component of the differential polynomial
is a zero of the generic component of the differential polynomial 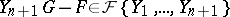 . J.F. Ritt conjectured that
. J.F. Ritt conjectured that 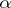 is either uniquely defined (possibly equal to
is either uniquely defined (possibly equal to 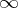 ) or else is completely arbitrary; he proved this conjecture for ordinary differential fields for
) or else is completely arbitrary; he proved this conjecture for ordinary differential fields for 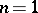 ,
, 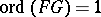 . Studies are made of the properties of concrete differential ideals in the ring
. Studies are made of the properties of concrete differential ideals in the ring 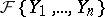 . In the case of an infinite sequence
. In the case of an infinite sequence 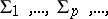 of prime differential ideals in
of prime differential ideals in 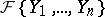 , where each
, where each 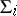 is a proper divisor of
is a proper divisor of 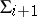 , the intersection of all
, the intersection of all 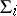 is a prime differential ideal and the dimension of the corresponding variety
is a prime differential ideal and the dimension of the corresponding variety 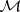 is higher than that of the variety
is higher than that of the variety 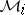 corresponding to
corresponding to 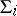 for an arbitrary
for an arbitrary 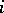 .
.
Of the other results concerning differential algebraic varieties, the analogue of Lüroth's theorem is worth mentioning: If 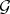 is an extension of a differential field
is an extension of a differential field 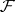 contained in
contained in 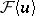 , then
, then 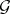 contains an element
contains an element  such that
such that 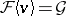 .
.
However, the theory of differential algebraic curves (varieties of differential dimension 1) is only in its initial stage of development; even for invariants such as the genus of the curve in algebraic geometry, differential algebraic analogues have not been found. Of major interest is the intersection theory of differential algebraic varieties. The theorem that the intersection of two irreducible varieties of dimensions 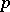 and
and 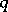 in
in  -dimensional affine space has dimension
-dimensional affine space has dimension 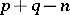 or higher is not valid for these varieties. However, differential algebraic varieties are characterized not only by the dimension but also by their order with respect to a chosen differential transcendence basis. A number of estimates from above have been obtained for the intersection order of varieties with respect to a specially chosen basis. The following analytic theorem on the intersection of components of the same differential polynomial has been proved: If
or higher is not valid for these varieties. However, differential algebraic varieties are characterized not only by the dimension but also by their order with respect to a chosen differential transcendence basis. A number of estimates from above have been obtained for the intersection order of varieties with respect to a specially chosen basis. The following analytic theorem on the intersection of components of the same differential polynomial has been proved: If 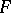 is a differential polynomial in the unknowns
is a differential polynomial in the unknowns 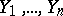 , then in a zero of the polynomial
, then in a zero of the polynomial 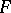 contained in more than one component of
contained in more than one component of 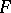 the derivative
the derivative 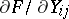 vanishes for
vanishes for 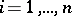 and arbitrary
and arbitrary 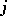 . The concept of a differential algebraic variety may be generalized (dropping the assumption that it is affine). In particular, it is possible to introduce the concepts of differentially homogeneous polynomials and of projective differential algebraic varieties.
. The concept of a differential algebraic variety may be generalized (dropping the assumption that it is affine). In particular, it is possible to introduce the concepts of differentially homogeneous polynomials and of projective differential algebraic varieties.
For a differential field 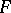 there is no differential algebraic closure, and differential algebraically closed fields do not exist. They are replaced, in a sense, by the so-called "constrained" extensions.
there is no differential algebraic closure, and differential algebraically closed fields do not exist. They are replaced, in a sense, by the so-called "constrained" extensions.
The Galois theory of differential fields represents a trend in differential algebra. A universal differential extension 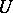 of a differential field
of a differential field 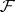 is constructed and the set of differential isomorphisms from a finitely-generated differential algebraic extension
is constructed and the set of differential isomorphisms from a finitely-generated differential algebraic extension 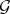 of the field
of the field 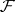 into
into 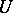 which are the identity on
which are the identity on 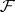 are considered. If
are considered. If 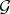 is a strongly normal extension of
is a strongly normal extension of  , it is possible to introduce the structure of an algebraic group over the field
, it is possible to introduce the structure of an algebraic group over the field 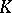 (of constants of
(of constants of 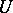 ) on the set
) on the set 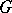 of differential isomorphisms from
of differential isomorphisms from 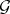 into
into 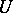 . A special case of strongly normal extensions are the Picard–Vessiot extensions, obtained by adding to the field
. A special case of strongly normal extensions are the Picard–Vessiot extensions, obtained by adding to the field 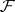 the solutions of a linear homogeneous differential equation with coefficients in
the solutions of a linear homogeneous differential equation with coefficients in 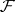 . The Galois group of a Picard–Vessiot extension is an algebraic matrix group. The correspondence between the intermediate fields and the subgroups of the group
. The Galois group of a Picard–Vessiot extension is an algebraic matrix group. The correspondence between the intermediate fields and the subgroups of the group 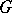 is described by the following theorem.
is described by the following theorem.
Let 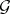 be a strongly normal extension of a differential field
be a strongly normal extension of a differential field 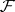 with field of constants
with field of constants 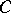 . a) If
. a) If 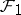 is a differential field such that
is a differential field such that 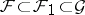 , then
, then 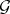 is strongly normal over
is strongly normal over 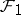 , the Galois group
, the Galois group 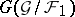 is a
is a  -subgroup in
-subgroup in 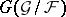 and the field of invariants of
and the field of invariants of 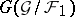 in
in  coincides with
coincides with 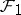 . b) If
. b) If 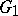 is a
is a 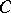 -subgroup of
-subgroup of 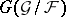 and
and 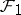 denotes the set of invariants of the group
denotes the set of invariants of the group 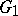 in
in 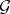 , then
, then 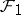 is a differential field,
is a differential field, 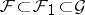 and
and 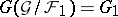 .
.
The normal subgroups  of
of 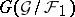 correspond to strongly normal extensions
correspond to strongly normal extensions 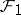 of
of 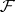 and vice versa. The inverse Galois problem — that is, the problem of the existence of a strongly normal extension
and vice versa. The inverse Galois problem — that is, the problem of the existence of a strongly normal extension 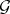 of a field
of a field 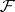 the Galois group
the Galois group 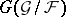 of which is isomorphic to a given group — has been solved for connected solvable groups. The problem was reduced to an estimate of the dimension of some vector space over the field of constants
of which is isomorphic to a given group — has been solved for connected solvable groups. The problem was reduced to an estimate of the dimension of some vector space over the field of constants 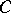 of
of 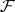 and the rank of a certain Abelian group. Results on the Galois theory of infinite extensions are available. The theory of integration in finite form deals with problems related to Galois theory.
and the rank of a certain Abelian group. Results on the Galois theory of infinite extensions are available. The theory of integration in finite form deals with problems related to Galois theory.
The theory of differential algebraic groups, substantially different from its algebraic analogue, is in the course of development. In particular, the differential ring of everywhere-defined differential rational functions on an affine differential algebraic set is not a differential coordinate ring and, in general, is not finitely generated as a differential algebra.
The analogue of Liouville's theorem on the approximation of algebraic numbers by rational numbers may be mentioned as a result obtained for the approximation of differential algebraic functions by differential rational functions. However, the analogue of the Thue–Siegel–Roth theorem has not yet (1987) been proved.
The theory of rings with higher differentiations is now being developed. Higher differentiations are a strong tool in the study of objects of non-zero characteristic. If the characteristic of the differential ring 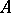 is
is 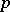 , the
, the 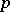 -th power of any element is constant; this is not true of rings with higher differentiations. Analogues of many results listed above, concerning both the intersection theory of ideals and Galois theory, have been obtained for rings with higher differentiations.
-th power of any element is constant; this is not true of rings with higher differentiations. Analogues of many results listed above, concerning both the intersection theory of ideals and Galois theory, have been obtained for rings with higher differentiations.
References
| [1] | I. Kaplansky, "An introduction to differential algebra" , Hermann (1957) |
| [2] | J.F. Ritt, "Differential algebra" , Amer. Math. Soc. (1950) |
| [3] | E.R. Kolchin, "Differential algebra and algebraic groups" , Acad. Press (1973) |
| [4] | E.R. Kolchin, "Some problems in differential algebra" , Proc. Internat. Congress Mathematicians (Moscow, 1966) , Mir (1968) pp. 269–276 |
Comments
For the notion of dimension polynomial of an extension of differential fields cf. Dimension polynomial. Universal extensions of a differential field, a substitute for the algebraic geometric notion of a universal (i.e. large enough algebraically closed) extension of the base field 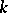 one is working over, are discussed in Extension of a differential field. The various other notions of differential algebra which occur in the main article above are described below.
one is working over, are discussed in Extension of a differential field. The various other notions of differential algebra which occur in the main article above are described below.
Let 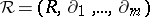 be a differential ring consisting of the commutative ring with unit element
be a differential ring consisting of the commutative ring with unit element 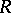 and the commuting derivations
and the commuting derivations 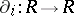 ,
, 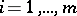 . A differential ideal of
. A differential ideal of 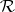 is an ideal
is an ideal 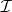 of
of 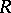 such that
such that 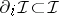 for all
for all 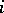 . Let
. Let 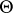 denote the free commutative semi-group generated by the
denote the free commutative semi-group generated by the 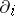 ,
, 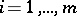 . The elements of
. The elements of 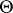 are called the derivative operators of
are called the derivative operators of 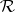 . If
. If 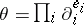 , the order of
, the order of 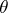 is
is 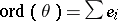 .
.
Now consider a set 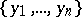 of differential indeterminates over
of differential indeterminates over 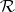 (i.e. the
(i.e. the  are differentiably algebraically independent over
are differentiably algebraically independent over 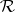 , cf. Extension of a differential field). A ranking of
, cf. Extension of a differential field). A ranking of 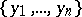 is a total order on the set of all derivatives
is a total order on the set of all derivatives 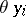 ,
, 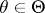 , that satisfies for all such derivatives
, that satisfies for all such derivatives 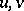 the conditions:
the conditions: 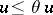 and
and 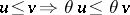 , for all
, for all 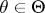 . Let
. Let 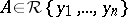 , the ring of differential polynomials in
, the ring of differential polynomials in  over
over 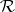 . The highest ranking derivative
. The highest ranking derivative 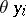 present in
present in 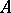 is called the leader of the differential polynomial
is called the leader of the differential polynomial 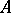 ; it will be denoted by
; it will be denoted by 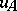 . Let
. Let 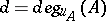 , then
, then 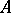 can be written in the form
can be written in the form 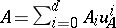 where the
where the 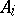 are in
are in 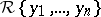 and do not contain
and do not contain 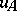 (or any higher ranking derivative). The differential polynomial
(or any higher ranking derivative). The differential polynomial 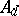 is called the initial differential polynomial of
is called the initial differential polynomial of 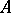 and the differential polynomial
and the differential polynomial 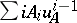 (
(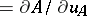 ) is called the separant of
) is called the separant of 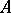 . All these notions are dependent on the ranking used. It is useful to extent the total order on the
. All these notions are dependent on the ranking used. It is useful to extent the total order on the 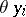 to a comparative rank on all elements of
to a comparative rank on all elements of  . This is done as follows.
. This is done as follows.
a) Every element of 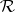 has lower rank than every element of
has lower rank than every element of 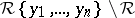 .
.
b) Let  . If
. If 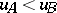 (or
(or  and
and 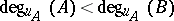 ), then
), then 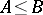 .
.
c) All elements in 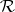 have the same rank.
have the same rank.
d) If  and
and 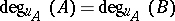 , then
, then 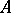 and
and 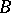 have the same rank. Different differential polynomials may of course have the same rank but this does define in any case a partial order on
have the same rank. Different differential polynomials may of course have the same rank but this does define in any case a partial order on 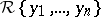 .
.
Let 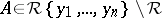 and let
and let 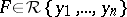 . The differential polynomial
. The differential polynomial 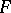 is called partially reduced with respect to
is called partially reduced with respect to 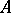 if
if 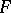 contains no proper derivative of
contains no proper derivative of 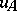 (i.e. contains no
(i.e. contains no 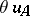 ,
, 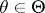 ). If, moreover,
). If, moreover, 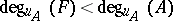 ,
, 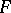 is said to be reduced with respect to
is said to be reduced with respect to 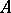 . More generally,
. More generally, 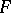 is said to be reduced with respect to a subset
is said to be reduced with respect to a subset 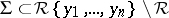 if
if 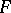 is reduced with respect to every member of
is reduced with respect to every member of 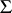 . A subset
. A subset 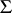 of
of 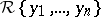 is said to be autoreduced if
is said to be autoreduced if  and if each element
and if each element 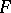 of
of 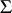 is reduced with respect to
is reduced with respect to 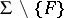 . Every autoreduced set is finite. These sets were introduced by Ritt (who called them ascending sets or chains) as a tool in his process of reduction of differential polynomials. This process plays a role analogous to Euclidean division (with remainder) for ordinary polynomials.
. Every autoreduced set is finite. These sets were introduced by Ritt (who called them ascending sets or chains) as a tool in his process of reduction of differential polynomials. This process plays a role analogous to Euclidean division (with remainder) for ordinary polynomials.
The notion of comparative rank of elements of 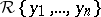 is extended to a ranking of autoreduced subsets of
is extended to a ranking of autoreduced subsets of 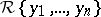 as follows. Let
as follows. Let 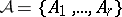 and
and 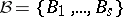 be autoreduced subsets of
be autoreduced subsets of 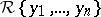 , where both
, where both 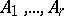 and
and 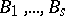 are arranged in orders of increasing rank.
are arranged in orders of increasing rank.
e) If there exists a 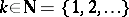 ,
, 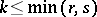 , such that
, such that 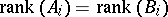 ,
, 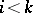 and
and 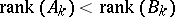 , then
, then 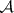 has lower rank than
has lower rank than 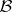 .
.
f) If 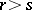 and
and 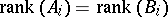 ,
, 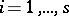 , then
, then  has lower rank than
has lower rank than 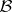 .
.
g) If  and
and 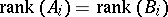 ,
, 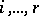 , then
, then 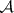 and
and 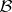 have the same rank.
have the same rank.
Now let  be a differential ideal in
be a differential ideal in 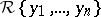 . Then there exists an autoreduced set
. Then there exists an autoreduced set 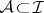 such that the separant
such that the separant 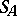 of
of 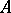 is not in
is not in 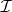 for all
for all 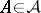 . Such an autoreduced subset of lowest rank of
. Such an autoreduced subset of lowest rank of 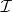 is called a characteristic set of
is called a characteristic set of 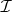 .
.
Consider again a differential polynomial 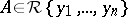 . If there is a
. If there is a 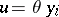 ,
, 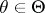 , such that
, such that 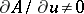 , then there is such a
, then there is such a  of maximal order. This order is called the essential order of
of maximal order. This order is called the essential order of 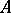 . There is then also such a
. There is then also such a  (such that
(such that 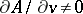 ) of highest rank. If, moreover,
) of highest rank. If, moreover, 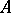 does not contain any proper derivative of
does not contain any proper derivative of  , then
, then  is called the pseudo-leader of
is called the pseudo-leader of 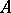 (relative to the given ranking); the pseudo-separant of
(relative to the given ranking); the pseudo-separant of 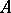 is then
is then 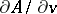 . (If
. (If  for all
for all 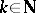 ,
, 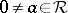 , then the notions of pseudo-leader and pseudo-separant of course coincide with those of leader and separant, but if
, then the notions of pseudo-leader and pseudo-separant of course coincide with those of leader and separant, but if 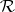 is of characteristic
is of characteristic 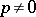 , e.g., this need not be the case.)
, e.g., this need not be the case.)
Let 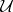 be a universal extension of
be a universal extension of 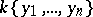 , where
, where  is a differential field. Let
is a differential field. Let 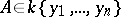 . A point
. A point 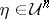 is called a non-singular zero of
is called a non-singular zero of 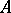 , or a non-singular solution of
, or a non-singular solution of 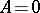 , if
, if 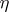 is a zero of
is a zero of 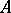 and there exists a ranking of
and there exists a ranking of 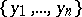 relative to which
relative to which 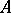 is pseudo-led and such that the corresponding pseudo-separant does not vanish at
is pseudo-led and such that the corresponding pseudo-separant does not vanish at 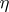 . The order zeros of
. The order zeros of 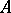 (solutions of
(solutions of 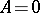 ) are called singular zeros (singular solutions).
) are called singular zeros (singular solutions).
Differential algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_algebra&oldid=15882