Differential-geometric structure

One of the fundamental concepts in modern differential geometry including the specific structures studied in classical differential geometry. It is defined for a given differentiable manifold 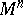as a differentiable section in a fibre space 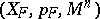with base 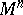associated with a certain principal bundle 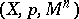or, according to another terminology, as a differentiable field of geometric objects on 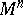. Here 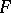is some differentiable 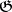-space where 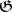is the structure Lie group of the principal bundle or, in another terminology, the representation space of the Lie group .

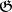If 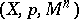is the principal bundle of frames in the tangent space to , 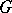is some closed subgroup in 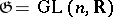, and 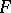is the homogeneous space 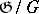, the corresponding differential-geometric structure on 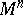is called a -structure or an infinitesimal structure of the first order. For example, if 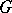consists of those linear transformations (elements of 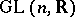) which leave an 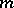-dimensional space in 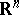invariant, the corresponding 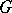-structure defines a distribution of 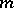-dimensional subspaces on 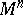. If 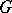is the orthogonal group 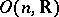— the subgroup of elements of 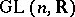which preserve the scalar product in 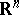—, then the -structure is a Riemannian metric on 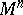, i.e. the field of a positive-definite symmetric tensor 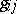. In a similar manner, almost-complex and complex structures are special cases of 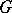-structures on 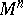. 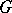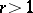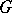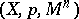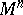A generalization of the concept of a -structure is an infinitesimal structure of order , (or -structure of a higher order); here is the principal bundle of frames of the order on , and 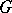is a closed subgroup of its structure group .

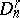All kinds of connections (cf. Connection) are important special cases of differential-geometric structures. For instance, a connection in a principal bundle is obtained if the role of 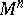is played by the space of some principal bundle 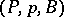, and the 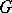-structure on 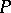is the distribution of 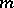-dimensional, 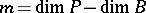, subspaces complementary to the tangent spaces of the fibres which is invariant with respect to the action on 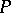of the structure group of the bundle. Connections on a manifold 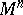are special cases of differential-geometric structures on 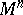, but more general ones than 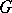-structures on 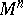. 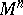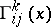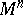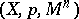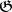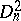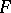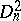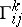For instance, an affine connection on , definable by a field of connection objects , is obtained as the differential-geometric structure on for which is the principal bundle of frames of second order, is its structure group , and the representation space of is the space with coordinates , where the representation is defined by the formulas

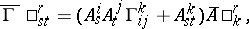where

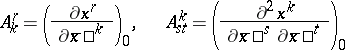are the coordinates of an element of the group 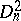, and 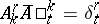. In the case of a projective connection on 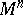one deals with a certain representation of 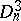in 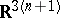, while in cases of connections of a higher order, one deals with representations of 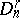. By this approach the theory of differential-geometric structures becomes closely related to the theory of geometric objects (Cf. Geometric objects, theory of).

References

[1]	O. Veblen, J.H.C. Whitehead, "The foundations of differential geometry" , Cambridge Univ. Press (1932) (Appendix by V.V. Vagner in the Russian translation)
[2]	G.F. Laptev, "Differential geometry of imbedded manifolds. Group-theoretical method of differential geometric investigation" Trudy Moskov. Mat. Obshch. , 2 (1953) pp. 275–382 (In Russian)
[3]	D. Husemoller, "Fibre bundles" , McGraw-Hill (1966)
[4]	S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964)

References

[a1]	M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish (1972–1975) pp. 1–5