Differential
The main linear part of increment of a function.
1) A real-valued function 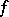 of a real variable
of a real variable  is said to be differentiable at a point
is said to be differentiable at a point  if it is defined in some neighbourhood of this point and if there exists a number
if it is defined in some neighbourhood of this point and if there exists a number 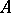 such that the increment
such that the increment
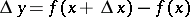 |
may be written (if the point 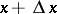 lies in this neighbourhood) in the form
lies in this neighbourhood) in the form
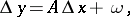 |
where 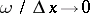 as
as 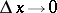 . Here
. Here  is usually denoted by
is usually denoted by 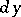 and is called the differential of
and is called the differential of 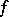 at
at  . For a given
. For a given  the differential
the differential 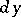 is proportional to
is proportional to 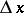 , i.e. is a linear function of
, i.e. is a linear function of 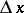 . By definition, as
. By definition, as 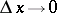 the additional term
the additional term 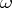 is infinitely small of a higher order than
is infinitely small of a higher order than 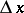 (and also than
(and also than 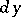 if
if 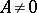 ). This is why the differential is said to be the main part of increment of the function.
). This is why the differential is said to be the main part of increment of the function.
For a function which is differentiable at a point  ,
, 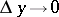 if
if 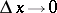 , i.e. a function which is differentiable at a point is continuous at that point. A function
, i.e. a function which is differentiable at a point is continuous at that point. A function 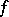 is differentiable at a point
is differentiable at a point  if and only if it has, at that point, a finite derivative
if and only if it has, at that point, a finite derivative
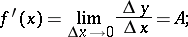 |
moreover,
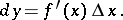 |
There exist continuous functions which are not differentiable.
The designation 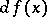 may be used instead of
may be used instead of 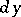 , and the above equation assumes the form
, and the above equation assumes the form
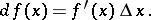 |
The increment of the argument 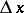 is then usually denoted by
is then usually denoted by 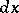 , and is said to be the differential of the independent variable. Accordingly, one may write
, and is said to be the differential of the independent variable. Accordingly, one may write
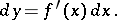 |
Hence 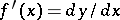 , i.e. the derivative is equal to the ratio of the differentials
, i.e. the derivative is equal to the ratio of the differentials 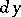 and
and 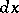 . If
. If 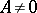 , then
, then 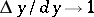 as
as 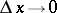 , i.e. if
, i.e. if 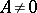 , then
, then 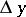 and
and 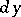 are infinitesimals of the same order as
are infinitesimals of the same order as 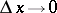 ; this fact, along with the simple structure of the differential (i.e. linearity with respect to
; this fact, along with the simple structure of the differential (i.e. linearity with respect to 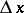 ), is often used in approximate computations, by assuming that
), is often used in approximate computations, by assuming that 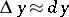 for small
for small 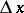 . E.g., if it is desired to compute
. E.g., if it is desired to compute 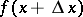 from a known
from a known 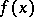 when
when 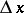 is small, it is assumed that
is small, it is assumed that
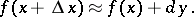 |
Obviously, such reasoning is useful only if it is possible to estimate the magnitude of the error involved.
Geometric interpretation of the differential. The equation of the tangent to the graph of a function 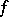 at a point
at a point 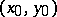 is of the form
is of the form 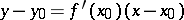 . If one puts
. If one puts 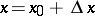 , then
, then 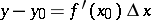 . The right-hand side represents the value of the differential of the function
. The right-hand side represents the value of the differential of the function 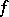 at the point
at the point 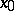 corresponding to the value of
corresponding to the value of 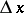 being considered. Thus, the differential is identical with the corresponding increment of the ordinate of the tangent to the curve
being considered. Thus, the differential is identical with the corresponding increment of the ordinate of the tangent to the curve 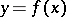 (cf. the segment
(cf. the segment 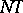 in Fig. a). Here
in Fig. a). Here 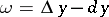 , i.e. the value of
, i.e. the value of 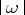 coincides with the length of the segment
coincides with the length of the segment 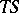 .
.
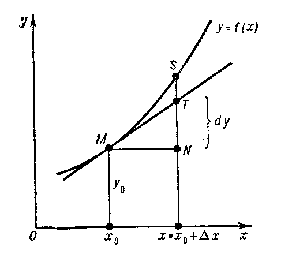
Figure: d031810a
2) The definitions of differentiability and differential are readily extended to real-valued functions of  real variables. Thus, in the case
real variables. Thus, in the case 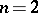 a real-valued function is said to be differentiable at a point
a real-valued function is said to be differentiable at a point 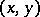 with respect to both variables
with respect to both variables  and
and 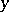 if it is defined in some neighbourhood of this point and if its total increment
if it is defined in some neighbourhood of this point and if its total increment
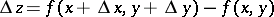 |
may be written as
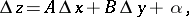 |
where 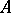 and
and 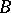 are real numbers,
are real numbers, 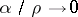 if
if 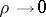 ,
, 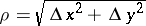 ; it is assumed that the point
; it is assumed that the point 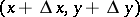 belongs to the neighbourhood mentioned above (Fig. b).
belongs to the neighbourhood mentioned above (Fig. b).
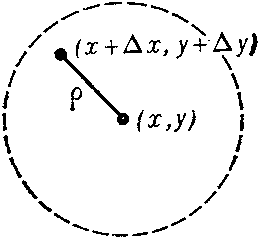
Figure: d031810b
One introduces the notation
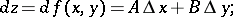 |
 is said to be the total differential, or simply the differential, of the function
is said to be the total differential, or simply the differential, of the function 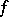 at the point
at the point 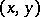 (the phrase "with respect to both variables x and y" is sometimes added). For a given point
(the phrase "with respect to both variables x and y" is sometimes added). For a given point 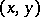 the differential
the differential 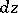 is a linear function of
is a linear function of 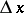 and
and 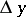 ; the difference
; the difference 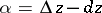 is infinitely small of a higher order than
is infinitely small of a higher order than 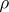 . In this sense
. In this sense 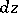 is the main linear part of the increment
is the main linear part of the increment 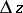 .
.
If 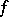 is differentiable at the point
is differentiable at the point 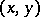 , then it is continuous at this point and has finite partial derivatives (cf. Derivative)
, then it is continuous at this point and has finite partial derivatives (cf. Derivative)
 |
at this point. Thus
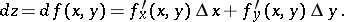 |
The increments 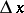 and
and 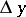 of the independent variables are usually denoted by
of the independent variables are usually denoted by 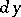 and
and 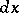 , as in the case of a single variable. One may write, accordingly,
, as in the case of a single variable. One may write, accordingly,
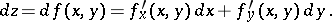 |
The existence of finite partial derivatives does not, in general, entail the differentiability of the function (even if it is assumed to be continuous).
If a function 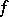 has a partial derivative with respect to
has a partial derivative with respect to  at a point
at a point 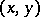 , the product
, the product 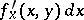 is said to be its partial differential with respect to
is said to be its partial differential with respect to  ; in the same manner,
; in the same manner, 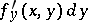 is the partial differential with respect to
is the partial differential with respect to 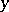 . If the function is differentiable, its total differential is equal to the sum of the partial differentials. Geometrically, the total differential
. If the function is differentiable, its total differential is equal to the sum of the partial differentials. Geometrically, the total differential 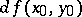 is the increment in the
is the increment in the  -direction in the tangent plane to the surface
-direction in the tangent plane to the surface 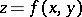 at the point
at the point 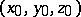 , where
, where 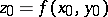 (Fig. c).
(Fig. c).
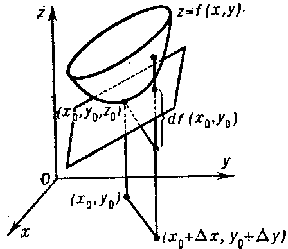
Figure: d031810c
The following is a sufficient criterion for the differentiability of a function: If in a certain neighbourhood of a point 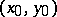 a function
a function 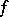 has a partial derivative
has a partial derivative 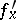 which is continuous at
which is continuous at 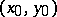 and, in addition, has a partial derivative
and, in addition, has a partial derivative 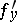 at that point, then
at that point, then 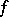 is differentiable at that point.
is differentiable at that point.
If a function 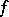 is differentiable at all points of an open domain
is differentiable at all points of an open domain 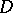 , then at any point of the domain
, then at any point of the domain
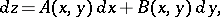 |
where 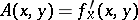 ,
, 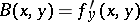 . If, in addition, there exist continuous partial derivatives
. If, in addition, there exist continuous partial derivatives 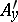 and
and 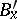 in
in 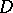 , then, everywhere in
, then, everywhere in 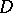 ,
,
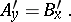 |
This proves, in particular, that not every expression
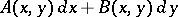 |
with continuous 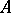 and
and 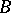 (in a domain
(in a domain 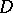 ) is the total differential of some function of two variables. This is a difference from functions of one variable, where any expression
) is the total differential of some function of two variables. This is a difference from functions of one variable, where any expression 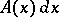 with a continuous function
with a continuous function  in some interval is the differential of some function.
in some interval is the differential of some function.
The expression 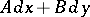 is the total differential of some function
is the total differential of some function 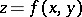 in a simply-connected open domain
in a simply-connected open domain 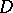 if
if 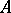 and
and 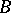 are continuous in this domain, meet the condition
are continuous in this domain, meet the condition 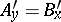 and, in addition: a)
and, in addition: a) 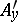 and
and 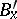 are continuous or b)
are continuous or b) 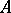 and
and 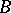 are everywhere differentiable in
are everywhere differentiable in 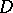 with respect to both variables
with respect to both variables  and
and 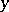 [7], [8].
[7], [8].
See also Differential calculus for differentials of real-valued functions of one or more real variables and for differentials of higher orders.
3) Let a function 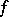 be defined on some set
be defined on some set 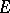 of real numbers, let
of real numbers, let  be a limit point of this set, let
be a limit point of this set, let 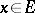 ,
, 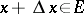 ,
, 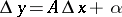 , where
, where 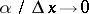 if
if 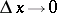 ; then the function
; then the function 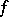 is called differentiable with respect to the set
is called differentiable with respect to the set 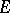 at
at  , while
, while 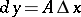 is called its differential with respect to the set
is called its differential with respect to the set 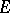 at
at  . This is a generalization of the differential of a real-valued function of one real variable. Special kinds of this generalization include differentials at the end points of the interval within which the function is defined, and the approximate differential (cf. Approximate differentiability).
. This is a generalization of the differential of a real-valued function of one real variable. Special kinds of this generalization include differentials at the end points of the interval within which the function is defined, and the approximate differential (cf. Approximate differentiability).
Differentials with respect to a set for real-valued functions of several real variables are introduced in a similar manner.
4) All definitions of differentiability and a differential given above can be extended, almost unchanged, to complex-valued functions of one or more real variables; to real-valued and complex-valued vector-functions of one or more real variables; and to complex functions and vector-functions of one or more complex variables. In functional analysis they are extended to functions of the points of an abstract space. One may speak of differentiability and of the differential of a set function with respect to some measure.
References
| [1] | G.P. Tolstov, "Elements of mathematical analysis" , 1–2 , Moscow (1974) (In Russian) |
| [2] | G.M. Fichtenholz, "Differential und Integralrechnung" , 1 , Deutsch. Verlag Wissenschaft. (1964) |
| [3] | L.D. Kudryavtsev, "Mathematical analysis" , 1 , Moscow (1973) (In Russian) |
| [4] | S.M. Nikol'skii, "A course of mathematical analysis" , 1 , MIR (1977) (Translated from Russian) |
| [5] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
| [6] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [7] | G.P. Tolstov, "On curvilinear and iterated integrals" Trudy Mat. Inst. Steklov. , 35 (1950) (In Russian) |
| [8] | G.P. Tolstov, "On the total differential" Uspekhi Mat. Nauk , 3 : 5 (1948) pp. 167–170 |
Comments
See also Differentiation; Differentiation of a mapping.
For differentiation of set functions cf. Set function; Radon–Nikodým theorem, [a7].
For generalizations to functions between abstract spaces see also Fréchet derivative; Gâteaux derivative.
For the derivative of a function 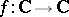 see Analytic function.
see Analytic function.
References
| [a1] | T.M. Apostol, "Calculus" , 1–2 , Blaisdell (1964) |
| [a2] | T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1974) |
| [a3] | W. Fleming, "Functions of several variables" , Springer (1977) |
| [a4] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) |
| [a5] | R. Courant, "Vorlesungen über Differential- und Integralrechnung" , 1–2 , Springer (1971–1972) |
| [a6] | I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian) |
| [a7] | G.E. Shilov, B.L. Gurevich, "Integral, measure, and derivative: a unified approach" , Dover, reprint (1977) (Translated from Russian) |
| [a8] | A. Denjoy, "Introduction à la théorie des fonctions des variables réelles" , Gauthier-Villars (1937) |
Differential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential&oldid=13451