Difference between revisions of "Differential"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | d0318101.png | ||
| + | $#A+1 = 161 n = 0 | ||
| + | $#C+1 = 161 : ~/encyclopedia/old_files/data/D031/D.0301810 Differential | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
The main linear part of increment of a function. | The main linear part of increment of a function. | ||
| − | 1) A real-valued function | + | 1) A real-valued function $ f $ |
| + | of a real variable $ x $ | ||
| + | is said to be differentiable at a point $ x $ | ||
| + | if it is defined in some neighbourhood of this point and if there exists a number $ A $ | ||
| + | such that the increment | ||
| − | + | $$ | |
| + | \Delta y = f ( x + \Delta x ) - f ( x) | ||
| + | $$ | ||
| − | may be written (if the point | + | may be written (if the point $ x + \Delta x $ |
| + | lies in this neighbourhood) in the form | ||
| − | + | $$ | |
| + | \Delta y = A \Delta x + \omega , | ||
| + | $$ | ||
| − | where | + | where $ \omega / \Delta x \rightarrow 0 $ |
| + | as $ \Delta x \rightarrow 0 $. | ||
| + | Here $ A \Delta x $ | ||
| + | is usually denoted by $ dy $ | ||
| + | and is called the differential of $ f $ | ||
| + | at $ x $. | ||
| + | For a given $ x $ | ||
| + | the differential $ dy $ | ||
| + | is proportional to $ \Delta x $, | ||
| + | i.e. is a linear function of $ \Delta x $. | ||
| + | By definition, as $ \Delta x \rightarrow 0 $ | ||
| + | the additional term $ \omega $ | ||
| + | is infinitely small of a higher order than $ \Delta x $( | ||
| + | and also than $ dy $ | ||
| + | if $ A \neq 0 $). | ||
| + | This is why the differential is said to be the main part of increment of the function. | ||
| − | For a function which is differentiable at a point | + | For a function which is differentiable at a point $ x $, |
| + | $ \Delta y \rightarrow 0 $ | ||
| + | if $ \Delta x \rightarrow 0 $, | ||
| + | i.e. a function which is differentiable at a point is continuous at that point. A function $ f $ | ||
| + | is differentiable at a point $ x $ | ||
| + | if and only if it has, at that point, a finite derivative | ||
| − | + | $$ | |
| + | f ^ { \prime } ( x) = \lim\limits _ {\Delta x \rightarrow 0 } \ | ||
| + | |||
| + | \frac{\Delta y }{\Delta x } | ||
| + | = A ; | ||
| + | $$ | ||
moreover, | moreover, | ||
| − | + | $$ | |
| + | d y = f ^ { \prime } ( x) \Delta x . | ||
| + | $$ | ||
There exist continuous functions which are not differentiable. | There exist continuous functions which are not differentiable. | ||
| − | The designation | + | The designation $ df ( x) $ |
| + | may be used instead of $ dy $, | ||
| + | and the above equation assumes the form | ||
| − | + | $$ | |
| + | d f ( x) = f ^ { \prime } ( x) \Delta x . | ||
| + | $$ | ||
| − | The increment of the argument | + | The increment of the argument $ \Delta x $ |
| + | is then usually denoted by $ dx $, | ||
| + | and is said to be the differential of the independent variable. Accordingly, one may write | ||
| − | + | $$ | |
| + | d y = f ^ { \prime } ( x) d x . | ||
| + | $$ | ||
| − | Hence | + | Hence $ f ^ { \prime } ( x) = dy / dx $, |
| + | i.e. the derivative is equal to the ratio of the differentials $ dy $ | ||
| + | and $ dx $. | ||
| + | If $ A \neq 0 $, | ||
| + | then $ \Delta y / dy \rightarrow 1 $ | ||
| + | as $ \Delta x \rightarrow 0 $, | ||
| + | i.e. if $ A \neq 0 $, | ||
| + | then $ \Delta y $ | ||
| + | and $ dy $ | ||
| + | are infinitesimals of the same order as $ \Delta x \rightarrow 0 $; | ||
| + | this fact, along with the simple structure of the differential (i.e. linearity with respect to $ \Delta x $), | ||
| + | is often used in approximate computations, by assuming that $ \Delta y \approx dy $ | ||
| + | for small $ \Delta x $. | ||
| + | E.g., if it is desired to compute $ f ( x + \Delta x ) $ | ||
| + | from a known $ f ( x) $ | ||
| + | when $ \Delta x $ | ||
| + | is small, it is assumed that | ||
| − | + | $$ | |
| + | f ( x + \Delta x ) \approx f( x) + dy . | ||
| + | $$ | ||
Obviously, such reasoning is useful only if it is possible to estimate the magnitude of the error involved. | Obviously, such reasoning is useful only if it is possible to estimate the magnitude of the error involved. | ||
| − | Geometric interpretation of the differential. The equation of the tangent to the graph of a function | + | Geometric interpretation of the differential. The equation of the tangent to the graph of a function $ f $ |
| + | at a point $ ( x _ {0} , y _ {0} ) $ | ||
| + | is of the form $ y - y _ {0} = f ^ { \prime } ( x _ {0} ) ( x - x _ {0} ) $. | ||
| + | If one puts $ x = x _ {0} + \Delta x $, | ||
| + | then $ y - y _ {0} = f ^ { \prime } ( x _ {0} ) \Delta x $. | ||
| + | The right-hand side represents the value of the differential of the function $ f $ | ||
| + | at the point $ x _ {0} $ | ||
| + | corresponding to the value of $ \Delta x $ | ||
| + | being considered. Thus, the differential is identical with the corresponding increment of the ordinate of the tangent to the curve $ y = f ( x) $( | ||
| + | cf. the segment $ NT $ | ||
| + | in Fig. a). Here $ \omega = \Delta y - dy $, | ||
| + | i.e. the value of $ | \omega | $ | ||
| + | coincides with the length of the segment $ TS $. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d031810a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d031810a.gif" /> | ||
| Line 41: | Line 127: | ||
Figure: d031810a | Figure: d031810a | ||
| − | 2) The definitions of differentiability and differential are readily extended to real-valued functions of | + | 2) The definitions of differentiability and differential are readily extended to real-valued functions of $ n $ |
| + | real variables. Thus, in the case $ n = 2 $ | ||
| + | a real-valued function is said to be differentiable at a point $ ( x , y ) $ | ||
| + | with respect to both variables $ x $ | ||
| + | and $ y $ | ||
| + | if it is defined in some neighbourhood of this point and if its total increment | ||
| − | + | $$ | |
| + | \Delta z = f ( x + \Delta x , y + \Delta y ) - f ( x , y ) | ||
| + | $$ | ||
may be written as | may be written as | ||
| − | + | $$ | |
| + | \Delta z = A \Delta x + B \Delta y + \alpha , | ||
| + | $$ | ||
| − | where | + | where $ A $ |
| + | and $ B $ | ||
| + | are real numbers, $ \alpha / \rho \rightarrow 0 $ | ||
| + | if $ \rho \rightarrow 0 $, | ||
| + | $ \rho = \sqrt {\Delta x ^ {2} + \Delta y ^ {2} } $; | ||
| + | it is assumed that the point $ ( x + \Delta x , y + \Delta y ) $ | ||
| + | belongs to the neighbourhood mentioned above (Fig. b). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d031810b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d031810b.gif" /> | ||
| Line 57: | Line 158: | ||
One introduces the notation | One introduces the notation | ||
| − | + | $$ | |
| + | d z = d f ( x , y ) = A \Delta x + B \Delta y; | ||
| + | $$ | ||
| − | + | $ dz $ | |
| + | is said to be the total differential, or simply the differential, of the function $ f $ | ||
| + | at the point $ ( x , y ) $( | ||
| + | the phrase "with respect to both variables x and y" is sometimes added). For a given point $ ( x , y ) $ | ||
| + | the differential $ dz $ | ||
| + | is a linear function of $ \Delta x $ | ||
| + | and $ \Delta y $; | ||
| + | the difference $ \alpha = \Delta z - dz $ | ||
| + | is infinitely small of a higher order than $ \rho $. | ||
| + | In this sense $ dz $ | ||
| + | is the main linear part of the increment $ \Delta z $. | ||
| − | If | + | If $ f $ |
| + | is differentiable at the point $ ( x , y ) $, | ||
| + | then it is continuous at this point and has finite partial derivatives (cf. [[Derivative|Derivative]]) | ||
| − | + | $$ | |
| + | f _ {x} ^ { \prime } ( x , y ) = A ,\ \ | ||
| + | f _ {y} ^ { \prime } ( x , y ) = B | ||
| + | $$ | ||
at this point. Thus | at this point. Thus | ||
| − | + | $$ | |
| + | d z = d f ( x , y ) = f _ {x} ^ { \prime } ( x , y ) | ||
| + | \Delta x + f _ {y} ^ { \prime } ( x , y ) \Delta y . | ||
| + | $$ | ||
| − | The increments | + | The increments $ \Delta x $ |
| + | and $ \Delta y $ | ||
| + | of the independent variables are usually denoted by $ dy $ | ||
| + | and $ dx $, | ||
| + | as in the case of a single variable. One may write, accordingly, | ||
| − | + | $$ | |
| + | d z = d f ( x , y ) = f _ {x} ^ { \prime } ( x , y ) | ||
| + | d x + f _ {y} ^ { \prime } ( x , y ) d y . | ||
| + | $$ | ||
The existence of finite partial derivatives does not, in general, entail the differentiability of the function (even if it is assumed to be continuous). | The existence of finite partial derivatives does not, in general, entail the differentiability of the function (even if it is assumed to be continuous). | ||
| − | If a function | + | If a function $ f $ |
| + | has a partial derivative with respect to $ x $ | ||
| + | at a point $ ( x , y ) $, | ||
| + | the product $ f _ {x} ^ { \prime } ( x , y ) dx $ | ||
| + | is said to be its partial differential with respect to $ x $; | ||
| + | in the same manner, $ f _ {y} ^ { \prime } ( x , y ) dy $ | ||
| + | is the partial differential with respect to $ y $. | ||
| + | If the function is differentiable, its total differential is equal to the sum of the partial differentials. Geometrically, the total differential $ df ( x _ {0} , y _ {0} ) $ | ||
| + | is the increment in the $ z $- | ||
| + | direction in the tangent plane to the surface $ z = f ( x , y ) $ | ||
| + | at the point $ ( x _ {0} , y _ {0} , z _ {0} ) $, | ||
| + | where $ z _ {0} = f ( x _ {0} , y _ {0} ) $( | ||
| + | Fig. c). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d031810c.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d031810c.gif" /> | ||
| Line 81: | Line 221: | ||
Figure: d031810c | Figure: d031810c | ||
| − | The following is a sufficient criterion for the differentiability of a function: If in a certain neighbourhood of a point | + | The following is a sufficient criterion for the differentiability of a function: If in a certain neighbourhood of a point $ ( x _ {0} , y _ {0} ) $ |
| + | a function $ f $ | ||
| + | has a partial derivative $ f _ {x} ^ { \prime } $ | ||
| + | which is continuous at $ ( x _ {0} , y _ {0} ) $ | ||
| + | and, in addition, has a partial derivative $ f _ {y} ^ { \prime } $ | ||
| + | at that point, then $ f $ | ||
| + | is differentiable at that point. | ||
| − | If a function | + | If a function $ f $ |
| + | is differentiable at all points of an open domain $ D $, | ||
| + | then at any point of the domain | ||
| − | + | $$ | |
| + | d z = A ( x , y ) d x + B ( x , y ) d y , | ||
| + | $$ | ||
| − | where | + | where $ A ( x , y ) = f _ {x} ^ { \prime } ( x , y ) $, |
| + | $ B ( x , y ) = f _ {y} ^ { \prime } ( x , y ) $. | ||
| + | If, in addition, there exist continuous partial derivatives $ A _ {y} ^ \prime $ | ||
| + | and $ B _ {x} ^ { \prime } $ | ||
| + | in $ D $, | ||
| + | then, everywhere in $ D $, | ||
| − | + | $$ | |
| + | A _ {y} ^ \prime = B _ {x} ^ { \prime } . | ||
| + | $$ | ||
This proves, in particular, that not every expression | This proves, in particular, that not every expression | ||
| − | + | $$ | |
| + | A ( x , y ) d x + B ( x , y ) d y | ||
| + | $$ | ||
| − | with continuous | + | with continuous $ A $ |
| + | and $ B $( | ||
| + | in a domain $ D $) | ||
| + | is the total differential of some function of two variables. This is a difference from functions of one variable, where any expression $ A ( x) d x $ | ||
| + | with a continuous function $ A $ | ||
| + | in some interval is the differential of some function. | ||
| − | The expression | + | The expression $ A dx + B dy $ |
| + | is the total differential of some function $ z = f ( x , y ) $ | ||
| + | in a simply-connected open domain $ D $ | ||
| + | if $ A $ | ||
| + | and $ B $ | ||
| + | are continuous in this domain, meet the condition $ A _ {y} ^ \prime = B _ {x} ^ { \prime } $ | ||
| + | and, in addition: a) $ A _ {y} ^ \prime $ | ||
| + | and $ B _ {x} ^ { \prime } $ | ||
| + | are continuous or b) $ A $ | ||
| + | and $ B $ | ||
| + | are everywhere differentiable in $ D $ | ||
| + | with respect to both variables $ x $ | ||
| + | and $ y $[[#References|[7]]], [[#References|[8]]]. | ||
See also [[Differential calculus|Differential calculus]] for differentials of real-valued functions of one or more real variables and for differentials of higher orders. | See also [[Differential calculus|Differential calculus]] for differentials of real-valued functions of one or more real variables and for differentials of higher orders. | ||
| − | 3) Let a function | + | 3) Let a function $ f $ |
| + | be defined on some set $ E $ | ||
| + | of real numbers, let $ x $ | ||
| + | be a limit point of this set, let $ x \in E $, | ||
| + | $ x + \Delta x \in E $, | ||
| + | $ \Delta y = A \Delta x + \alpha $, | ||
| + | where $ \alpha / \Delta x \rightarrow 0 $ | ||
| + | if $ \Delta x \rightarrow 0 $; | ||
| + | then the function $ f $ | ||
| + | is called differentiable with respect to the set $ E $ | ||
| + | at $ x $, | ||
| + | while $ dy = A \Delta x $ | ||
| + | is called its differential with respect to the set $ E $ | ||
| + | at $ x $. | ||
| + | This is a generalization of the differential of a real-valued function of one real variable. Special kinds of this generalization include differentials at the end points of the interval within which the function is defined, and the approximate differential (cf. [[Approximate differentiability|Approximate differentiability]]). | ||
Differentials with respect to a set for real-valued functions of several real variables are introduced in a similar manner. | Differentials with respect to a set for real-valued functions of several real variables are introduced in a similar manner. | ||
| Line 109: | Line 299: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.P. Tolstov, "Elements of mathematical analysis" , '''1–2''' , Moscow (1974) (In Russian) {{MR|0357695}} {{MR|0354961}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G.M. Fichtenholz, "Differential und Integralrechnung" , '''1''' , Deutsch. Verlag Wissenschaft. (1964) {{MR|1191905}} {{MR|1056870}} {{MR|1056869}} {{MR|0887101}} {{MR|0845556}} {{MR|0845555}} {{MR|0524565}} {{MR|0473117}} {{MR|0344040}} {{MR|0344039}} {{MR|0238635}} {{MR|0238637}} {{MR|0238636}} {{ZBL|0143.27002}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> L.D. Kudryavtsev, "Mathematical analysis" , '''1''' , Moscow (1973) (In Russian) {{MR|1617334}} {{MR|1070567}} {{MR|1070566}} {{MR|1070565}} {{MR|0866891}} {{MR|0767983}} {{MR|0767982}} {{MR|0628614}} {{MR|0619214}} {{ZBL|1080.00002}} {{ZBL|1080.00001}} {{ZBL|1060.26002}} {{ZBL|0869.00003}} {{ZBL|0696.26002}} {{ZBL|0703.26001}} {{ZBL|0609.00001}} {{ZBL|0632.26001}} {{ZBL|0485.26002}} {{ZBL|0485.26001}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.M. Nikol'skii, "A course of mathematical analysis" , '''1''' , MIR (1977) (Translated from Russian) {{MR|}} {{ZBL|0397.00003}} {{ZBL|0384.00004}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) {{MR|0055409}} {{ZBL|0052.05301}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , '''1–2''' , Graylock (1957–1961) (Translated from Russian) {{MR|1025126}} {{MR|0708717}} {{MR|0630899}} {{MR|0435771}} {{MR|0377444}} {{MR|0234241}} {{MR|0215962}} {{MR|0118796}} {{MR|1530727}} {{MR|0118795}} {{MR|0085462}} {{MR|0070045}} {{ZBL|0932.46001}} {{ZBL|0672.46001}} {{ZBL|0501.46001}} {{ZBL|0501.46002}} {{ZBL|0235.46001}} {{ZBL|0103.08801}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> G.P. Tolstov, "On curvilinear and iterated integrals" ''Trudy Mat. Inst. Steklov.'' , '''35''' (1950) (In Russian) {{MR|44612}} {{ZBL|}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> G.P. Tolstov, "On the total differential" ''Uspekhi Mat. Nauk'' , '''3''' : 5 (1948) pp. 167–170 {{MR|0027044}} {{ZBL|}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.P. Tolstov, "Elements of mathematical analysis" , '''1–2''' , Moscow (1974) (In Russian) {{MR|0357695}} {{MR|0354961}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G.M. Fichtenholz, "Differential und Integralrechnung" , '''1''' , Deutsch. Verlag Wissenschaft. (1964) {{MR|1191905}} {{MR|1056870}} {{MR|1056869}} {{MR|0887101}} {{MR|0845556}} {{MR|0845555}} {{MR|0524565}} {{MR|0473117}} {{MR|0344040}} {{MR|0344039}} {{MR|0238635}} {{MR|0238637}} {{MR|0238636}} {{ZBL|0143.27002}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> L.D. Kudryavtsev, "Mathematical analysis" , '''1''' , Moscow (1973) (In Russian) {{MR|1617334}} {{MR|1070567}} {{MR|1070566}} {{MR|1070565}} {{MR|0866891}} {{MR|0767983}} {{MR|0767982}} {{MR|0628614}} {{MR|0619214}} {{ZBL|1080.00002}} {{ZBL|1080.00001}} {{ZBL|1060.26002}} {{ZBL|0869.00003}} {{ZBL|0696.26002}} {{ZBL|0703.26001}} {{ZBL|0609.00001}} {{ZBL|0632.26001}} {{ZBL|0485.26002}} {{ZBL|0485.26001}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.M. Nikol'skii, "A course of mathematical analysis" , '''1''' , MIR (1977) (Translated from Russian) {{MR|}} {{ZBL|0397.00003}} {{ZBL|0384.00004}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) {{MR|0055409}} {{ZBL|0052.05301}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , '''1–2''' , Graylock (1957–1961) (Translated from Russian) {{MR|1025126}} {{MR|0708717}} {{MR|0630899}} {{MR|0435771}} {{MR|0377444}} {{MR|0234241}} {{MR|0215962}} {{MR|0118796}} {{MR|1530727}} {{MR|0118795}} {{MR|0085462}} {{MR|0070045}} {{ZBL|0932.46001}} {{ZBL|0672.46001}} {{ZBL|0501.46001}} {{ZBL|0501.46002}} {{ZBL|0235.46001}} {{ZBL|0103.08801}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> G.P. Tolstov, "On curvilinear and iterated integrals" ''Trudy Mat. Inst. Steklov.'' , '''35''' (1950) (In Russian) {{MR|44612}} {{ZBL|}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> G.P. Tolstov, "On the total differential" ''Uspekhi Mat. Nauk'' , '''3''' : 5 (1948) pp. 167–170 {{MR|0027044}} {{ZBL|}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| Line 119: | Line 307: | ||
For generalizations to functions between abstract spaces see also [[Fréchet derivative|Fréchet derivative]]; [[Gâteaux derivative|Gâteaux derivative]]. | For generalizations to functions between abstract spaces see also [[Fréchet derivative|Fréchet derivative]]; [[Gâteaux derivative|Gâteaux derivative]]. | ||
| − | For the derivative of a function | + | For the derivative of a function $ f : \mathbf C \rightarrow \mathbf C $ |
| + | see [[Analytic function|Analytic function]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T.M. Apostol, "Calculus" , '''1–2''' , Blaisdell (1964) {{MR|1908007}} {{MR|1182316}} {{MR|1182315}} {{MR|0595410}} {{MR|1536963}} {{MR|1535772}} {{MR|0271732}} {{MR|0248290}} {{MR|0247001}} {{MR|0261376}} {{MR|0250092}} {{MR|0236734}} {{MR|0236733}} {{MR|0214705}} {{MR|1532185}} {{MR|1531712}} {{MR|0087718}} {{ZBL|0123.25902}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1974) {{MR|0344384}} {{ZBL|0309.26002}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Fleming, "Functions of several variables" , Springer (1977) {{MR|0422527}} {{ZBL|0348.26002}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) {{MR|0604364}} {{ZBL|0454.26001}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R. Courant, "Vorlesungen über Differential- und Integralrechnung" , '''1–2''' , Springer (1971–1972) {{MR|0190266}} {{MR|1521849}} {{MR|1521664}} {{ZBL|0224.26001}} {{ZBL|0217.37201}} {{ZBL|0121.28904}} {{ZBL|0066.30303}} {{ZBL|0064.04704}} {{ZBL|0003.05401}} {{ZBL|57.0246.01}} {{ZBL|56.0193.01}} {{ZBL|53.0200.13}} {{ZBL|55.0728.02}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian) {{MR|0640867}} {{MR|0409747}} {{MR|0259033}} {{MR|0063424}} {{ZBL|0097.26601}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> G.E. Shilov, B.L. Gurevich, "Integral, measure, and derivative: a unified approach" , Dover, reprint (1977) (Translated from Russian) {{MR|0466463}} {{ZBL|0391.28007}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> A. Denjoy, "Introduction à la théorie des fonctions des variables réelles" , Gauthier-Villars (1937) {{MR|}} {{ZBL|0017.10504}} {{ZBL|63.0177.02}} {{ZBL|63.0177.01}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T.M. Apostol, "Calculus" , '''1–2''' , Blaisdell (1964) {{MR|1908007}} {{MR|1182316}} {{MR|1182315}} {{MR|0595410}} {{MR|1536963}} {{MR|1535772}} {{MR|0271732}} {{MR|0248290}} {{MR|0247001}} {{MR|0261376}} {{MR|0250092}} {{MR|0236734}} {{MR|0236733}} {{MR|0214705}} {{MR|1532185}} {{MR|1531712}} {{MR|0087718}} {{ZBL|0123.25902}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1974) {{MR|0344384}} {{ZBL|0309.26002}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Fleming, "Functions of several variables" , Springer (1977) {{MR|0422527}} {{ZBL|0348.26002}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) {{MR|0604364}} {{ZBL|0454.26001}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R. Courant, "Vorlesungen über Differential- und Integralrechnung" , '''1–2''' , Springer (1971–1972) {{MR|0190266}} {{MR|1521849}} {{MR|1521664}} {{ZBL|0224.26001}} {{ZBL|0217.37201}} {{ZBL|0121.28904}} {{ZBL|0066.30303}} {{ZBL|0064.04704}} {{ZBL|0003.05401}} {{ZBL|57.0246.01}} {{ZBL|56.0193.01}} {{ZBL|53.0200.13}} {{ZBL|55.0728.02}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian) {{MR|0640867}} {{MR|0409747}} {{MR|0259033}} {{MR|0063424}} {{ZBL|0097.26601}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> G.E. Shilov, B.L. Gurevich, "Integral, measure, and derivative: a unified approach" , Dover, reprint (1977) (Translated from Russian) {{MR|0466463}} {{ZBL|0391.28007}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> A. Denjoy, "Introduction à la théorie des fonctions des variables réelles" , Gauthier-Villars (1937) {{MR|}} {{ZBL|0017.10504}} {{ZBL|63.0177.02}} {{ZBL|63.0177.01}} </TD></TR></table> | ||
Revision as of 17:33, 5 June 2020
The main linear part of increment of a function.
1) A real-valued function $ f $ of a real variable $ x $ is said to be differentiable at a point $ x $ if it is defined in some neighbourhood of this point and if there exists a number $ A $ such that the increment
$$ \Delta y = f ( x + \Delta x ) - f ( x) $$
may be written (if the point $ x + \Delta x $ lies in this neighbourhood) in the form
$$ \Delta y = A \Delta x + \omega , $$
where $ \omega / \Delta x \rightarrow 0 $ as $ \Delta x \rightarrow 0 $. Here $ A \Delta x $ is usually denoted by $ dy $ and is called the differential of $ f $ at $ x $. For a given $ x $ the differential $ dy $ is proportional to $ \Delta x $, i.e. is a linear function of $ \Delta x $. By definition, as $ \Delta x \rightarrow 0 $ the additional term $ \omega $ is infinitely small of a higher order than $ \Delta x $( and also than $ dy $ if $ A \neq 0 $). This is why the differential is said to be the main part of increment of the function.
For a function which is differentiable at a point $ x $, $ \Delta y \rightarrow 0 $ if $ \Delta x \rightarrow 0 $, i.e. a function which is differentiable at a point is continuous at that point. A function $ f $ is differentiable at a point $ x $ if and only if it has, at that point, a finite derivative
$$ f ^ { \prime } ( x) = \lim\limits _ {\Delta x \rightarrow 0 } \ \frac{\Delta y }{\Delta x } = A ; $$
moreover,
$$ d y = f ^ { \prime } ( x) \Delta x . $$
There exist continuous functions which are not differentiable.
The designation $ df ( x) $ may be used instead of $ dy $, and the above equation assumes the form
$$ d f ( x) = f ^ { \prime } ( x) \Delta x . $$
The increment of the argument $ \Delta x $ is then usually denoted by $ dx $, and is said to be the differential of the independent variable. Accordingly, one may write
$$ d y = f ^ { \prime } ( x) d x . $$
Hence $ f ^ { \prime } ( x) = dy / dx $, i.e. the derivative is equal to the ratio of the differentials $ dy $ and $ dx $. If $ A \neq 0 $, then $ \Delta y / dy \rightarrow 1 $ as $ \Delta x \rightarrow 0 $, i.e. if $ A \neq 0 $, then $ \Delta y $ and $ dy $ are infinitesimals of the same order as $ \Delta x \rightarrow 0 $; this fact, along with the simple structure of the differential (i.e. linearity with respect to $ \Delta x $), is often used in approximate computations, by assuming that $ \Delta y \approx dy $ for small $ \Delta x $. E.g., if it is desired to compute $ f ( x + \Delta x ) $ from a known $ f ( x) $ when $ \Delta x $ is small, it is assumed that
$$ f ( x + \Delta x ) \approx f( x) + dy . $$
Obviously, such reasoning is useful only if it is possible to estimate the magnitude of the error involved.
Geometric interpretation of the differential. The equation of the tangent to the graph of a function $ f $ at a point $ ( x _ {0} , y _ {0} ) $ is of the form $ y - y _ {0} = f ^ { \prime } ( x _ {0} ) ( x - x _ {0} ) $. If one puts $ x = x _ {0} + \Delta x $, then $ y - y _ {0} = f ^ { \prime } ( x _ {0} ) \Delta x $. The right-hand side represents the value of the differential of the function $ f $ at the point $ x _ {0} $ corresponding to the value of $ \Delta x $ being considered. Thus, the differential is identical with the corresponding increment of the ordinate of the tangent to the curve $ y = f ( x) $( cf. the segment $ NT $ in Fig. a). Here $ \omega = \Delta y - dy $, i.e. the value of $ | \omega | $ coincides with the length of the segment $ TS $.
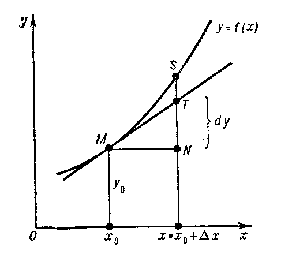
Figure: d031810a
2) The definitions of differentiability and differential are readily extended to real-valued functions of $ n $ real variables. Thus, in the case $ n = 2 $ a real-valued function is said to be differentiable at a point $ ( x , y ) $ with respect to both variables $ x $ and $ y $ if it is defined in some neighbourhood of this point and if its total increment
$$ \Delta z = f ( x + \Delta x , y + \Delta y ) - f ( x , y ) $$
may be written as
$$ \Delta z = A \Delta x + B \Delta y + \alpha , $$
where $ A $ and $ B $ are real numbers, $ \alpha / \rho \rightarrow 0 $ if $ \rho \rightarrow 0 $, $ \rho = \sqrt {\Delta x ^ {2} + \Delta y ^ {2} } $; it is assumed that the point $ ( x + \Delta x , y + \Delta y ) $ belongs to the neighbourhood mentioned above (Fig. b).
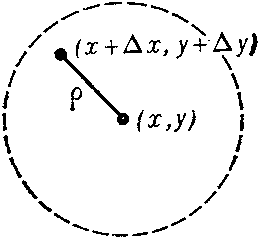
Figure: d031810b
One introduces the notation
$$ d z = d f ( x , y ) = A \Delta x + B \Delta y; $$
$ dz $ is said to be the total differential, or simply the differential, of the function $ f $ at the point $ ( x , y ) $( the phrase "with respect to both variables x and y" is sometimes added). For a given point $ ( x , y ) $ the differential $ dz $ is a linear function of $ \Delta x $ and $ \Delta y $; the difference $ \alpha = \Delta z - dz $ is infinitely small of a higher order than $ \rho $. In this sense $ dz $ is the main linear part of the increment $ \Delta z $.
If $ f $ is differentiable at the point $ ( x , y ) $, then it is continuous at this point and has finite partial derivatives (cf. Derivative)
$$ f _ {x} ^ { \prime } ( x , y ) = A ,\ \ f _ {y} ^ { \prime } ( x , y ) = B $$
at this point. Thus
$$ d z = d f ( x , y ) = f _ {x} ^ { \prime } ( x , y ) \Delta x + f _ {y} ^ { \prime } ( x , y ) \Delta y . $$
The increments $ \Delta x $ and $ \Delta y $ of the independent variables are usually denoted by $ dy $ and $ dx $, as in the case of a single variable. One may write, accordingly,
$$ d z = d f ( x , y ) = f _ {x} ^ { \prime } ( x , y ) d x + f _ {y} ^ { \prime } ( x , y ) d y . $$
The existence of finite partial derivatives does not, in general, entail the differentiability of the function (even if it is assumed to be continuous).
If a function $ f $ has a partial derivative with respect to $ x $ at a point $ ( x , y ) $, the product $ f _ {x} ^ { \prime } ( x , y ) dx $ is said to be its partial differential with respect to $ x $; in the same manner, $ f _ {y} ^ { \prime } ( x , y ) dy $ is the partial differential with respect to $ y $. If the function is differentiable, its total differential is equal to the sum of the partial differentials. Geometrically, the total differential $ df ( x _ {0} , y _ {0} ) $ is the increment in the $ z $- direction in the tangent plane to the surface $ z = f ( x , y ) $ at the point $ ( x _ {0} , y _ {0} , z _ {0} ) $, where $ z _ {0} = f ( x _ {0} , y _ {0} ) $( Fig. c).
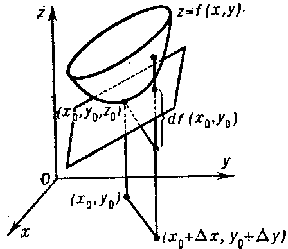
Figure: d031810c
The following is a sufficient criterion for the differentiability of a function: If in a certain neighbourhood of a point $ ( x _ {0} , y _ {0} ) $ a function $ f $ has a partial derivative $ f _ {x} ^ { \prime } $ which is continuous at $ ( x _ {0} , y _ {0} ) $ and, in addition, has a partial derivative $ f _ {y} ^ { \prime } $ at that point, then $ f $ is differentiable at that point.
If a function $ f $ is differentiable at all points of an open domain $ D $, then at any point of the domain
$$ d z = A ( x , y ) d x + B ( x , y ) d y , $$
where $ A ( x , y ) = f _ {x} ^ { \prime } ( x , y ) $, $ B ( x , y ) = f _ {y} ^ { \prime } ( x , y ) $. If, in addition, there exist continuous partial derivatives $ A _ {y} ^ \prime $ and $ B _ {x} ^ { \prime } $ in $ D $, then, everywhere in $ D $,
$$ A _ {y} ^ \prime = B _ {x} ^ { \prime } . $$
This proves, in particular, that not every expression
$$ A ( x , y ) d x + B ( x , y ) d y $$
with continuous $ A $ and $ B $( in a domain $ D $) is the total differential of some function of two variables. This is a difference from functions of one variable, where any expression $ A ( x) d x $ with a continuous function $ A $ in some interval is the differential of some function.
The expression $ A dx + B dy $ is the total differential of some function $ z = f ( x , y ) $ in a simply-connected open domain $ D $ if $ A $ and $ B $ are continuous in this domain, meet the condition $ A _ {y} ^ \prime = B _ {x} ^ { \prime } $ and, in addition: a) $ A _ {y} ^ \prime $ and $ B _ {x} ^ { \prime } $ are continuous or b) $ A $ and $ B $ are everywhere differentiable in $ D $ with respect to both variables $ x $ and $ y $[7], [8].
See also Differential calculus for differentials of real-valued functions of one or more real variables and for differentials of higher orders.
3) Let a function $ f $ be defined on some set $ E $ of real numbers, let $ x $ be a limit point of this set, let $ x \in E $, $ x + \Delta x \in E $, $ \Delta y = A \Delta x + \alpha $, where $ \alpha / \Delta x \rightarrow 0 $ if $ \Delta x \rightarrow 0 $; then the function $ f $ is called differentiable with respect to the set $ E $ at $ x $, while $ dy = A \Delta x $ is called its differential with respect to the set $ E $ at $ x $. This is a generalization of the differential of a real-valued function of one real variable. Special kinds of this generalization include differentials at the end points of the interval within which the function is defined, and the approximate differential (cf. Approximate differentiability).
Differentials with respect to a set for real-valued functions of several real variables are introduced in a similar manner.
4) All definitions of differentiability and a differential given above can be extended, almost unchanged, to complex-valued functions of one or more real variables; to real-valued and complex-valued vector-functions of one or more real variables; and to complex functions and vector-functions of one or more complex variables. In functional analysis they are extended to functions of the points of an abstract space. One may speak of differentiability and of the differential of a set function with respect to some measure.
References
| [1] | G.P. Tolstov, "Elements of mathematical analysis" , 1–2 , Moscow (1974) (In Russian) MR0357695 MR0354961 |
| [2] | G.M. Fichtenholz, "Differential und Integralrechnung" , 1 , Deutsch. Verlag Wissenschaft. (1964) MR1191905 MR1056870 MR1056869 MR0887101 MR0845556 MR0845555 MR0524565 MR0473117 MR0344040 MR0344039 MR0238635 MR0238637 MR0238636 Zbl 0143.27002 |
| [3] | L.D. Kudryavtsev, "Mathematical analysis" , 1 , Moscow (1973) (In Russian) MR1617334 MR1070567 MR1070566 MR1070565 MR0866891 MR0767983 MR0767982 MR0628614 MR0619214 Zbl 1080.00002 Zbl 1080.00001 Zbl 1060.26002 Zbl 0869.00003 Zbl 0696.26002 Zbl 0703.26001 Zbl 0609.00001 Zbl 0632.26001 Zbl 0485.26002 Zbl 0485.26001 |
| [4] | S.M. Nikol'skii, "A course of mathematical analysis" , 1 , MIR (1977) (Translated from Russian) Zbl 0397.00003 Zbl 0384.00004 |
| [5] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) MR0055409 Zbl 0052.05301 |
| [6] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) MR1025126 MR0708717 MR0630899 MR0435771 MR0377444 MR0234241 MR0215962 MR0118796 MR1530727 MR0118795 MR0085462 MR0070045 Zbl 0932.46001 Zbl 0672.46001 Zbl 0501.46001 Zbl 0501.46002 Zbl 0235.46001 Zbl 0103.08801 |
| [7] | G.P. Tolstov, "On curvilinear and iterated integrals" Trudy Mat. Inst. Steklov. , 35 (1950) (In Russian) MR44612 |
| [8] | G.P. Tolstov, "On the total differential" Uspekhi Mat. Nauk , 3 : 5 (1948) pp. 167–170 MR0027044 |
Comments
See also Differentiation; Differentiation of a mapping.
For differentiation of set functions cf. Set function; Radon–Nikodým theorem, [a7].
For generalizations to functions between abstract spaces see also Fréchet derivative; Gâteaux derivative.
For the derivative of a function $ f : \mathbf C \rightarrow \mathbf C $ see Analytic function.
References
| [a1] | T.M. Apostol, "Calculus" , 1–2 , Blaisdell (1964) MR1908007 MR1182316 MR1182315 MR0595410 MR1536963 MR1535772 MR0271732 MR0248290 MR0247001 MR0261376 MR0250092 MR0236734 MR0236733 MR0214705 MR1532185 MR1531712 MR0087718 Zbl 0123.25902 |
| [a2] | T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1974) MR0344384 Zbl 0309.26002 |
| [a3] | W. Fleming, "Functions of several variables" , Springer (1977) MR0422527 Zbl 0348.26002 |
| [a4] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) MR0604364 Zbl 0454.26001 |
| [a5] | R. Courant, "Vorlesungen über Differential- und Integralrechnung" , 1–2 , Springer (1971–1972) MR0190266 MR1521849 MR1521664 Zbl 0224.26001 Zbl 0217.37201 Zbl 0121.28904 Zbl 0066.30303 Zbl 0064.04704 Zbl 0003.05401 Zbl 57.0246.01 Zbl 56.0193.01 Zbl 53.0200.13 Zbl 55.0728.02 |
| [a6] | I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian) MR0640867 MR0409747 MR0259033 MR0063424 Zbl 0097.26601 |
| [a7] | G.E. Shilov, B.L. Gurevich, "Integral, measure, and derivative: a unified approach" , Dover, reprint (1977) (Translated from Russian) MR0466463 Zbl 0391.28007 |
| [a8] | A. Denjoy, "Introduction à la théorie des fonctions des variables réelles" , Gauthier-Villars (1937) Zbl 0017.10504 Zbl 63.0177.02 Zbl 63.0177.01 |
Differential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential&oldid=46660