Difference scheme
A system of difference equations (cf. Difference equation) approximating a differential equation and subsidiary (initial, boundary and other) conditions. Approximating an original differential problem by a difference scheme is one of the methods of approximating the original problem by a discrete problem. For this the given region 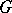 of independent variables is replaced by a discrete set of points
of independent variables is replaced by a discrete set of points 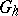 — the grid, and the derivatives entering into the differential equation are replaced by difference relations on the grid
— the grid, and the derivatives entering into the differential equation are replaced by difference relations on the grid  . As a result of such a change one obtains a closed system of a large number of algebraic equations (linear or non-linear, depending on the original differential equation) which makes up the difference scheme. In essence a difference scheme is a family of difference equations depending on the steps of the grid. The solution of a difference scheme also depends parametrically on the steps of the grid. A difference scheme is a multi-parameter and complicated object. Besides the coefficients of the original differential equation it contains also its own characteristic parameters, such as the steps with respect to time and space, weight factors, and others. The influence of these parameters can substantially distort the representation of the behaviour of the original differential problem.
. As a result of such a change one obtains a closed system of a large number of algebraic equations (linear or non-linear, depending on the original differential equation) which makes up the difference scheme. In essence a difference scheme is a family of difference equations depending on the steps of the grid. The solution of a difference scheme also depends parametrically on the steps of the grid. A difference scheme is a multi-parameter and complicated object. Besides the coefficients of the original differential equation it contains also its own characteristic parameters, such as the steps with respect to time and space, weight factors, and others. The influence of these parameters can substantially distort the representation of the behaviour of the original differential problem.
The following questions are being studied in connection with the approximation by difference schemes of differential equations: means of constructing a difference scheme; the convergence under grid refinement of the solution of the difference problem to the solution of the original differential equation; and methods for solving systems of difference equations. All the questions listed are considered in the theory of difference schemes (cf. Difference schemes, theory of). Effective numerical methods for solving typical difference schemes for ordinary and partial differential equations, assuming the use of a high-speed computer, have been developed.
A simple example of a difference scheme is given below. Suppose one is given the differential equation
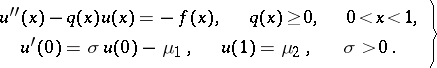 | (1) |
The domain 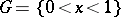 is replaced by the grid
is replaced by the grid
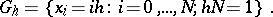 |
A difference scheme for problem (1) has the form
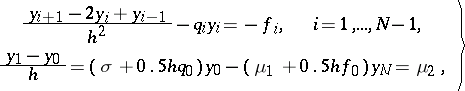 | (2) |
where 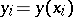 ,
, 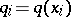 ,
, 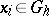 . It can be shown that, as
. It can be shown that, as 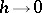 , the solution to the difference problem (2) converges to the solution of the original problem (1) for sufficiently smooth functions
, the solution to the difference problem (2) converges to the solution of the original problem (1) for sufficiently smooth functions 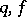 .
.
The difference scheme (2) has second-order accuracy, that is,
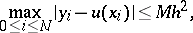 |
where 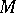 is a constant that does not depend on
is a constant that does not depend on 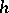 . The solution to the difference scheme (2) can be found by the shooting method.
. The solution to the difference scheme (2) can be found by the shooting method.
References
| [1] | A.A. Samarskii, "Theorie der Differenzverfahren" , Akad. Verlagsgesell. Geest u. Portig K.-D. (1984) (Translated from Russian) |
| [2] | A.A. Samarskii, E.S. Nikolaev, "Numerical methods for grid equations" , 1–2 , Birkhäuser (1989) (Translated from Russian) |
Comments
References
| [a1] | G.E. Forsythe, W.R. Wasow, "Finite difference methods for partial differential equations" , Wiley (1960) |
| [a2] | P.R. Garabedian, "Partial differential equations" , Wiley (1964) |
| [a3] | I. Gladwell (ed.) R. Wait (ed.) , A survey of numerical methods for partial differential equations , Clarendon Press (1979) |
| [a4] | A.R. Mitchell, D.F. Griffiths, "The finite difference method in partial differential equations" , Wiley (1980) |
| [a5] | R.D. Richtmeyer, K.W. Morton, "Difference methods for initial value problems" , Wiley (1967) |
| [a6] | G.D. Smith, "Numerical solution of partial differential equations" , Oxford Univ. Press (1977) |
| [a7] | N.N. Yanenko, "The method of fractional steps: solution of problems of mathematical physics in several variables" , Springer (1971) (Translated from Russian) |
Difference scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Difference_scheme&oldid=16045